1、二分查找

一、简介

  二分查找，也称为折半查找，是一种在有序数组中查找特定元素的高效算法。以下是二分查找的简介：

1.应用场景：

  二分查找主要用于那些已排序的数组或集合中，目的是快速找到目标元素或确定其是否存在。

2. 基本思想：

  二分查找的核心思想是通过不断将搜索范围减半来查找目标值。每次把目标值与中间元素比较，根据比较结果决定在左半部分还是右半部分继续查找。

3. 算法步骤：

  3.1、确保输入的数组是有序的。

  3.2、初始化两个索引，分别表示查找范围的开始和结束位置。

  3.3、计算中间索引，并获取中间元素的值。

  3.4、比较中间元素与目标值：

    3.4.1、如果相等，返回中间索引。
    3.4.2、如果目标值小于中间元素，更新结束索引为中间索引减一，缩小查找范围到左半部分。
    3.4.3、如果目标值大于中间元素，更新开始索引为中间索引加一，缩小查找范围到右半部分。
    3.4.4、重复上述步骤，直到找到目标值或开始索引大于结束索引（开始索引大于结束索引表示目标值不存在于数组中）。

4. 时间复杂度：

  二分查找的时间复杂度在平均和最坏情况下均为O(log n)，其中n是数组的长度。这是因为每次比较都能将搜索范围缩小一半。通过利用有序数据的特点，二分查找能够在大规模数据中实现快速查找，是计算机科学中一种非常重要的搜索算法。

二、代码实操：

1、java代码实现

public class Test {

    /**
     * 二分查找
     * 在数组array中查找目标值target，找到返回目标值索引，否则返回-1
     *
     * @param array  数组
     * @param target 需要查找的目标值
     * @return 目标值的索引位置，没有找到则返回-1
     */
    public static int binarySearch(int[] array, int target) {
        int i = 0; //开始索引
        int j = array.length - 1; //结束索引
        while (i <= j) {
            //m表示中间值索引，获取数组的中间值索引(向下取整。如：5/2=2.5,向下取整为2)；
            //int m=(i+j)/2;
            int m = (i + j) >>> 1; //这个方法相当于将 "(i + j)/2，这种方法叫做无符号右移一位"。

            //如果目标值大于中间元素，更新开始指针为中间索引加一，缩小查找范围到右半部分。
            if (target > array[m]) {
                i = m + 1;
                //如果目标值大于中间元素，更新开始索引为中间索引加一，缩小查找范围到右半部分。
            } else if (target < array[m]) {
                j = m - 1;
            } else {
                return m;
            }
        }
        return -1;
    }

    /**
     * 测试运行
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {7, 14, 21, 28, 35, 42, 49, 56};
        int m1 = binarySearch(a, 42);
        System.out.println("输出目标值索引为：" + m1);//输出目标值索引为：5

        int m2 = binarySearch(a, 66);
        System.out.println("输出目标值索引为：" + m2);//输出目标值索引为：-1
    }
}

2、疑问解答

问题1：while(i<=j) 循环条件为什么是 i<=j 而不是 i<j ?

  因为查找的目标值有可能是开始索引或者是结束索引。如果只用只有小于，那么会导致直接进入不了循环。比如查找的值是数组中的第一个值。或者数组中的值只有一个。那么开始索引和结束索引都是0 那么会导致进入不了循环。

问题1：为什么不能用 【int m=(i+j)/2；】 而是 【int m = (i + j) >>> 1;】?

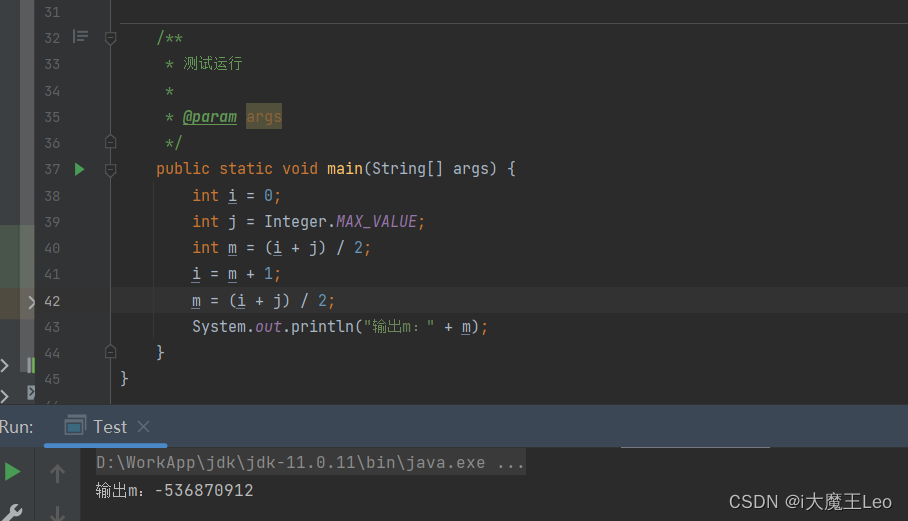
1. 避免整数溢出：
   当 “i + j” 的结果超过整数的最大值时，可能会发生整数溢出，出现负数（索引不能为负数）。这种情况下，直接进行除以2的操作可能得到错误的结果。而使用无符号右移一位 “(i + j) >>> 1” 相当于除以2并向下取整，且不会导致溢出问题。
     

2. 性能考虑：
   在某些编程语言和环境中，位运算（如无符号右移）的执行速度可能比除法运算更快。虽然这个差异在现代硬件和编译器优化下可能变得不明显，但在一些对性能要求较高的场景中，使用位运算可能会带来微小的性能优势。

3. 算法传统和一致性：
   使用无符号右移一位来计算中间索引是二分查找算法的一种传统实现方式，许多教材和代码示例都采用这种方法。这使得代码更具可读性和一致性，其他程序员在阅读和理解代码时更容易识别其为二分查找算法。

  总的来说，虽然 “int m = (i + j) / 2;” 在大多数情况下也能正常工作，但使用 “int m = (i + j) >>> 1;” 可以避免潜在的整数溢出问题，可能提供更好的性能，并与二分查找算法的传统实现保持一致。在实际编程中，可以根据具体需求和环境选择合适的实现方式。

3、二分查找怎么处理重复元素

3.1、如果一个数组中，被查找的值存在多个相同的值。如何找到最左边那个值。

3.1.1、改动的点：

1. 初始化候选变量candidate ，值为 -1，表示尚未找到目标值；
2. 如果目标值等于中间元素，将候选位置 candidate 设置为当前中间索引 m，表示找到了目标值。同时，将结束索引 j 更新为 m - 1，以便在下一次循环中检查更左侧的元素，从而找到最左边的相同元素。
3. 最后，返回候选位置 candidate。如果目标值存在于数组中，candidate 将是其最左边出现的位置；否则，candidate 将为 -1，表示目标值不在数组中。

public class Test {
    /**
     * 二分查找，在数组array中查找目标值target
     * 找相同值中的最左边一个
     *
     * @param array  数组
     * @param target 需要查找的目标值
     * @return 目标值的索引位置，没有找到则返回-1
     */
    public static int leftmost(int[] array, int target) {
        int i = 0;
        int j = array.length - 1;
        int candidate = -1; //1、创建一个候选存储值。
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target > array[m]) {
                i = m + 1;
            } else if (target < array[m]) {
                j = m - 1;
            } else {
                //2、如果目标值等于中间元素，将候选位置 candidate 设置为当前中间索引 m，表示找到了目标值。同时，将结束索引 j 更新为 m -1，以便在下一次循环中检查更左侧的元素，从而找到最左边的相同元素。
                candidate = m;
                j = m - 1;
            }
        }
        return candidate; //3、最后返回候选存储值。
    }

    /**
     * 测试运行
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {7, 14, 28, 28, 28, 28, 35, 42, 49, 56};
        int candidate = leftmost(a, 28);
        System.out.println("最左边值的索引是：" + candidate);//最左边值的索引是：2
    }
}

3.2、如果一个数组中，被查找的值存在多个相同的值。如何找到最右边那个值。

3.2.1、改动的点：

1. 初始化候选变量candidate ，值为 -1，表示尚未找到目标值；
2. 如果目标值等于中间元素，将候选位置 candidate 设置为当前中间索引 m，表示找到了目标值。同时，将开始索引 i 更新为 m + 1，以便在下一次循环中检查更右侧的元素，从而找到最右侧的相同元素。
3. 最后，返回候选位置 candidate。如果目标值存在于数组中，candidate 将是其最左边出现的位置；否则，candidate 将为 -1，表示目标值不在数组中。

    /**
     * 二分查找，在数组array中查找目标值target
     * 找相同值中的最右边一个
     *
     * @param array  数组
     * @param target 需要查找的目标值
     * @return 目标值的索引位置，没有找到则返回-1
     */
    public static int rightmost(int[] array, int target) {
        int i = 0;
        int j = array.length - 1;
        int candidate = -1; //1、创建一个候选存储值。
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target > array[m]) {
                i = m + 1;
            } else if (target < array[m]) {
                j = m - 1;
            } else {
                //2、如果目标值等于中间元素，将候选位置 candidate 设置为当前中间索引 m，表示找到了目标值。同时，将开始索引 i 更新为 m+1，以便在下一次循环中检查更右侧的元素，从而找到最右侧的相同元素。
                candidate = m;
                i = m + 1;
            }
        }
        return candidate; //3、最右边值的索引是：5
    }

    /**
     * 测试运行
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {7, 14, 28, 28, 28, 28, 35, 42, 49, 56};
        int candidate = rightmost(a, 28);
        System.out.println("最右边值的索引是：" + candidate);//最右边值的索引是：5
    }

三、其他场景应用代码改动版

1. 如何获取一个元素的最左侧位置，如果没有该元素，则返回该元素 的插入位置。
   代码

public class Test2 {

    /**
     * 二分查找，在数组array中查找目标值target
     * 找相同值中的最左边一个，如果没有则返回该值的插入位置
     *
     * @param array  数组
     * @param target 需要查找的目标值
     * @return 目标值的索引位置，没有找到则返回-1
     */
    public static int leftmost(int[] array, int target) {
        int i = 0;
        int j = array.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target > array[m]) {
                i = m + 1;
            } else {
                j = m - 1;
            }
        }
        return i;
    }

    /**
     * 测试运行
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {7, 14, 28, 28, 28, 28, 35, 42, 49, 56};
        
        int i = leftmost(a, 27);
        System.out.println("27插入的位置索引是：" + i);//27插入的位置索引是：2

        int i2 = leftmost(a, 28);
        System.out.println("28最左侧的位置索引是：" + i2);//28最左侧的位置索引是：2

        int i3 = leftmost(a, 29);
        System.out.println("29插入的位置索引是：" + i3);//29插入的位置索引是：6
    }
}

这种方法可以应用到
   比如：
      求排名：某一个班级的同学成绩排名。
      求前者：某一个同学的前面排名是谁（索引减1）。
      求后者的代码不一样。改动如下（索引加1）

public class Test2 {
    /**
     * 二分查找，在数组array中查找目标值target
     * 找相同值中的最右边一个
     *
     * @param array  数组
     * @param target 需要查找的目标值
     * @return 目标值的索引位置，没有找到则返回-1
     */
    public static int rightmost(int[] array, int target) {
        int i = 0;
        int j = array.length - 1;
        while (i <= j) {
            int m = (i + j) >>> 1;
            if (target < array[m]) {
                j = m - 1;
            } else {
                i = m + 1;
            }
        }
        return j;
    }

    /**
     * 测试运行
     *
     * @param args
     */
    public static void main(String[] args) {
        int[] a = {7, 14, 28, 28, 28, 28, 35, 42, 49, 56};
        int j = rightmost(a, 28);
        System.out.println("28最右侧的位置索引是：" + j);//28最右侧的位置索引是：5
    }
}