SURF和SIFT算法

最新推荐文章于 2024-03-19 23:15:34 发布

原创最新推荐文章于 2024-03-19 23:15:34 发布 · 313 阅读

3 ·

CC 4.0 BY-SA版权

OpenCV 专栏收录该内容

21 篇文章

订阅专栏

本文深入讲解了SURF算法的关键步骤，包括积分图像、海森矩阵、尺度空间构建、特征点定位与描述。SURF通过Hessian矩阵高效检测图像特征，采用非极大值抑制和线性插值提高特征点准确性，并利用Haar小波响应统计确定主方向。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.积分图像

积分图像，就是当前的每个像素的灰度都是它与坐标原点（0,0）形成的对角线的矩形内的所有像素的灰度值之和。如下图
在这里插入图片描述
图中蓝色像素的积分图像的灰度值就是黄色框内的所有像素的灰度值之和。其他像素同样的计算方法。
有了积分图像的概念，在计算某个矩形框内的像素灰度值之和时，就可以很简单的得出了。如下图

灰色矩形框内的灰度值之和就是A+D-C-B

积分图像的作用:积分图像是SURF算法减小计算量的关键，从SIFT到SURF算法的性能提升很大程度归功于积分图像的使用，因为矩形的面积大小不会影响到运算量。任意矩形内的像素累加只需要使用矩形四个顶角位置的积分像素值进行加减运算即可得到

2.海森矩阵（Hessian matrix或Hessian）

在数学中，海森矩阵（Hessian matrix或Hessian）是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵。为了方便运算，假设函数 $f (x, y)$ ，Hessian矩阵H是函数、偏导数组成。首先来看看图像中某个像素点的Hessian矩阵，如下：

$y))=\left[ \begin{array}{ll}{\frac{\partial_{2} f}{\partial x^{2}}} & {\frac{\partial_{2} f}{\partial x \partial y}} \\ {\frac{\partial_{2} f}{\partial x \partial y}} & {\frac{\partial_{2} f}{\partial y^{2}}}\end{array}\right]$
即每一个像素点都可以求出一个Hessian矩阵。
H矩阵判别式为：
$\operatorname{det}(H)=\frac{\partial^{2} f \partial^{2} f}{\partial x^{2} \partial y^{2}}-\left(\frac{\partial^{2} f}{\partial x \partial y}\right)^{2}$
判别式的值是H矩阵的特征值，可以利用判定结果的符号将所有点分类，根据判别式取值正负，来判别该点是或不是极值点。

在SURF算法中，用图像像素 $l （ x ， y ）$ 即为函数值 $f （ x ， y ）$ ，选用二阶标准高斯函数 $g(σ)=∂2g(σ)∂x2g(\sigma)=\frac{\partial^{2} g(\sigma)}{\partial x^{2}}$ 作为滤波器，通过特定核间的卷积计算二阶偏导数，这样便能计算出H矩阵的三个矩阵元素 $L_{xx}$ 、 $L_{xy}$ 、 $L_{yy}$ ，从而计算出H矩阵：
在这里插入图片描述

为平衡准确值与近似值间的误差引入权值，权值随尺度变化，则H矩阵判别式可表示为：

$\operatorname{det}(\text {Happrox})=L x x L y y-\left(0.9 L_{x y}\right)^{2}$

其中0.9是论文作者给出的一个经验值。

为了找出图像中的特征点，需要对原图进行变换，在sift算法中，实在DOG图像中进行，在surf算法中该变换图就是原图每个像素的Hessian矩阵行列式的近似值构成，即上面的特征值。
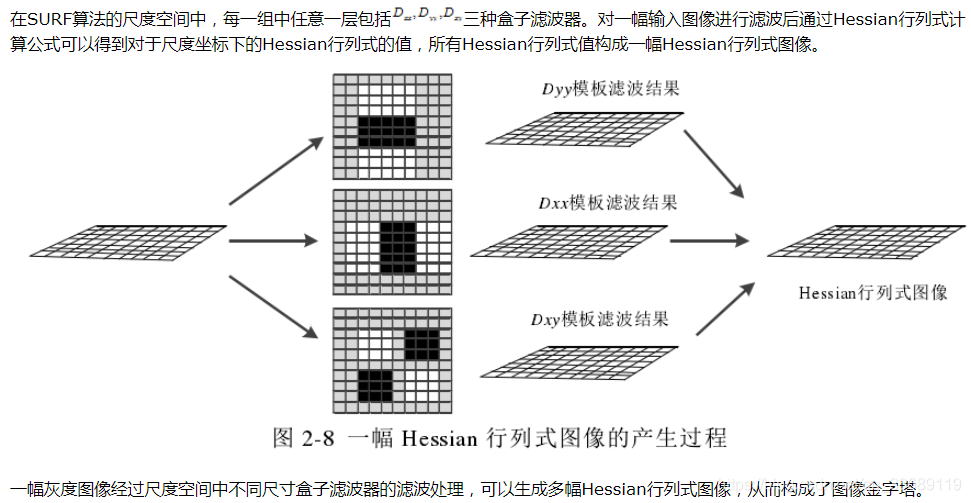
由于求Hessian时要先高斯平滑，然后求二阶导数，这在离散的像素点是用模板卷积形成的，这2种操作合在一起用一个模板代替就可以了，比如说y方向上的模板如下，以9*9的模板为例：
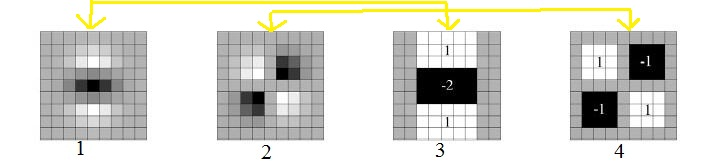
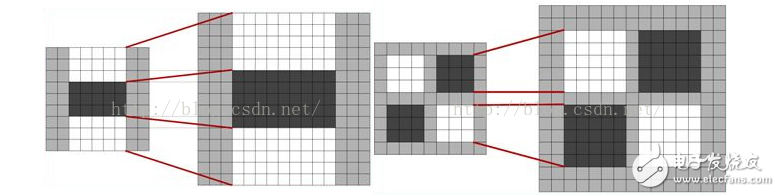
在这里插入图片描述
图中灰色像素代表0；上图中1为y方向的先高斯滤波然后二阶求导的处理，近似处理为图3，图2位x和y方向上的先高斯滤波然后二阶混合偏导，近似为图4。

网格中渐变的颜色深度代表高斯滤波模板中不同的权重系数。图3图4就是盒子滤波器
简化过程中则将权重给忽略了

有了这个近似的模板以后，计算高斯滤波和二阶导数两个步骤就可以一个步骤完成，同时，为了提高计算效率，还引入了上面的积分图像，提高了速度。

3.尺度空间

上述工作是通过模板卷积求二阶偏导数得到H矩阵，接下来要通过H矩阵构建尺度空间。

3.1 SIFT尺度空间

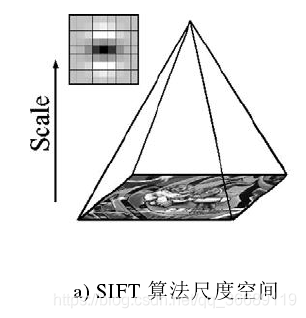
在SIFT中，尺度空间是用金字塔模型对图像滤波缩放得到的。SIFT算法首先对一幅图片进行下采样得到若干图像，每次下采样得到的图片作为每一层的原始图像。为了保证图像金字塔的连续性，对每层的原始图像以不同的进行高斯滤波，金字塔每层中又得到若干滤波后的图像。

这样得到的图像金字塔分为若干层（Octave），同时每组又有若干层（Layer）图片组成。显然，图像金字塔的计算量会随着金字塔组数和层数的增加而变大。
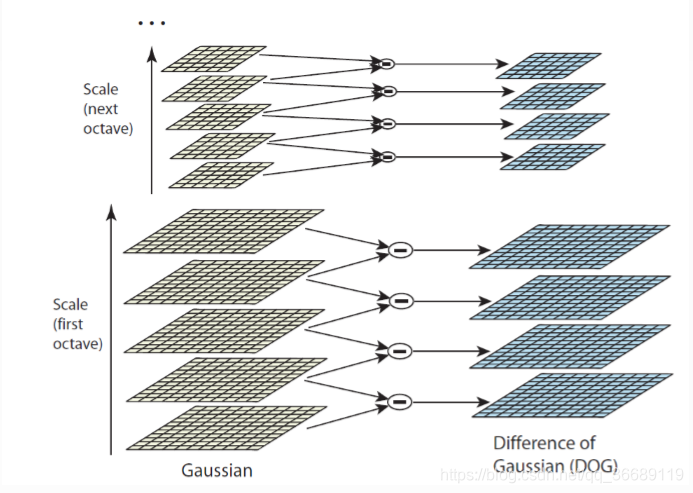
在这里插入图片描述

在这里插入图片描述

3.2 SURT尺度空间

在sift算法中，同一个octave层中的图片尺寸（即大小）相同，但是尺度（即模糊程度）不同，而不同的octave层中的图片尺寸大小也不相同，因为它是由上一层图片降采样得到的。在进行高斯模糊时，sift的高斯模板大小是始终不变的，只是在不同的octave之间改变图片的大小。而在surf中，图片的大小是一直不变的，不同octave层的待检测图片是改变高斯模糊尺寸大小得到的，当然了，同一个octave中不同图片用到的高斯模板尺度也不同。算法允许尺度空间多层图像同时被处理，不需对图像进行二次抽样，从而提高算法性能。

SURF算法中不会对图片进行下采样。SURF算法先从尺寸的盒子滤波器开始，对盒子滤波器的尺寸进行扩展，尺寸的盒子滤波器是为1.2时的高斯二阶微分函数经过离散和减裁后的滤波模板。在SURF中，我们保持图像不变，仅仅改变高斯滤波窗口的大小来获得不同尺度的图像，即构成了尺度空间。

那么接下来的每组，是通过逐渐增大的模板来进行滤波图像，一般情况下，滤波器的大小以99，1515，2121，2727等变化，随着尺度增加，滤波器大小之间的差别也在增加。
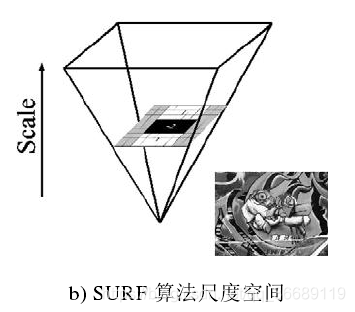
在这里插入图片描述

在这里插入图片描述

类似与SIFT中DOG金字塔，SURF用近似的Hessian行列式图作为金字塔
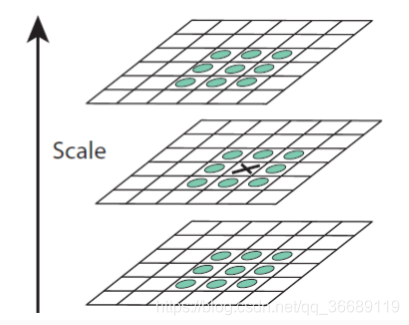
在这里插入图片描述

4.利用非极大值抑制初步确定特征点

此步骤和sift类似，将经过hessian矩阵处理过的每个像素点与其三维领域的26个点进行大小比较，如果它是这26个点中的最大值或者最小值，则保留下来，当做初步的特征点。检测过程中使用与该尺度层图像解析度相对应大小的滤波器进行检测。以3×3的滤波器为例，该尺度层图像中9个像素点之一的检测特征点与自身尺度层中其余8个点和在其之上及之下的两个尺度层的各9个点进行比较，共26个点，图11.4中标记的“x”的像素点的特征值若大于周围像素，则可确定该点为该区域的特征点。

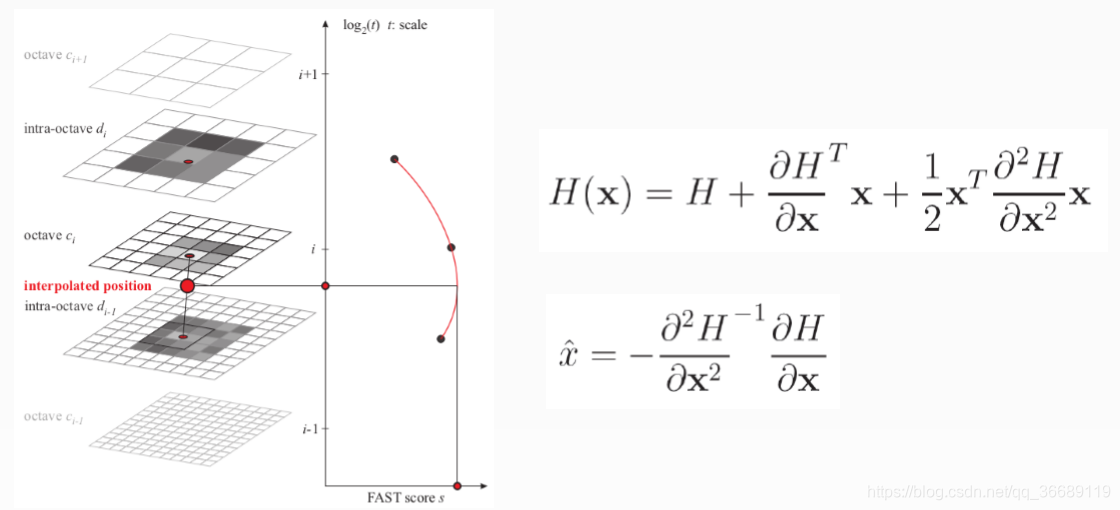
在这里插入图片描述

5.精确定位极值点

这里也和sift算法中的类似，采用三维线性插值法得到亚像素级的特征点，同时也去掉那些值小于一定阀值的点，增加极值使检测到的特征点数量减少，最终只有几个特征最强点会被检测出来。
在这里插入图片描述

6.选取特征点的主方向

6.1 SIFT

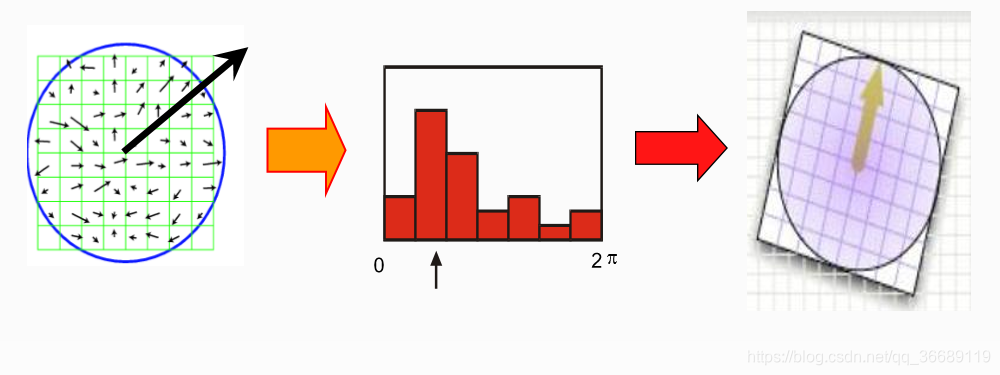
在这里插入图片描述

Sift选取特征点主方向是采用在特征点领域内统计其梯度直方图，取直方图bin值最大的以及超过最大bin值80%的那些方向做为特征点的主方向。

6.2 SURF

为了使特征具备较好的旋转不变性，需分配给每个特征点一个主方向。在SURF中，主方向是对以特征点为中心的6倍特征尺度为半径的圆形区域内的Haar小波响应做统计运算得到的。

首先赋予每一个兴趣点方向特征。我们以某个兴趣点为圆心，以6S（S为该兴趣点对应的尺度）为半径的圆形领域里，用尺寸为4S的Haar小波模板对图像进行处理，求x,y两个方向的Haar小波响应。

Haar小波的模板如图所示，

在这里插入图片描述
其中左侧模板计算X方向的响应，右侧模板计算y方向的响应，黑色表示-1，白色表示+1。用其对圆形领域进行处理后，就得到了该领域内每个点对应的x,y方向的响应，然后用以兴趣点为中心的高斯函数对这些响应进行加权

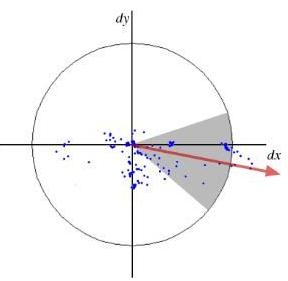
在这个圆形领域内做一个60度的扇形区域，统计这个扇形区域内的haar小波特征总和，然后转动扇形区域，再统计小波特征总和。小波特征总和最大的方向为主方向。
在这里插入图片描述

7.特征点描述算子

7.1 SIFT

在SIFT中关键点描述是选取了关键点周围 $16 x 16$ 的领域，又将其划分为 $4 x 4$ 的区域，每个区域统计8个方向梯度，最后得到 $4 x 4 x 8 = 128$ 维度的描述向量。

7.2 SURF

在SURF中，我们在关键点周围选取一个正方形框，方向为关键点的主方向，边长为20S。将其划分为16个区域（边长为5S），每个区域统计25个像素的水平方向和垂直方向的Haar小波特性（均相对于正方形框的主方向确定的）
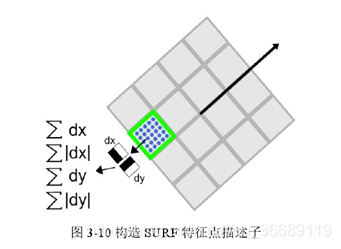
在这里插入图片描述

该小波特征包括水平方向值之和，水平方向绝对值之和，垂直方向值之和和垂直方向绝对值之和（为了把强度变化的极性信息也包括描述符中，所以对绝对值进行累加） $v=\left(\sum d_{x}, \sum d_{y}, \sum\left|d_{x}\right|, \sum\left|d_{y}\right|\right)$ 。这样每个区域有4个值，则每个正方形框有维，即每个关键点描述是64维，比SIFT描述少了一半.

8.总结

Surf采用Henssian矩阵获取图像局部最值十分稳定，但是在求主方向阶段太过于依赖局部区域像素的梯度方向，有可能使找到的主方向不准确。后面的特征向量提取以及匹配都严重依赖于主方向，即使不大偏差角度也可以造成后面特征匹配的放大误差，从而使匹配不成功。另外图像金字塔的层取得不够紧密也会使得尺度有误差，后面的特征向量提取同样依赖相应的尺度，发明者在这个问题上的折中解决方法是取适量的层然后进行插值。

在这里插入图片描述

参考博客：https://blog.youkuaiyun.com/ecnu18918079120/article/details/78195792
https://www.cnblogs.com/gfgwxw/p/9415218.html
http://www.elecfans.com/d/603768.html

https://zhuanlan.zhihu.com/c_154380889