Mean Field Multi-Agent Reinforcement Learning

这是18 ICML的文章，文中的证明推理很多，主要借鉴一下思想。

文章首先阐述了以前的一些找Nash平衡等方法对于大规模agent合作或者对抗的计算量要求很大。因此提出了这个算法。

首先介绍了Stochastic Game的环境：

第一个参数是状态空间，随后的N个参数是agent i的动作空间，在随后是agent i 的奖励函数，p是转移函数，y是折扣因子

每个agent j 根据自己的策略选择动作，其中是agent j 在动作空间上的概率分布。

表示joint policy，在这个joint policy下，agent j 的 value function可以写成：

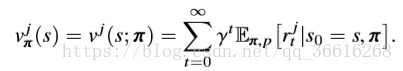
agent j 的Q function可以写成：

所以value function又可以被Q表示为

随后是Nash Q-learning

每个agent的目标学习一个最优的策略去maximize他们的value function，对于agent j 取最优的policy 取决于 joint policy。

因此在Stochastic game 中Nash 平衡被描述为：

在Nash平衡中每个agent把自己最好的respones反馈给其他的agent，因此给出了一个Nash policy 的value function

因此此时我们可以使用Nash value function重写Q function：

其中，

随后开始介绍Mean Field MARL：

首先为了解决所有的agent不能都同时策略的进行行为并同时更新标准Q function这一问题。

我们重构了Q function：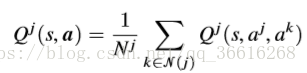

是 j 附近的agent。这里不同的N（j）要根据不同的环境，有区别的取设置

这样就有效的降低了整体的复杂度。

随后是Mean Field Approximation：（这一阶比较趋紧与证明）

我们根据1971年提出的mean field theory可以用于拟合

这里我们考虑离散的动作空间，同时我们把agent j 的aj使用one hot 编码：，随后我们根据agent j的邻居agents计算 mean action 平均动作，随后我们把每个邻居agent k的的one hot  action ak全部用 与的加和表示：

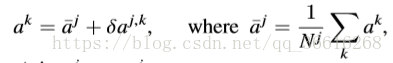
其中，可以被解释为agent j的附近agents动作的经验分布。

随后是对Qj的推到：

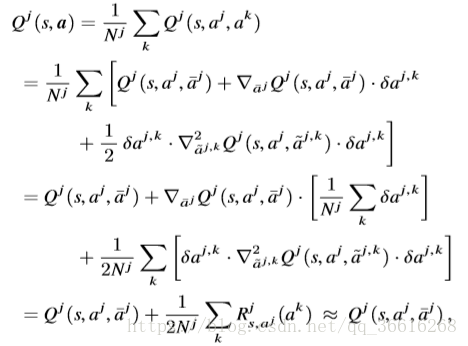
最后的结论很重要也就是最后近似等于。

我们可以看下面这个图来近似：

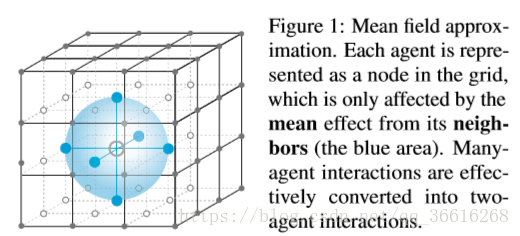
此时Q函数的更新函数可以写为：

此时agent j的mean field 的value function 可以写成：

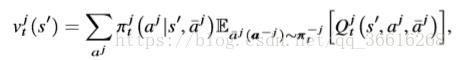
接着我们给出了计算每个agent j 的最好策略的迭代过程，其中mean action ：

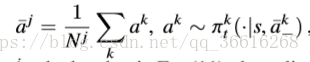，eq（11） 随后policy 根据mean action更改：

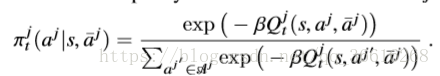eq（12）

为了区分与Nash平衡，我们标记mean field，Q function：

。随后开始证明mean field会像Nash 平衡一样收敛

MFQ:

loss function :

也就是说yj是Q target计算出来的，是Q est计算出来的

伪代码：

MFAC:

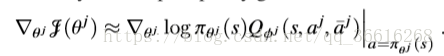
他的所有实验都是共享网络的，也就是一个Target Net 一个Est Net，然后每个agent之间唯一的不同点就是mean action的影响，不然只要这个agent在这个位置，那么他就会做出确定的动作，而不会考取其他agent的动作。