KMP算法

概述

问题：

在字符串（也叫主串）中的模式（pattern）定位问题。说简单点就是我们平时常说的关键字搜索。模式串就是关键字（接下来称它为P），如果它在一个主串（接下来称为T）中出现，就返回它的具体位置，否则返回-1（常用手段）。

Brute-Force

要在T中找到P，暴力法的做法是从左到右一个个匹配，在T中用 i 标记，P中用 j 标记，依次比较 i+1 , j+1、i+2 , j+2 ……
当 i+3 , j+3 不同时，暴力法将 i 退回 i+1 ，重置 j ，直到完全相等。

/**
 * 暴力破解法
 * @param ts 主串
 * @param ps 模式串
 * @return 如果找到，返回在主串中第一个字符出现的下标，否则为-1
 */
int bf(String ts, String ps) {
    char[] t = ts.toCharArray();
    char[] p = ps.toCharArray();
    int i = 0; // 主串的位置
    int j = 0; // 模式串的位置
    while (i < t.length && j < p.length) {
       if (t[i] == p[j]) { // 当两个字符相同，就比较下一个
           i++;
           j++;
       } else {
           i = i - j + 1; // 一旦不匹配，i后退
           j = 0; // j归0
       }
    }
    if (j == p.length) {
       return i - j;
    } 
    else {
       return -1;
    }
}

在 Brute-Force 中，如果从 T[i] 开始的那一趟比较失败了，算法会直接开始尝试从 T[i+1] 开始比较。这种行为，属于典型的“没有从之前的错误中学到东西”。我们应当注意到，一次失败的匹配，会给我们提供宝贵的信息:

如果 T[i : i+len§] 与 P 的匹配是在第 r 个位置失败的，那么从 T[i] 开始的 (r-1) 个连续字符，一定与 P 的前 (r-1) 个字符一模一样

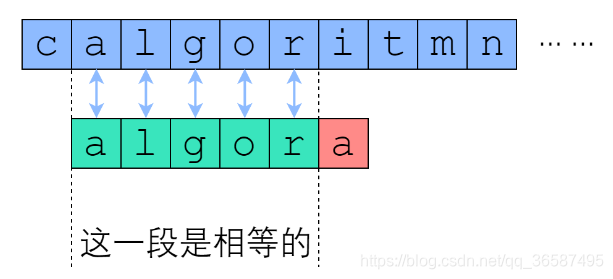
优化 Brute-Force 的路线是“尽量减少比较的趟数”，而如果我们跳过那些绝不可能成功的字符串比较，则可以希望复杂度降低到能接受的范围。

接下来来减少绝对不可能成功的情况：

首先，利用上一节的结论。既然是在 P[5] 失配的，那么说明 T[0:5] 等于 P[0:5]，即"abcab". 现在我们来考虑：从 T[1]、T[2]、T[3] 、T[4]、T[5]开始的匹配尝试，有没有可能成功？　　从 T[1] 开始肯定没办法成功，因为 T[1] = P[1] = ‘b’，和 P[0] 并不相等。从 T[2] 开始也是没戏的，因为 T[2] = P[2] = ‘c’，并不等于P[0]. 但是从 T[3] 开始是有可能成功的,T[3] = P[3] = ‘a’。至少按照已知的信息，是有可能成功的。

为了保留这个相同的字符信息，我们引入next数组：

next数组是对于模式串而言的。P 的 next 数组定义为：next[i] 表示 P[0] ~ P[i] 这一个子串，使得 前k个字符恰等于后k个字符 的最大的k. 特别地，k不能取i+1（因为这个子串一共才 i+1 个字符，自己肯定与自己相等，就没有意义了）。

i=0 a 0
i=1 ab 0
i=2 abc 0
i=3 abca a=a， 1
i=4 abcab ab=ab ，2
i=5 abcabd 0

第一次改进

Brute-Force 就是每次失配之后只右移一位；改进算法则是每次失配之后，移很多位，跳过那些不可能匹配成功的位置。但是该如何确定要移多少位呢？

因此我们在模式串的j位失败后，在主串 j - next[j - 1] 位开始重新匹配

当i=0时，在模式串第3位匹配失败，因此下一次主串i位置在0+3-next[2]=2
当i=2时，在模式串第6位匹配失败，因此下一次主串i位置在2+6-next[5]=3
依此类推，直到 j = P.len - 1

根据 next数组的性质：P[0] 到 P[r] 这一段子串中，前next[r]个字符与后next[r]个字符一模一样。既然如此，如果失配在 P[j], 那么在这j-1个字符中，前next[j-1]与后next[j-1]个字符是一样的，在主串中，这next[j-1]已经有了，因此我们可以很明确主串的这j-1个字符中的后next[j-1]个字符是能匹配的

因此主串的 i 直接可以从 i 变为 i + j - next[j - 1]

int KMP(String s,String t)
{
   int next[MaxSize],i=0;j=0;
   Getnext(t,next);
   while(i<s.length&&j<t.length)
   {
      if(j==-1 || s[i]==t[j])
      {
         i++;
         j++;
      }
      else j=next[j];               //j回退。。。
   }
   if(j>=t.length)
       return (i-t.length);         //匹配成功，返回子串的位置
   else
      return (-1);                  //没找到
}

快速求next数组

首先我们知道 next[0] = 0，当j ≥ 1时，如果我们已知了next[j - 1]，那么next[j]怎么求得呢？
假定我们给定了某模式串，且已知next[j - 1] = k，现在求得next[j]等于多少。

1.当pk=pj时，有 next[j] = next[j - 1] + 1 = k + 1

2.当pk≠pj时，有p0p1…pk-1pk != pj-kpj-k+1…pj-1pj，此时 我们需要递归的在前j-1个字符中进行上述判别。

int GetNext(int j,char T[])
{
	if(j==0)return -1;
	if(j>0)
	{
		int k=GetNext(j-1,T);
		while(k>=0)
		{
			if(T[j-1]==T[k])return k+1;
			else k=GetNext(k,T);
		}
		return 0;
	}
	return 0;
}