使用内点法解决线性规划问题

qq_36573282

于 2020-05-15 08:25:51 发布

阅读量1.7k

点赞数

文章标签：凸优化内点法线性规划

本文链接：https://blog.youkuaiyun.com/qq_36573282/article/details/106133725

版权

本文详细介绍了如何使用内点法解决线性规划问题。通过一个简单的线性规划例子，阐述了问题描述、建模过程，并利用拉格朗日乘子法转化为包含对数函数的优化目标。通过求导分析，展示了内点法的迭代过程，指出在实际运行中从点(3,3)开始能收敛到接近最优解(1.58,1.58)。最后提到了代码实现并提供了Github链接。" 107225006,7977928,Windows10上安装MongoDB 4.2.8步骤,"['数据库', 'MongoDB', 'Windows安装', '服务配置']

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

使用内点法解决线性规划问题

1. 问题描述

这里以一个简单的线性函数为例子：
$\min\ \ x+y\\ s.t.\ \ x+2y \leq 10\\ \ \ \ \ 2x+y\leq 10\\ \ \ \ \ x \geq 0\\ \ \ \ \ y \geq 0$
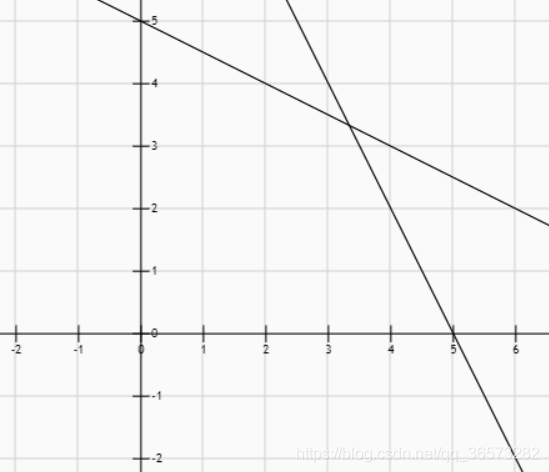
最终，可行域在下图中中间那部分，结合图像可以很容易的得到最优值为0。但是如何要使用程序从可行域的某个起始点收敛到最优值。
在这里插入图片描述

2. 问题建模

线性规划问题的一般形式为：

$\min\ \ c^T X\\ s.t.\ \ AX \leq b$
因此，对上一部分的那个例子按照这种形式表示，设 $c=\left(\begin{matrix} 1\\ 1 \end{matrix}\right), A=\left(\begin{matrix} 1 & 2\\ 2 & 1\\ -1 & 0\\ 0 & -1 \end{matrix}\right),b=\left(\begin{matrix} 1\\ 1\\ 0\\ 0 \end{matrix}\right),X=\left(\begin{matrix} x\\ y \end{matrix}\right)$

最低0.47元/天解锁文章