数据结构与算法(十七)选择排序

选择排序(Selection Sort)就是遍历n-1次数组，每次从待排序的数据中找出一个最小值或最大值，与第i位置上的数据进行交换。

首先我们需要一个待排序的数组 arr[10] = {0, 9, 1, 5, 8, 3, 7, 4, 6, 2}，其中arr[0]=0用做哨兵或临时变量所以不参与排序，所以数组下标从1开始，有效长度len=9，实际长度为10。

然后我们还需要交换数据的操作：

void swap_arr(int *arr, int i, int j)
{
    int temp = arr[i];
    arr[i]   = arr[j];
    arr[j]   = temp;
}

 1、选择排序

/*选择排序算法*/
void Selection_Sort(int *arr, int len)
{
    int min;                            /*记录每一次循环的最小值*/
    for (int i=1;i<len;i++)             /*需要循环len-1次*/
    {
        min=i;                          
        for (int j=i+1;j<=len;j++)  
        {
            if (arr[min]>arr[j]) min=j; /*min移动到更小值的位置*/
        } 
        if (min!=i)                     /*如果i刚好就是最小值，那就不用交换*/
            swap_arr(arr, i, min);      /*否则就交换到i位置*/
    }
}

其实选择排序的思路非常的好理解，代码实现也非常简单，下面给出前三轮循环的交换示意图。 

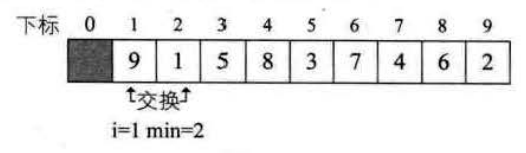
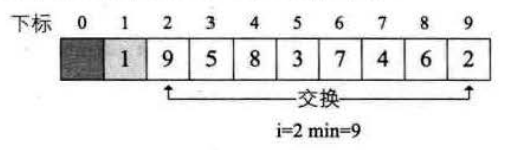
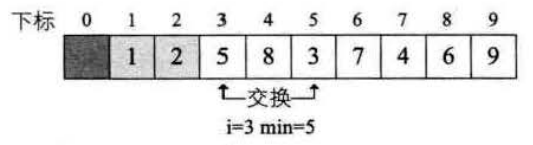
通过分析选择排序，知道它是一个萝卜一个坑的填法，是不区分最好情况和最坏情况的，内层循环次数还会逐轮递减，所以选择排序的时间复杂度O(n²/2)。

在所有情况下，选择排序的效率都优于标准冒泡排序，性能是其的一倍，而优化后的冒泡排序仅在较好的情况下略优于选择排序。

2、优化选择排序

又要问了，标准的选择排序是否还有优化的空间吗？

因为选择排序不区分最好情况和最坏情况，也无法每轮辨别是否已经完全排序好了，所以之前优化冒泡排序的思路用不了。

但是想一想，一次遍历只找一个最小值，是不是有些亏？我们还可以再找一个最大值，这样一轮就可以排序一个最大值和一个最小值，这个思路有点像鸡尾酒排序对于冒泡排序的优化思路。

/*选择排序优化算法*/
void Optimal_Selection_Sort(int *arr, int len)
{
    int min, max;                        /*记录每一次循环的最小值和最大值*/
    for (int i=1;i<=len/2;i++)           /*因为一轮可以排序两个数据，所以轮数减半*/
    {
        min=max=i;    
        for (int j=i+1;j<=len-i+1;j++)   /*每轮j的前后范围都会减少一个*/
        {
            if (arr[min]>arr[j]) min=j;
            if (arr[max]<arr[j]) max=j;
        } 
        if (min!=i) {                    /*如果i刚好就是最小值，那就不用交换*/
            if (max == i)                /*但是如果刚好最大值在最小值要去的位置*/
                max=min;                 /*交换后，最大值到了原本最小值的位置*/
            swap_arr(arr, i, min);
        }
        if (max!=len-i+1)                /*如果刚好就是最大值，那就不用交换*/
            swap_arr(arr, len-i+1, max);
    }
}

优化后的选择排序，原来外层循环次数减少了一半，因此排序效率提升了一倍，所以优化后的选择排序的时间复杂度变为O(n²/4)，但仍是平方阶的时间复杂度，没有质变。

优化后的选择排序在较好情况下的性能也要略优或持平于优化后的冒泡排序了。

3、链表实现优化选择排序

/*链表实现选择排序优化算法*/
void Optimal_Selection_Sort_LinkList(LinkList Head)
{
    LinkList min, max;                          /*min和max指针指向最大值和最小值的结点*/
    LinkList End = NULL;                        /*End指针指向已经排好序的结点们的最前面结点，与(len-i+1)作用一样*/
	                                            /*一开始End为NULL，说明End在序列外，序列还未排序*/
    LinkList p, q;                           
    for (p=Head->next;p->next!=End;p=p->next)   /*因为是链表，无法根据下标使轮数减半*/
    {                                           /*因此需要根据End指针来判断后面都有序了，使轮数减半*/
        min=max=p;                              /*min和max指针指向未排序的第一个结点p*/
        for (q=p->next;q->next!=End;q=q->next)  /*q从p的下一个结点开始，然后停在End前一个结点*/
        {
            if (min->data > q->data) min=q;
            if (max->data < q->data) max=q;
        }
        if (min->data > q->data) min=q;         /*q->next==End时会跳出，此时q就没进行比较，所以多加一次比较*/
        if (max->data < q->data) max=q;         /*也可以使用while循环来优化这一段代码*/
        End=q;                                  /*End前移，等待这一轮最大值交换到此处*/
        if (min!=p) {                           /*最小值交换到p*/
            if (max==p) max=min;
            swap_link(min,p);
        }
        if (max!=End)                           /*最大值交换到End*/
            swap_link(max,End);
        if (End == p->next) break;     /*为什么会多出这一句？因为会出现：当这一轮p后移的时候，此时End还不等于p->next*/
    }                                  /*这一轮结束后，此时End可能会等于p->next，但是下一轮p是先后移再判断*/
}                                      /*此时p就会等于End，p->next!=End永远不会跳出循环，所以要加这一句*/

链式存储结构实现优化选择排序，如果不使用length来实现，那么需要增加一个End指针来替代len-i+1的作用，其他实现思路与顺序存储结构实现优化选择排序一模一样，性能和效率也是一样的。