排序算法小结

学习自https://www.cnblogs.com/wxisme/p/5243631.html

 

冒泡

怎么浮动一个元素的？

void fuction(int a[]) {
    for(int size = a.length, i = 0; i < size - 1; i ++) {
        int val = a[i];
        int val2 = a[i + 1];
        if(val > val2) {
            a[i] = val2;
            a[i + 1] = val;
        }
    }
}

接下来一次需要size-2了！所以我们用一个循环来控制这个值。

void fuction(int a[]) {
    for(int size = a.length, j = size - 1; j >= 1; j --) {
        for(int i = 0; i < j; i ++) {
            int val = a[i];
            int val2 = a[i + 1];
            if(val > val2) {
                a[i] = val2;
                a[i + 1] = val;
            }
        }
    }
}

冒泡总而言之就是找到最大的元素，然后一格格移动到最右端。n^2 

冒泡还有逆序已有序的优化。

 

选择排序

找到最大的元素，直接移动到应该移动到的位置，而不是一格格的移动

void function(int a[]) {
    int max = a[0];
    int index = 0;
    for(int size = a.length, i = 0; i < size - 1; i ++) {
        int val = a[i];
        if(a[i] > max) {
            max = a[i];
            index = i;
        }
    }
    int last = a[a.length - 1];
    if(max > last) {
        a[a.length - 1] = max;
        a[index] = last;
    }
}

像冒泡一样，写出一个循环就可以，所以后面的就不写了

 

插入排序

第一个数肯定是已经有序了，看成一个有序整体。再看第二个数就不一定了，所以需要选择一个合适的位置插入进去，再次有序。

void function(int a[], int index) {
    //index之前的已经全部有序了，然后我们需要从后往前遍历，找到比a[index]小的数，然后插入到这个数的前面
    int waitingInsertValue = a[index];
    for(int i = index - 2; i >= 0; i ++) {
        int val = a[i];
        if(val < waitingInsertValue) {
            //插入到这之前，并移动数组上的元素
            break;
        }
        if(i == 0) {
            //没找到，那就放在第一个
        }
    }
}

 

快速排序

void function(int a[]) {
    int n = a.length;

    int  val = a[0];

    int left = 1;
    int right = n - 1;

    while(left < right) {

        while(left < right) {
            //从右边开始找，找一个比坑小的数
            int currentVal = a[right];
            if(currentVal < val) {
                a[left] = currentVal;
                break;
            }
        }

        //同理
    }

    //最后把原来的数放进去
    //继续递归
}

快排就是确定第一个数， 并且提取出来，然后从右边找到比这个数小的，从左边找到比这个数大的，两边同时递归到中间， 确保了左边都是比他小的，右边都是比他大的，最后再把原来的数放进去就可以了（说实话，流传的挖坑填埋法不太容易真正理清快排的思路）

 

堆排序
这样用数组表示堆

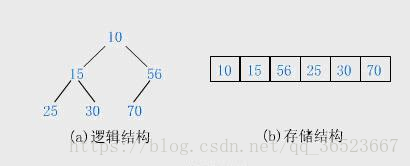
假设一个堆

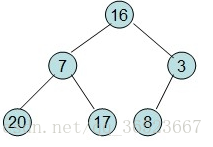
从8、17、20...一个个开始调整

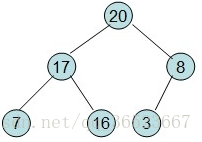
这样最大树就浮到顶端了，然后20和3交换

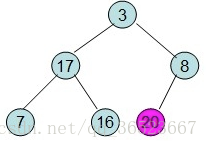
20就已经有序了，接下来重新维持平衡，以此类推

void function(int a[]) {

    //从根节点怎么对应到左右子节点？2*i+1 2*i+2
    //从子节点怎么对应到根节点？i/2向上取整-1
    //简单推推公式就可以推出来

    //然后交换还没就绪的最后一个数
    for (int i = a.length - 1; i >= 1; i --) {
        //构造初始堆
        init(a, i);
        //交换数组的0,i...
    }
}

void init(int a[], int lastIndex) {
    //逆序遍历，第一个不用遍历了
    for (int i = lastIndex; i >= 1; i --) {
        int val = a[i];
        int parent;
        if (i % 2 != 0) {
            parent = a[(i - 1) / 2];
        } else {
            parent = a[(i - 2) / 2];
        }
        if(val > parent) {
            //交换...
        }
    }
}

 

希尔排序

图来自https://blog.youkuaiyun.com/morewindows/article/details/6668714

void function(int a[]) {
    int n = a.length;

    while(n != 0) {
        n = n / 2;

        //所以0,1,...,n-1，各自加上n * x就是自己的队伍了
        for (int i = 0; i < n; i ++) {
            for (int j = i + n; j < n; j += n) {
                //从i+n开始，因为第一个单独一个已经有序
                //如果当前数小于上一个数
                if (a[j] < a[j - 5]) {
                    //找到自己该在的位置并插入...
                }
            }
        }
    }
}

 

归并排序

底层划分为1个单元，然后彼此合并。但是直接开循环写很麻烦，所以需要通过递归

void function(int a[], int start, int end) {
    if (start < end) {//这样判断，使得底层的单元为1，这个时候递归就终止了，然后合并，向上返回
        int mid = (start + end) / 2;

        //左边递归下去，直到只剩下一个数，递归结束，合并两个数，然后向上返回，最后左边全部有序了
        function(a, start, mid);
        //右边递归
        function(a, mid + 1, end);

        //合并两者 从start-mid,mid+1-end。需要借助一个临时数组，最后拷贝到原数组里去...
    }
}

 

计数排序

详细思路可以看https://blog.youkuaiyun.com/u012918361/article/details/70185637

网上的思路：首先获取最大值与最小值的差值+1，再以此长度建立一个计数数组。然后统计这个数组中的每个数的出现次数。然后如何确定每个数的位置呢？比如一个数，对应到这个计数数组里有5个，而在这之前有x个数，所以需要右推对应的位数即可。其实可以优化一下，当你得到计数数组后，直接输出即可。

void function(int a[]) {
    int n = a.length;

    int min = a[0];
    int max = a[0];

    for (int i = 1; i < n; i ++) {
        int val = a[i];

        if(val < min) {
            min = val;
        }

        if (val > max) {
            max = val;
        }
    }

    int length = max - min + 1;

    int countRecord[] = new int[length];

    int index = 0;
    for (int i = min; i <= max; i ++) {
        int count = countRecord[i];
        if(count != 0) {
            for (int j = 0; j < count; j ++) {
                a[j] = i;
                index ++;
            }
        }
    }
}

实际两个数组就够了。

 

桶排序

我晕 感觉就是计数排序啊！

其实上面对计数排序的解释中，原有思路是计数排序，我优化后的思路是桶排序。歪打正着了。。。

 

基数排序

图来自https://blog.youkuaiyun.com/CJF_iceKing/article/details/7943609

具体代码就是先按照个位分配，把数组扔进这10个数组中，会返回一个个位从小到大的新顺序

然后按十位分配，把数组扔进这10个数组中，会返回一个从个位、十位从小到大的新顺序。。。

当然每个数组的第0位要记录一下index。

void function(int a[]) {
    int n = a.length;

    int[][] b = new int[10][n];

    for (int j = 0; j < 31; j ++) {
        for (int i = 0; i < n; i ++) {
            int val = a[i];
            int positionValue = getPositionValue(val, j);
            b[positionValue][0] ++;
            b[positionValue][b[positionValue][0]] = val;
        }
        
        //收集回原数组并清除数据
    }
}

int getPositionValue(int a, int position) {
    //返回对应位上的值，position为1代表个位，2代表十位，以此类推。值从0-9...没有这一位，那么也是0
}

其实代码可以优化，不用遍历到31位的