在不同形式傅里叶变换形式下，Fourier变换对的形式调整方法_傅里叶分解的形式可以改吗-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_36513097/article/details/104181140

探讨了在大涡模拟中，使用不同卷积核进行滤波对各向同性湍流三维能谱的影响，重点分析了盒子滤波在谱空间的应用及与Matlab FFT变换的适配问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

我在做大涡模拟（LES）的时候，需要绘制各向同性湍流的三维能谱，并且对高波数的成分进行滤波。

就在我比较采用不同形式的卷积核进行滤波，对能谱的影响的时候，我正想把盒子滤波（heaviside函数）的Fourier转化后的形式运用到谱空间。但是我发现，sagaut中的公式是不可以直接拿来用的，需要对卷积核的宽度进行一些修正，我不断调整核宽度的大小，然后与标准答案对比了一下，发现系数正好相差一个 $2\pi/N$ ,于是我就有了以下思考，并进行了验证。

总的来说，就是归因于Fourier变换的形式不统一，即matlab的fft变换的形式与sagaut的连续傅里叶变换形式的不统一。

两种Fourier变换

一本参考书中的Fourier变换

Pope在《turbulent flow》的Appendix D中，对Fourier变换的定义如下：

$g(\omega)=\mathcal{F}_p \{f(t)\}=\frac{1}{2 \pi} \int_{-\infty}^{\infty}f(t) e^{-j \omega t}dt,$

其逆变换如下：

$f(t)=\mathcal{F}_p^{-1}\{g(\omega)\}=\int_{-\infty}^{\infty}g(w)e^{j\omega t} d \omega.$

采用以上Fourier变换的定义时，Heaviside函数的Fourier变换如下：

$\mathcal{F}p\{ H(b-\mid t\mid)\}=\frac{\text{sin}(b \omega)}{\pi \omega}.$

某语言的FFT帮助函数中定义的离散傅里叶变换

而matlab 中fft(X)函数关于Fourier变换及其逆变换的定义如下：

$g(k)=\mathcal{F}_M\{f(n)\}=\sum_{n=1}^N f(n) e^{-j2\pi k n/N},k \in [1,N],$

$f(n)=\mathcal{F}^{-1}_M\{g(k)\}=\frac{1}{N} \sum_{k=1}^N g(k)e^{j2\pi k n/N}, n \in [1,N].$

有两点需要注意的是

为了比较的方便，我把指数上的(k-1)*(n-1)替换成了kn,仅仅是为了这个问题的讨论方便。
为了方便区分，我在前一种定义下采用自变量 $\omega$ 与 $t$ ，Fourier变换采用 $\mathcal{F}_p$ 表示，后一种定义采用自变量 $k$ 与自变量 $n$ ,Fourier变换采用 $\mathcal{F}_M$ 表示。

如何将前者定义下的Fourier变换对应用到matlab中？

现在需要讨论的就是如何进行 $\omega,t$ to $ k,n$ 的变换，即在调用matlab的函数的时候k与n是如何对应的。

从指数函数的指数来看，两者的指数是肯定相同的，如果假设

${\color{Red} t=n, n\in [1,N]}$

的话，很明显有

${\color{Red} \omega =2 \pi k/N, k \in [1,N]}$ ，

因此本文章的主要结论就讲完了，突然觉得有点简单。恩，下面是一些补充。

那么在matlab函数中，heviside函数的Fourier变换的形式是怎样的？

下面这个就是推导。

${\color{Red} \mathcal{F}_M\{H(b-\mid n\mid)\} =\sum_{n=1}^N f(n) e^{-j2\pi k n/N}=2\pi (\frac{1}{2\pi}\sum_{n=1}^N f(n) e^{-j(2\pi k/N) n})\\ =2 \pi \mathcal{F}p\{ H(b-\mid n\mid)\} =2 \pi \frac{\text{sin}(k \omega)}{\pi \omega}=\frac{\text{sin}( 2 \pi bk/N)}{ \pi k/N}, where \; k,n \in [1,N]. }$

红色为主要结论。

注意：本文章不讨论连续Fourier变换与离散Fourier变换之间的关系，我默认两者是近似相等的，即积分号可以变成求和。

一个用于验证的一维Fourier变换算例

在这个算例中，我采用matlab自带的fft函数对b=5的heaviside函数进行Fourier变换，然后将其高波数成分重叠到低波数成分（因为奈奎斯特采样与奈奎斯特频率）。

关于实数函数的Fourier分解的系数的模

由于变换之后是一个复数向量，但是连续Fourier变换的理论分析结果是一个实数函数，我猜测这是因为离散Fourier函数忽略了高波数成分。

于是我就想将复数向量的模与连续Fourier变换的结果系数的模进行比较。

关于模，有以下推导及定义。

假设有一个函数 $u(t)$ ,它可以Fourier分解，分解成不同的频率，每个频率的系数为 $c_k$ ，其分解如下：

$u(t)= \sum_{k=-\infty}^\infty (a_k+j b_k)e^{j \omega_k t}= \sum_{k=-\infty}^\infty c_k e^{j \omega_k t}.$

由于我们不关心相位，平均值之类的东西，所以我们可以简单的取其平均值为0，即 $c_0=0$ 。

将其余成分按照sin与cos进行拆分组合如下：

$u(t) &= \sum_{k=1}^\infty[(a_k+a_{-k})+j(b_k+b_{-k})]\text{cos}(\omega_k t)\\ &+\sum_{k=1}^\infty[j(a_k-a_{-k})+(b_k-b_{-k})]\text{sin}(\omega_k t)$

我们只讨论 $u(t)$ 是一个实数的情况，于是上式的虚部为0，所以它的系数是共轭的，即 $a_n=a_{-n},b_n=-b_{-n}$ 。

于是通过简单的变换，我们就可以进行以下简化，

$u(t) &= 2\sum_{k=1}^\infty [a_k\text{cos}(\omega_k t)-b_{k}\text{sin}(\omega_k t)]\\ &=2\sum_{k=1}^\infty \mid c_k \mid \text{cos}(\omega_k t+ \theta_k)$

其中， $\mid c_k \mid =(a_k^2+b_k^2)^{1/2}$ 是 $c_k$ 的模。

通过这一段的分析，我想要说明，Fourier变换之后的函数的模与其波数仍然是具有一一对应的关系，不会因为取模之后，某一个波数的对应值就会对其他的波数造成影响。因此，通过比较模来比较两种Fourier变换定义下的变换结果是有意义的。

计算结果

因为连续Fourier变换只有实数成分，所以只需要取其绝对值就好，但是又因为fft的结果高于奈奎斯特采样频率的部分被重叠到了低波数成分，所以连续Fourier变换的结果取绝对值之后还要乘以2。与此章的上一节分析有异曲同工之妙。

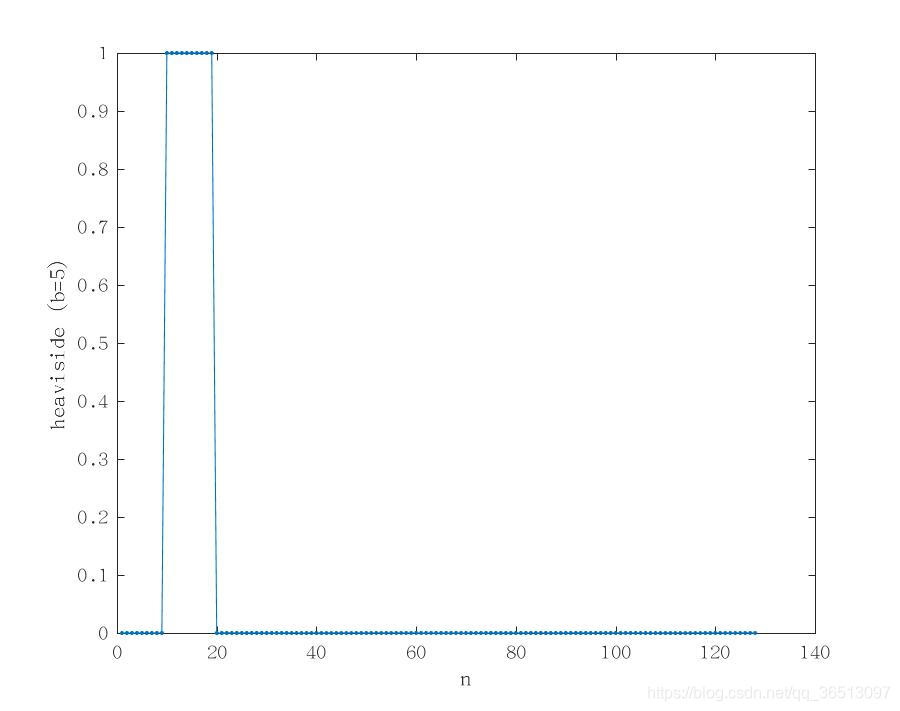
现实空间的heaviside函数的图像如下所示。

谱空间的模关于波数的函数如下所示。

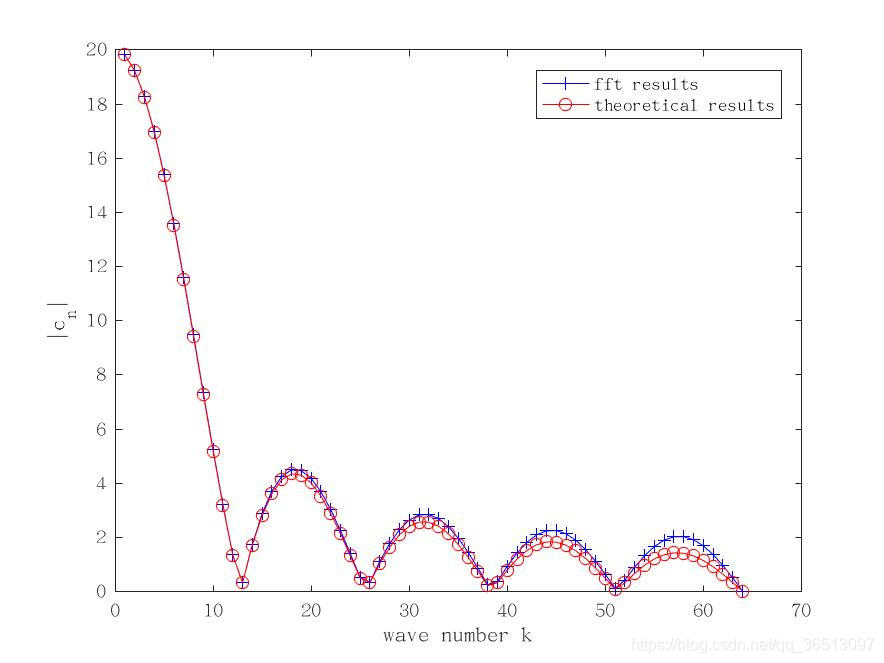
从图中可以看出，两者结果是很相近的，唯一的区别是，在较高的波数时，fft结果模偏大，猜测这可能是因为fft只能对有限波数进行计算，并不能在无限域中进行Fourier变换，所以更高波数的影响被累积到这些波数中。

两者进行比较的代码如下：

clc;clear;close all;
N=128;
n=1:N;
b=5;
%生成heaviside函数
data=(n<=(10+2*b-1)) & (n>=(10));
data_fft=fft(data);
figure;plot(data,'.-')
xlabel('n')
ylabel(strcat('heaviside (b=',num2str(b),')'))
saveas(gcf,'test_real.eps')
%fft变换后的波数折叠
data_fft=[2*data_fft(2:(N/2)) data_fft(N/2+1)];
%求fft的模
data_mod=sqrt(data_fft.*conj(data_fft));
figure;plot(data_mod,'b+-')

k=1:(N/2);
% b=5;
y=sin(2*pi*b*k/N)./(pi*k/N);
%求模与折叠
y=2*abs(y);
hold on;plot(k,y,'ro-')
xlabel('wave number k')
ylabel('|c_n|')
legend('fft results','theoretical results')
saveas(gcf,'test_fourier.eps')