图论并查集（Union-Find）算法及应用详解 & 经典算法题之朋友圈

已于 2022-04-22 16:07:47 修改
阅读量1.3k 收藏 7
点赞数 1
分类专栏： 刷题笔记 文章标签： 图搜索算法
于 2022-04-01 19:37:25 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_36389060/article/details/123890233
版权

1 并查集（Union-Find）

什么是并查集？

Union-Find 算法，也就是常说的并查集算法，主要是解决图论中 「动态连通性」 问题。

什么是动态连通性？

简单说，动态连通性其实可以抽象成给⼀幅图连线。⽐如下⾯这幅图，总共有 10 个节点，他们互不相连，分别⽤ 0~9 标记：
在这里插入图片描述
现在我们的 Union-Find 算法主要需要实现这两个 API：

class UF {
    /* 将 p 和 q 连接 */
    public void union(int p, int q);
    /* 判断 p 和 q 是否连通 */
    public boolean connected(int p, int q);
    /* 返回图中有多少个连通分量 */
    public int count();
}

这⾥所说的「连通」是⼀种等价关系，也就是说具有如下三个性质：

  • ⾃反性：节点 p 和 p 是连通的。
  • 对称性：如果节点 p 和 q 连通，那么 q 和 p 也连通。
  • 传递性：如果节点 p 和 q 连通，q 和 r 连通，那么 p 和 r 也连通。

⽐如说之前那幅图，0～9 任意两个不同的点都不连通，调⽤ connected 都会返回 false，连通分量为 10 个。

如果现在调⽤ union(0, 1) ，那么 0 和 1 被连通，连通分量降为 9 个。

再调⽤ union(1, 2)，这时 0,1,2 都被连通，调⽤ connected(0, 2) 也会返回 true，连通分量变为 8 个。
在这里插入图片描述
判断这种「等价关系」⾮常实⽤，⽐如说 编译器判断同⼀个变量的不同引⽤，⽐如 社交⽹络中的朋友圈计算 等等。

Union-Find 算法的 关键就在于 union 和 connected 函数的效率 。那么⽤什么模型来表示这幅图的连通状态呢？⽤什么数据结构来实现代码呢？

基本实现思路

我们使⽤森林（若⼲棵树）来表示图的动态连通性，⽤数组来具体实现这个森林。

怎么⽤森林来表示连通性呢？我们设定树的每个节点有⼀个指针指向其⽗节点，如果是根节点的话，这个指针指向⾃⼰。⽐如说刚才那幅 10 个节点的图，⼀开始的时候没有相互连通，就是这样：
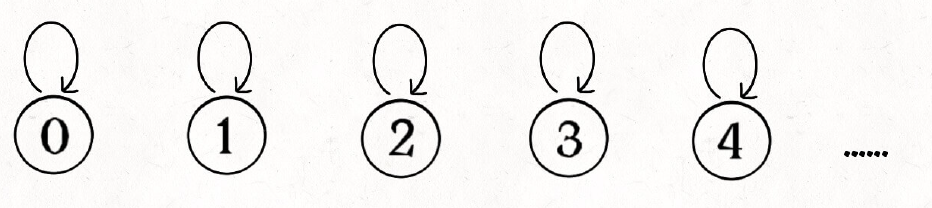
在这里插入图片描述

class UF {
    // 记录连通分量
    private int count;
    // 节点 x 的节点是 parent[x]
    private int[] parent;
    /* 构造函数，n 为图的节点总数 */
    public UF(int n) {
        // ⼀开始互不连通
        this.count = n;
        // ⽗节点指针初始指向⾃⼰
        parent = new int[n];
        for (int i = 0; i < n; i++)
            parent[i] = i;
    }
    /* 其他函数 */
}

如果某两个节点被连通，则让其中的（任意）⼀个节点的根节点接到另⼀个节点的根节点上：

在这里插入图片描述

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 将两棵树合并为⼀棵
    parent[rootP] = rootQ;
    // parent[rootQ] = rootP 也⼀样
    count--; // 两个分量合⼆为⼀
}
/* 返回某个节点 x 的根节点 */
private int find(int x) {
    // 根节点的 parent[x] == x
    while (parent[x] != x)
        x = parent[x];
    return x;
}
/* 返回当前的连通分量个数 */
public int count() {
    return count;
}

这样，如果节点 p 和 q 连通的话，它们⼀定拥有相同的根节点：
在这里插入图片描述

public boolean connected(int p, int q) {
	int rootP = find(p);
	int rootQ = find(q);
	return rootP == rootQ;
}

⾄此，Union-Find 算法就基本完成了。是不是很神奇？竟然可以这样使⽤数组来模拟出⼀个森林，如此巧妙的解决这个⽐较复杂的问题！

时间复杂度分析

那么这个算法的复杂度是多少呢？我们发现，主要 API connected 和 union 中的复杂度都是 find 函数 造成的，所以说它们的复杂度和 find ⼀样。

find 主要功能就是从某个节点向上遍历到树根，其 时间复杂度就是树的⾼度。我们可能习惯性地认为 树的⾼度就是 logN，但这并不⼀定。logN 的⾼度只存在于平衡⼆叉树，对于⼀般的树可能出现极端不平衡的情况，使得「树」⼏乎退化成「链表」，树的⾼度最坏情况下可能变成 N。
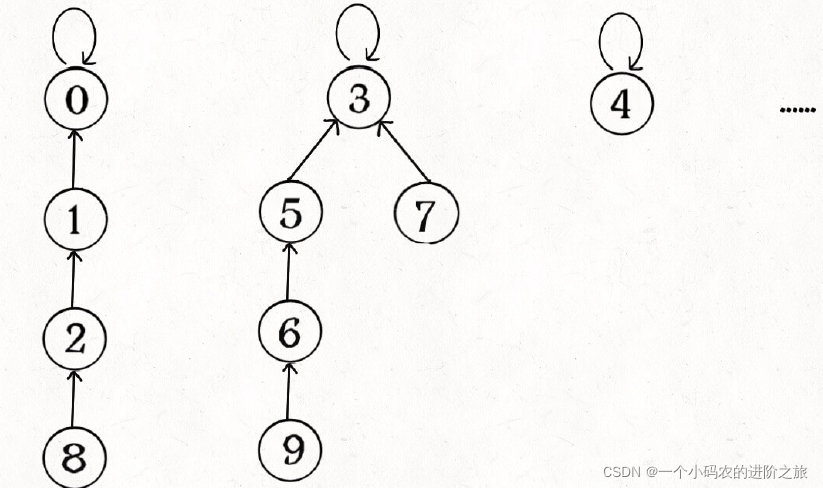
在这里插入图片描述
所以说上⾯这种解法，find , union , connected 的时间复杂度都是 O(N)。这个复杂度很不理想的，你想图论解决的都是诸如社交⽹络这样数据规模巨⼤的问题，对于 union 和 connected 的调⽤⾮常频繁， 每次调⽤需要线性时间完全不可忍受。

问题的关键在于，如何想办法避免树的不平衡呢？只需要略施⼩计即可。

性能优化 之 平衡性优化

我们要知道哪种情况下可能出现不平衡现象，关键在于 union 过程：

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // 将两棵树合并为⼀棵
    parent[rootP] = rootQ;
    // parent[rootQ] = rootP 也⼀样
    count--; // 两个分量合⼆为⼀
}

我们⼀开始就是简单粗暴的把 p 所在的树接到 q 所在的树的根节点下⾯，那么这⾥就可能出现 「头重脚轻」 的不平衡状况，⽐如下⾯这种局⾯：
在这里插入图片描述
⻓此以往，树可能⽣⻓得很不平衡。我们其实是希望，⼩⼀些的树接到⼤⼀些的树下⾯，这样就能避免头重脚轻，更平衡⼀些 。解决⽅法是额外使⽤⼀个 size 数组，记录每棵树包含的节点数，我们不妨称为 「重量」：

class UF {
    private int count;
    private int[] parent;
    // 新增⼀个数组记录树的“重量”
    private int[] size;
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        // 最初每棵树只有⼀个节点
        // 重量应该初始化 1
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    /* 其他函数 */
}

⽐如说 size[3] = 5 表示，以节点 3 为根的那棵树，总共有 5 个节点。这样我们可以修改⼀下 union ⽅法：

public void union(int p, int q) {
    int rootP = find(p);
    int rootQ = find(q);
    if (rootP == rootQ)
        return;
    // ⼩树接到⼤树下⾯，较平衡
    if (size[rootP] > size[rootQ]) {
        parent[rootQ] = rootP;
        size[rootP] += size[rootQ];
    } else {
        parent[rootP] = rootQ;
        size[rootQ] += size[rootP];
    }
    count--;
}

这样，通过⽐较树的重量，就可以保证树的⽣⻓相对平衡，树的⾼度⼤致在 logN 这个数量级，极⼤提升执⾏效率。

此时，find , union , connected 的时间复杂度都下降为 O(logN)，即便数据规模上亿，所需时间也⾮常少。

性能优化 之 路径压缩 TODO

这步优化特别简单，所以⾮常巧妙。我们能不能进⼀步压缩每棵树的⾼度，使树⾼始终保持为常数？
在这里插入图片描述
这样 find 就能以 O(1) 的时间找到某⼀节点的根节点，相应的，connected 和 union 复杂度都下降为O(1)。

要做到这⼀点，⾮常简单，只需要在 find 中加⼀⾏代码：

private int find(int x) {
    while (parent[x] != x) {
        // 进⾏路径压缩
        parent[x] = parent[parent[x]];
        x = parent[x];
    }
    return x;
}

调⽤ find 函数每次向树根遍历的同时，顺⼿将树⾼缩短了，最终所有树⾼都不会超过 3（union 的时候树⾼可能达到 3）。

完整代码 & 时间复杂度最终分析

class UF {
    // 连通分量个数
    private int count;
    // 存储⼀棵树
    private int[] parent;
    // 记录树的「重量」
    private int[] size;
    // n 为图中节点的个数
    public UF(int n) {
        this.count = n;
        parent = new int[n];
        size = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i;
            size[i] = 1;
        }
    }
    // 将节点 p 和节点 q 连通
    public void union(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        if (rootP == rootQ)
            return;
        // ⼩树接到⼤树下⾯，较平衡
        if (size[rootP] > size[rootQ]) {
            parent[rootQ] = rootP;
            size[rootP] += size[rootQ];
        } else {
            parent[rootP] = rootQ;
            size[rootQ] += size[rootP];
        }
        // 两个连通分量合并成⼀个连通分量
        count--;
    }
    // 判断节点 p 和节点 q 是否连通
    public boolean connected(int p, int q) {
        int rootP = find(p);
        int rootQ = find(q);
        return rootP == rootQ;
    }
    // 返回节点 x 的连通分量根节点
    private int find(int x) {
        while (parent[x] != x) {
            // 进⾏路径压缩
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    // 返回图中的连通分量个数
    public int count() {
        return count;
    }
}

Union-Find 算法的复杂度可以这样分析：构造函数初始化数据结构需要 O(N) 的时间和空间复杂度；连通两个节点 union、判断两个节点的连通性 connected、计算连通分量 count 所需的时间复杂度均为 O(1) 。

2 经典算法 之 朋友圈问题

班上有 N 名学生。其中有些人是朋友，有些则不是。他们的友谊具有是传递性。如果已知 A 是 B 的朋友，B 是 C 的朋友，那么我们可以认为 A 也是 C 的朋友。所谓的朋友圈，是指所有朋友的集合。
给定一个 N * N 的矩阵 M，表示班级中学生之间的朋友关系。如果M[i][j] = 1，表示已知第 i 个和 j 个学生互为朋友关系，否则为不知道。你必须输出所有学生中的已知的朋友圈总数。

解题思路：这是一个典型的并查集的问题，将朋友圈中，是朋友的人加入一个并查集。在初始情况下，所有人都不是朋友，则朋友圈的数量就是人的总数，每当检测到两个朋友不在一个并查集，那么就将其加入一个并查集，然后朋友圈的总数减一。

// 经典算法题 之 朋友圈
public int findCircleNum(int[][] M) {
    // 1.初始化父节点，将其指向自己
    int n = M.length;
    int[] parent = new int[n];
    for (int i = 0; i < n; i++) {
        parent[i] = i;
    }
    /*
    用List也可以
    List<Integer> parent = new ArrayList<>();
    for(int i = 0; i < n; i++){
        parent.add(i);
    }
     */
    // 在初始情况下，所有人都不是朋友，则朋友圈的数量就是人的总数
    int result = n;
    // 每当检测到两个朋友不在一个并查集，那么就将其加入一个并查集，
    // 然后朋友圈的总数减一。
    for (int i = 1; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if (M[i][j] == 1) {
                if (find(parent,i) != find(parent,j)) {
                    result--;
                    // 建立并查集
                    union(parent,i,j);
                }
            }
        }
        
    }
    return result;
}
public void union(int[] parent, int index1, int index2) {
    int rootP = find(parent, index1);
    int rootQ = find(parent, index2);
    parent[rootP] = rootQ;
}
public int find(int[] parent,int x) {
    while (parent[x] != x) {
        parent[x] = parent[parent[x]];
        x = parent[x];
    }
    return x;
}
/*
递归写法
public int find(int x) {
    if(x != p.get(x)){
        p.set(x, find(p.get(x)));
    }

    return p.get(x);
}
 */

3 leetcode其它相关题目

130. 被围绕的区域

这个问题不如看成岛屿问题，并查集以后再讲解吧

class Solution {
    public void solve(char[][] board) {
        int m = board.length,n = board[0].length;

        // 剩下的就是
        for (int i = 1; i < m - 1; i++) {
            for (int j = 1; j < n - 1; j++) {
                if (board[i][j] == 'O') {
                    dfs_solve(board,i,j);
                }
            }
        }
    }
    public void dfs_solve(char[][] board,int i,int j) {
        int m = board.length,n = board[0].length;
        if (i < 0 || j < 0 || i >= m || j >= n || board[i][j] == 'X') {
            return;
        }
        board[i][j] = 'X';
        dfs_solve(board,i-1,j);
        dfs_solve(board,i+1,j);
        dfs_solve(board,i,j-1);
        dfs_solve(board,i,j+1);
    }
}

990. 等式方程的可满足性

这个问题⽤ Union-Find 算法就显得⼗分优美了。题目分析：

  • 给你⼀个数组 equations，装着若⼲字符串表示的算式。
  • 每个算式 equations[i] ⻓度都是 4，⽽且只有这两种情况：a==b 或者 a!=b，其中 a,b 可以是任意⼩写字⺟。
  • 你写⼀个算法，如果 equations 中所有算式都不会互相冲突，返回 true，否则返回 false。

之前分析过，，动态连通性其实就是⼀种等价关系，具有「⾃反性」「传递性」和「对称性」，其实 == 关系也是⼀种等价关系，具有这些性质。所以这个问题⽤ Union-Find 算法就很⾃然。

思路分析：

  • 首先将 equations 中的算式根据 == 和 != 分成两部分，先处理 == 算式，使得他们通过相等关系各⾃勾结成⻔派（连通分量）；
  • 然后处理 != 算式，检查不等关系是否破坏了相等关系的连通性。
public class Main {
    // 990. 等式方程的可满足性
    public boolean equationsPossible(String[] equations) {
        // 1.初始化父节点，将其指向自己
        int[] parent = new int[26];
        for (int i = 0; i < 26; i++) {
            parent[i] = i;
        }
        // 2.先让相等的字⺟形成连通分量
        for (String eq : equations) {
            if (eq.charAt(1) == '=') {
                int x = eq.charAt(0) - 'a';
                int y = eq.charAt(3) - 'a';
                union(parent,x,y);
            }
        }
        // 3.检查不等关系是否打破相等关系的连通性
        for (String eq : equations) {
            if (eq.charAt(1) == '!') {
                int x = eq.charAt(0) - 'a';
                int y = eq.charAt(3) - 'a';
                if (find(parent,x) == find(parent,y)) {
                    return false;
                }
            }
        }
        return true;
    }
    public void union(int[] parent, int index1, int index2) {
        int rootP = find(parent, index1);
        int rootQ = find(parent, index2);
        parent[rootP] = rootQ;
    }

    public int find(int[] parent, int index) {
        while (parent[index] != index) {
            parent[index] = parent[parent[index]];
            index = parent[index];
        }
        return index;
    }

}

当然也可以用第一节中的UF类，代码如下：

boolean equationsPossible(String[] equations) {
    // 26 个英⽂字⺟
    UF uf = new UF(26);
    // 先让相等的字⺟形成连通分量
    for (String eq : equations) {
        if (eq.charAt(1) == '=') {
            labuladong 的算法秘籍labuladong的刷题三件套
            294 / 607
            char x = eq.charAt(0);
            char y = eq.charAt(3);
            uf.union(x - 'a', y - 'a');
        }
    }
    // 检查不等关系是否打破相等关系的连通性
    for (String eq : equations) {
        if (eq.charAt(1) == '!') {
            char x = eq.charAt(0);
            char y = eq.charAt(3);
            // 如果相等关系成⽴，就是逻辑冲突
            if (uf.connected(x - 'a', y - 'a'))
                return false;
        }
    }
    return true;
}

547. 省份数量

这个题和朋友圈的思路是一样的，代码如下：

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int[] parent = new int[n];
        int result = n;

        for (int i = 0; i < n; i++) {
            parent[i] = i;
        }
        for (int i = 1; i < n; i++) {
            for (int j = 0; j < i; j++) {
                if (isConnected[i][j] == 1) {
                    if (find(parent,i) != find(parent,j)) {
                        result--;
                        union(parent,i,j);
                    }
                }
            }
        }
        return result;
    }
    public void union(int[] parent, int index1, int index2) {
        int rootP = find(parent, index1);
        int rootQ = find(parent, index2);
        parent[rootP] = rootQ;
    }
    public int find(int[] parent,int x) {
        while (parent[x] != x) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
}
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

熠熠98

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值