【迁移学习】Agile Domain Adaptation——一种平衡运算资源和速度的深度迁移学习方法

Agile Domain Adaptation

背景

在现在的迁移学习工作中，一直有一个矛盾：准确率和运算成本之间的矛盾。在神经网络面对一个个的样本进行分类时，有的样本可能和训练数据非常相似，用很少的层数就可以分类出来，但有的可能和神经网络所见到的训练样本差别比较大，需要提取深层特征才能良好的分类。对于简单目标，进行深度特征提取就比较浪费运算资源了。所以有了这个工作。

领域自适应是迁移学习领域中一个非常热门的方向，其本意是用来解决训练集数据和实际应用时采集的数据的分布不同，导致模式识别系统效果不好，所以需要一类方法来自适应的来适应不同的应用环境。

现阶领域自适应方法大体上可以分成两个种类：传统方法和深度的方法。传统方法着重于迁移技术，比如数据分布的适应。深度的方法一遍着重于特征的提取，另一方面着重于通过端对端的方法来使知识自适应。在这些工作中无论是传统的方法还是深度的方法，都忽略了一个问题是我们不能将目标域中的数据以相同的处理流程来处理。在目标域中不同的数据分布和源域之间的相似性是不同的，数据分布相似的数据更容易被迁移，而数据分布差异较大的部分应当使用更多的运算能力来处理。如图1，有一部分数据和源域数据相似程度很高，我们可以认为数据分布比较相近，另一部分数据相似度较低，则分布相差较大同样分类难度更大。

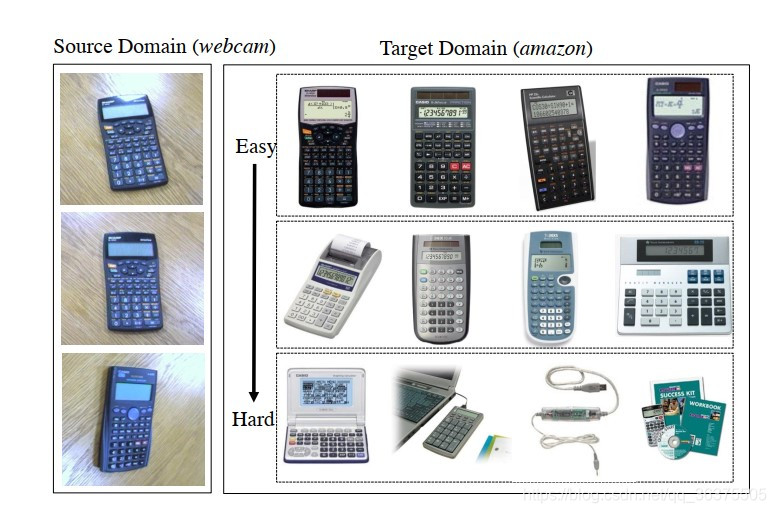
图1

实现

现有的深度学习模型有一个特点，网络浅层的神经结构往往会学习出一些比较泛化局部的特征，而深层的网络往往会学习出比较全局的深层特征，对于相关的深度迁移学习模型也类似（如DAN，Deep adaption Networks），对于二者分布比较相近的数据用比较浅层的模型就可以处理了，对于数据分布差异比较大的数据，可以用整个模型。这种思想考虑到了源域数据和目标域数据之间不同数据的分布差异，而不是把全部的数据都一股脑的送到同一个模型当中。具体结构如图二。

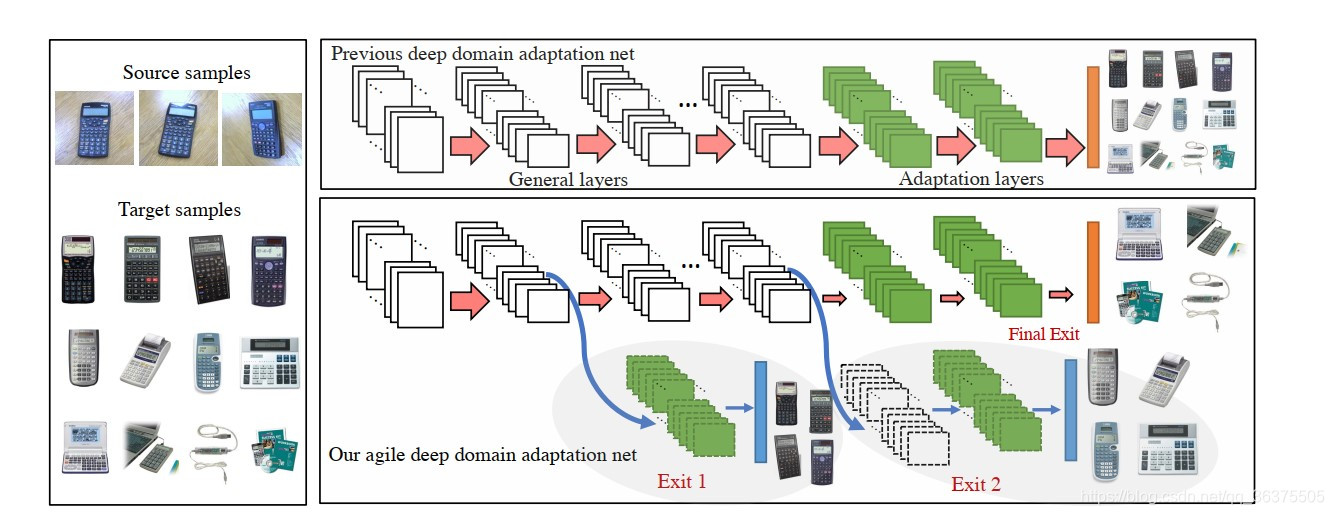
图2
要实现这样一个网络主要需要解决两个问题：

1. 得到一个具有多个出口的深度迁移网络，确定损失函数，同时可以进行正常的训练（可以用BP算法）。
2. 确定一个评价准则，可以在实际应用中知道多个分类输出口哪一个是最优的，到了哪一个出口后面的就不需要在求了。

损失函数确定

在源域上，一个端到端的神经网络训练问题可以有如下的损失函数：
${\mathcal{L}}_{\mathrm{s}\mathrm{u}\mathrm{p}}=\frac{1}{n_s}{\sum }_{i=1}^{n_s}J\left(f\left({\mathbf{x}}_{s,i}\right),{\mathbf{y}}_{s,i}\right)$
这种优化方法，随着损失函数的降低，可以使模型在源域上的效果更好，但是无法使训练出的模型在目标域上有更好的表现，所以需要考虑到源域和目标域的损失情况。
${\mathcal{L}}_{{\text{exit }}_e}={\mathcal{L}}_{\text{sup }}+\lambda {\mathcal{L}}_{\text{tran }}$
和普通模型不同的是，在这个模型中有多个输出分类，所以需要考虑每一个端的优化问题。
$\mathcal{L}={\sum }_{ϵ=1}^m{w}_{ϵ}{\mathcal{L}}_{{\mathrm{e}\mathrm{x}\mathrm{i}\mathrm{t}}_{ϵ}}$
整体的损失函数形式就如上面所示，在实际中w可以都变成1，这可以认为是对每一个出口的重视程度都相同。
上面只是形式化了整个损失函数的结构。在这个工作当中，损失函数具体使用的是cross-entropy。
$J(\hat{\mathbf{y}},\mathbf{y})=-\frac{1}{|C|}{\sum }_{c\in C}{y}_c\log {\hat{y}}_c$
其中$\hat{\mathbf{y}}$是预测结果。
$\hat{\mathbf{y}}=\mathrm{softmax}(f(\mathbf{x}))=\frac{\exp (f(\mathbf{x}))}{{\sum }_{c\in C}\exp \left(f(\mathbf{x}{)}_c\right)}$
在这里，使用cross-entropy是经过深思熟虑的，这种方法的特性使得后面可以很好的区分哪一个出口的数据已经足够好不需要继续求解下面的出口了。
在迁移学习的部分，迁移部分的损失采用多核MMD。定义如下：
$\begin{array}{rl}\mathrm{MMD}\left({\mathbf{X}}_s,{\mathbf{X}}_t\right)& =\frac{1}{n_s^2}\sum _{i=1}^{n_s}\sum _{j=1}^{n_s}k\left({\mathbf{x}}_{s,i},{\mathbf{x}}_{s,j}\right)\\ -& \frac{2}{n_s{n}_t}\sum _{i=1}^{n_s}\sum _{j=1}^{n_t}k\left({\mathbf{x}}_{s,i},{\mathbf{x}}_{t,j}\right)\\ & +\frac{1}{n_t^2}\sum _{i=1}^{n_s}\sum _{j=1}^{n_s}k\left({\mathbf{x}}_{t,i},{\mathbf{x}}_{t,j}\right)\end{array}$
其中$k(\cdot )$是希尔伯特核。
原始数据特征x上计算MMD，而最小化上式在匹配域自适应层生成的激活时是隐含的。在迁移学习中，鼓励域适应层生成的源激活和目标激活保持良好的对齐，以便层参数可以由两个域共享。因此，这里显式地最小化了层激活上的MMD 设${\mathbf{Z}}_s^l$和${\mathbf{Z}}_t^l$分别表示层l从源域和目标域生成的激活量，层激活量的MMD计算公式为:
$\begin{array}{rl}{\mathcal{L}}_{\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{n}}& =\frac{1}{n_s^2}\sum _{i=1}^{n_s}\sum _{j=1}^{n_s}\prod _{l=1}^L{k}^l\left({\mathbf{z}}_{s,i}^l,{\mathbf{z}}_{s,j}^l\right)\\ & -\frac{2}{n_s{n}_t}\sum _{i=1}^{n_s}\sum _{j=1}^{n_t}\prod _{l=1}^L{k}^l\left({\mathbf{z}}_{s,i}^l,{\mathbf{z}}_{t,j}^l\right)\\ & +\frac{1}{n_t^2}\sum _{i=1}^{n_s}\sum _{j=1}^{n_s}\prod _{l=1}^L{k}^l\left({\mathbf{z}}_{t,i}^l,{\mathbf{z}}_{t,j}^l\right)\end{array}$
等价于：
$\begin{array}{c}{\mathcal{L}}_{\mathrm{tran}}=\\ \frac{2}{n_s}{\sum }_{i=1}^{n_s/2}\left({\prod }_{l=1}^L{k}^l\left({\mathbf{z}}_{s,2i-1}^l,{\mathbf{z}}_{s,2i}^l\right)+{\prod }_{l=1}^L{k}^l\left({\mathbf{z}}_{t,2i-1}^l,{\mathbf{z}}_{t,2i}^l\right)\right)\\ -\frac{2}{n_s}{\sum }_{i=1}^{n_s/2}\left({\prod }_{l=1}^L{k}^l\left({\mathbf{z}}_{s,2i-1}^l,{\mathbf{z}}_{t,2i}^l\right)+{\prod }_{l=1}^L{k}^l\left({\mathbf{z}}_{t,2i-1}^l,{\mathbf{z}}_{s,2i}^l\right)\right)\end{array}$
计算过程如下: