Lecture03: Harmonic Analysis of Deep Convolutional Neural Networks

STATS385

Lecture03: Harmonic Analysis of Deep Convolutional Neural Networks

• 深度学习在ImageNet图像分类、image captioning的成绩；
• 图像分类的一般步骤：特征提取+线性分类器。对于线性不可分的数据，需要用非线性特征提取；
• 图像分类的要求：translation invariance, deformation insensitivity；
• Scattering network在设计时就考虑了这两点并将这种机制融入到模型本身中，并没有利用滤波、非线性和pooling的操作（课件有问题？）。其结构如下图所示
  
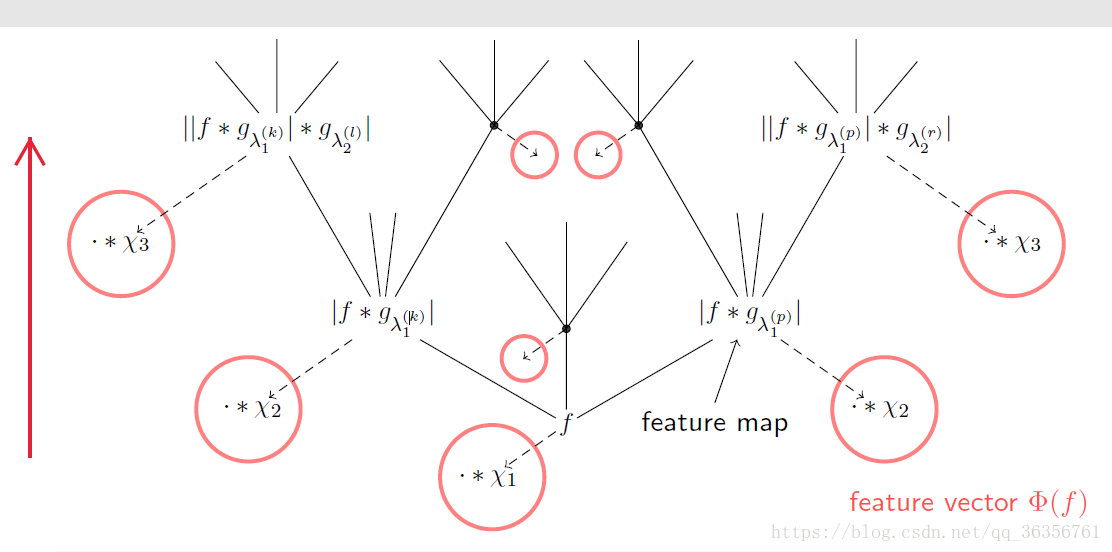
  $f$ 代表输入图像。该模型自底向上传播，在每一个节点都扩散到若干个子节点。每一个节点都进行一个卷积-求模（绝对值）-卷积操作。抽象出来就是滤波-非线性-pooling，如下图所示
  
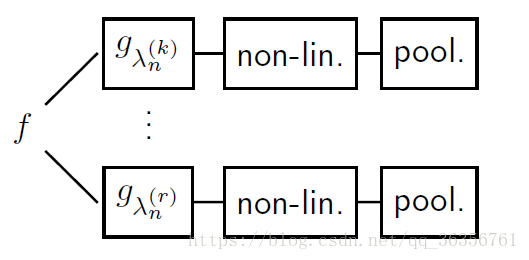
  这样，每个节点的输出再与$\chi_n$进行卷积，就得到了相应层的feature。
  由Parseval定理知，这些滤波器满足
  $\exists A_n, B_n > 0, \quad\mathrm{s.t.} A_n\lVert f \rVert^2_2 \le \lVert f*\chi_n \rVert^2_2 + \underset{\lambda_n \in \Lambda_n}{\sum} \lVert f * g_{\lambda_n} \rVert^2_2 \le B_n\lVert f \rVert^2_2$
  而这些point-wise非线性函数应满足Lipschitz-continuous条件，即
  $\lVert M_n(f) - M_n(h) \rVert_2 \le L_n\lVert f - h \rVert,\quad \forall f,h \in L^2(\mathbb{R}^d)$
  而该条件是能被现如今几乎所有被应用在深度学习中的非线性函数所满足的，如对于ReLU，$L_n = 1$，对于sigmoid，$L_n = \frac{1}{4}$（易证）
  对于pooling层而言，满足
  $f \mapsto S^{d/2}_nP_n(f)(S_n\cdot)$
  即先对图像$f$ 进行$P_n$变换，然后对变换后的图像坐标进行尺度为$S_n$ 的伸缩，最后乘上一个系数，其中pooling factor $S_n \ge 1, Pn:L^2(\mathbb{R}^d) \to L^2(\mathbb{R}^d)$ 是$R_n$-Lipschitz连续的。无独有偶，该条件也能被大部分现行的深度网络中的pooling层满足，如降采样层满足$P_n(f) = f, R_n = 1$，max pooling层满足$P_n(f) = f * \phi_n, R_n = \lVert \phi_n \rVert_1, \phi_n = \mathrm{ones()}$
  关于垂直平移不变性有如下定理
  $\mathrm{Theorem}$ 假设滤波器、非线性函数和pooling层满足$B_n \le \min \{1,L_n^{-2}R_n^{-2}\}, S_n \ge 1, \forall n \in \mathbb{N}$，则$\lVert \Phi^n(T_tf) - \Phi^n(f) \rVert = O(\frac{\lVert t \rVert}{\underset{1 \le i \le n}{\prod}S_i}) \quad \forall f \in L^2(\mathbb{R}^d), t \in \mathbb{R}^d, n \in \mathbb{N}$
  即越是深层的pooling层，其特征受到垂直平移算子$T_t$ 的影响就越小，这就从理论上保证了scattering network对输入的垂直平移不变性。而该定理的前提条件也很容易满足，只要对滤波器进行归一化就行了。另外水平平移不变性也有类似的定理。
  非线性变换/算子：$F_\tau f = f(x - \tau(x)), \tau \in \mathbb{R}^d \to \mathbb{R}^d$。对于给定的非线性变换，变形的程度与函数$f$ 有很大的关系
  变形稳定性边界
  $\lVert \Phi_W(F_\tau f) - \Phi_W(f) \rVert \le C(2^{-J}\lVert \tau \rVert_\infty + J\lVert D\tau \rVert_\infty + \lVert D^2\tau \rVert_\infty)\lVert f \rVert_W,\quad \forall f \in H_W \subset L^2(\mathbb{R}^d)$，其中$W$ 是小波。该式表明，对于小的形变，图像的特征不会有较大的变化。
• CNN
  非线性函数为求模函数的卷积层具有解调效应
  
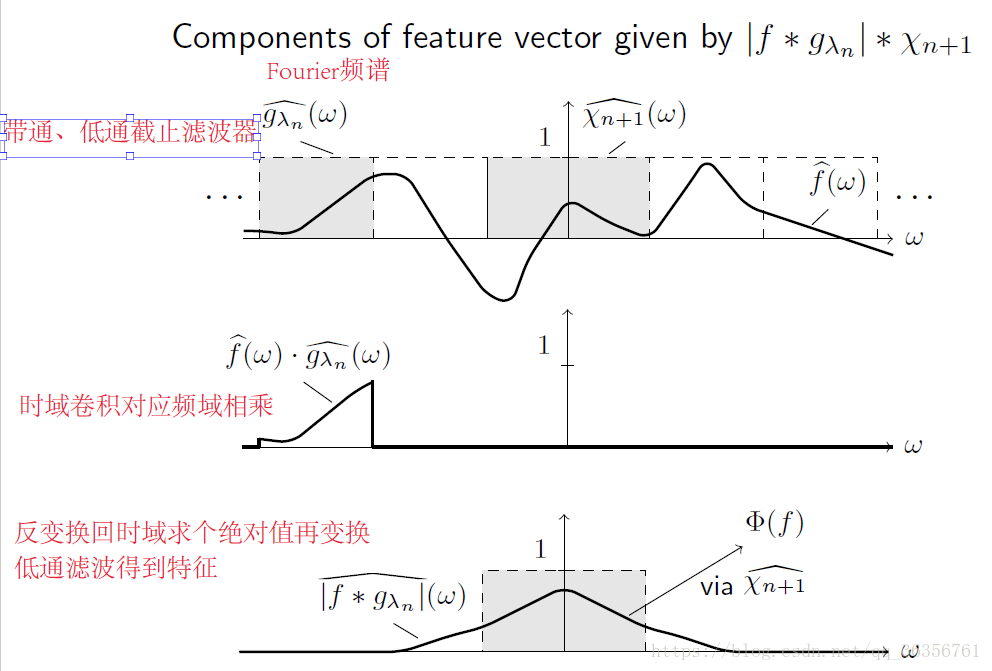
  那所有的非线性函数都有解调功能吗？对于求模函数当然如此；对于模平方函数则更是如此，而且它的高频抑制更强，但是该函数不是Lipschitz连续的；而对于ReLU函数则不是。
  接下来我们重点讨论以下4个问题：
  1、Determine how fast the energy contained in the propagated signals (a.k.a. feature maps) decays across layers.
  首先对滤波器进行一些假设：1、滤波器是解析的，即$\exists \mathbb{R}^d$ 的一个超卦限（不必正则）$H_{\lambda_n}$ 使得$\mathrm{supp}(\widehat{g_{\lambda_n}}) \subset H_{\lambda_n}$；2、滤波器是高通的。这两个条件包含了大部分的WH(Weyl-Heisenberg)滤波器、小波等
  再介绍一个概念——$s$阶Sobolev函数：
  $H^s(\mathbb{R}^d) = \{f \in L^2(\mathbb{R}^d)|\int_{\mathbb{R}^d}(1 + \lvert \omega \rvert^2)^s \lvert \hat{f}(\omega)\rvert^2\mathrm{d}\omega < \infty\}, s\ge 0$。大部分信号都符合该条件。
  这样就能得到对于小波滤波器和WH滤波器，每一层特征的能量随着模型深度指数衰减的定理，并且信号越光滑、pooling层降采样率越大，特征的能量衰减越快。而对于一般的滤波器，则为多项式衰减。
  2、Guarantee trivial null-space for feature extractor $\Phi$
  $\Phi$ 具有简单零空间指$\Phi(x) = 0 \Leftrightarrow x = 0$。否则后续的线性分类器将在其非零零点处不可分。
  为了满足该条件，$\Phi$ 应该满足$\exists A,B>0, \mathrm{s.t.} A\lVert f \rVert^2_2 \le \lVert \Phi(f) \rVert^2_2 \le B\lVert f \rVert^2_2$
  “能量守恒”：所有层信号特征的能量是和信号本身的能量同级别的（$\Theta(\cdot)$）。由此也可以得到1中特征能量对深度衰减到0的结论。
  3、Specify the number of layers needed to have “most” of the input signal energy be contained in the feature vector
  定理表明，为了在一定程度上保持所有层特征的能量，模型的深度不能小于某个阈值。同时这也保证了每一层的$\Phi$ 的简单零空间性质，因为后面加上去的每一层都是有能量的，这样就避免特征函数在非零处取零的情况。
  由于一般的滤波器的特征能量是多项式级别衰减的，所以为了保持相同的信号能量，由一般的滤波器构成的模型需要的深度比小波或WH滤波器的大。回忆ResNet152，对于小波和WH滤波器而言，只需要11层和14层就够了。
  4、For a fi xed (possibly small) depth, design CNNs that capture “most” of the input signal energy
  定理表明，要想降低模型的深度，必须增加第一层特征的channel数，这是depth-width之间的一种trade-off。
  最后，作者还给出了在MNIST上的测试结果，结果表明求模运算和ReLU比tanh和logsig性能要好，而且加pooling层的效果和不加pooling效果相当，但是显著降低了计算量。但是最近的模型都在往有方向、不可分小波、去pooling和更高的计算复杂度的趋势发展。