统计指标函数
返回最大值和最小值所在位置
平均值,中位数,方差

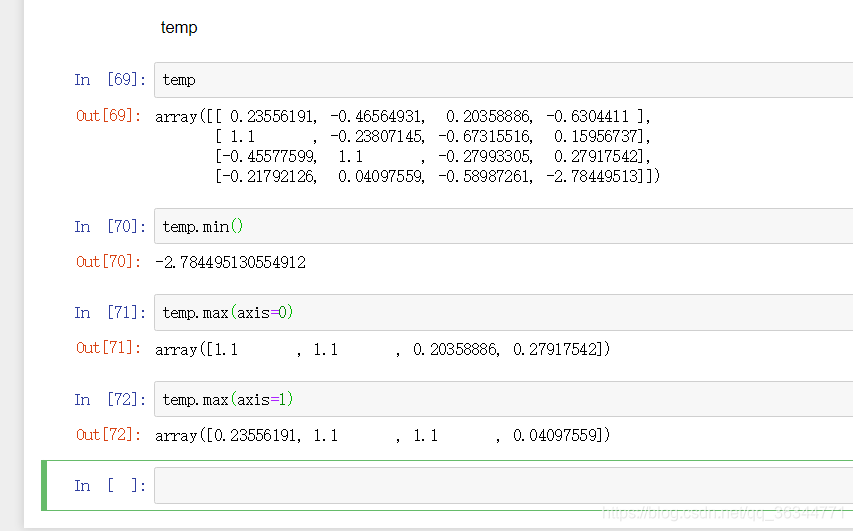
axis=0是按列
axis=1是按行
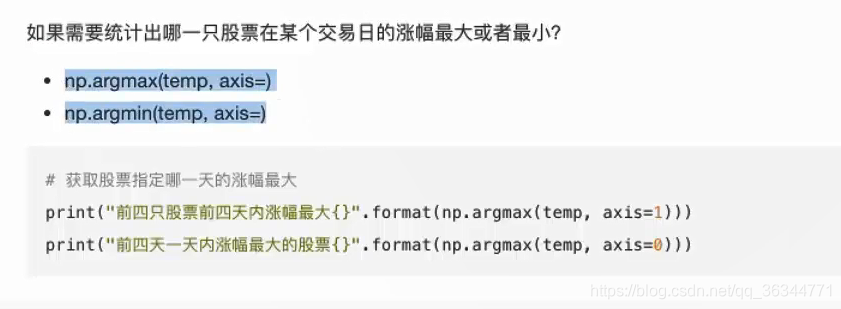
最大值和最小值的位置
20190717——ndarray统计运算
最新推荐文章于 2025-06-29 16:46:39 发布
统计指标函数
返回最大值和最小值所在位置
平均值,中位数,方差


axis=0是按列
axis=1是按行

最大值和最小值的位置
 1532
1532
 655
655

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


