正则表达式匹配(动态回归系列)

最新推荐文章于 2022-11-13 21:04:25 发布

原创最新推荐文章于 2022-11-13 21:04:25 发布 · 844 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#动态回归

leetcode 专栏收录该内容

1 篇文章

订阅专栏

这篇博客详细介绍了如何使用动态规划解决正则表达式匹配问题，包括回溯、自顶向下、自底向上三种方法的思路和代码实现。重点讨论了动态规划的转移方程和状态初始化。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

一、题目描述
二、AC方法

一、题目描述

题目来源：https://leetcode-cn.com/problems/regular-expression-matching

给你一个字符串 s 和一个字符规律 p，请你来实现一个支持 ‘.’ 和 ‘*’ 的正则表达式匹配。

'.' 匹配任意单个字符
'*' 匹配零个或多个前面的那一个元素
所谓匹配，是要涵盖 整个 字符串 s的，而不是部分字符串。

说明:

s 可能为空，且只包含从 a-z 的小写字母。
p 可能为空，且只包含从 a-z 的小写字母，以及字符 . 和 *。

示例 1:

输入:
s = "aa"
p = "a"
输出: false
解释: "a" 无法匹配 "aa" 整个字符串。

示例 2:

输入:
s = "aa"
p = "a*"
输出: true
解释: 因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。

示例 3:

输入:
s = "ab"
p = ".*"
输出: true
解释: ".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

示例 4:

输入:
s = "aab"
p = "c*a*b"
输出: true
解释: 因为 '*' 表示零个或多个，这里 'c' 为 0 个, 'a' 被重复一次。因此可以匹配字符串 "aab"。

示例 5:

输入:
s = "mississippi"
p = "mis*is*p*."
输出: false

二、AC方法

1. 回溯（递归解法）

public static boolean isMatch(String s, String p) {
        if (p.isEmpty()) {
            return s.isEmpty();
        }
        boolean firstMatch = (!s.isEmpty() && (p.charAt(0) == s.charAt(0) || p.charAt(0) == '.'));
        //一种是匹配0个，那么只需要跳过p中的这两个字符，继续与s中的字符进行比较即可，
        // 如果是匹配多个(那么第一个必须也匹配)，那么将s中的游标往后移动一个，继续进行判断，这两个条件只要其中一个能满足即可。
        if (p.length() > 1 && p.charAt(1) == '*') {
            //匹配0个，则只需要跳过p,p移动2位，s保持不变(不需要firstMatch)
            //匹配多个，则p保持不变，p的光标还是保持在0位，s移动下一位（同时要求第一位也必须匹配即firstMatch）
            return (isMatch(s, p.substring(2)) || firstMatch && isMatch(s.substring(1), p));
        } else {
            //如果不是"*"，则要求当前的第一个字符必须匹配，然后在下一个字符匹配
            return firstMatch && isMatch(s.substring(1), p.substring(1));
        }
    }

2. 自顶向下

参考：https://www.imooc.com/article/281353?block_id=tuijian_wz

2.1 思路过程

假定使用符号:
s[i:] 表示字符串s中从第i个字符到最后一个字符组成的子串；
p[j:] 表示模式串p中，从第j个字符到最后一个字符组成的子串；
match(i,j) 表示s[i:]与p[j:]的匹配情况，如果能匹配，则置为true，否则置为false。这就是各个子问题的状态。
那么对于match(i,j)的值，取决于p[j + 1]是否为’*’。

curMatch = i < s.length() && s[i] == p[j] || p[j] == ‘.’;
p[j + 1] != ‘*’，match(i,j) = curMatch && match(i + 1, j + 1)
p[j + 1] == ‘*’，match(i,j) = match(i, j + 2) || curMatch && match(i + 1, j)

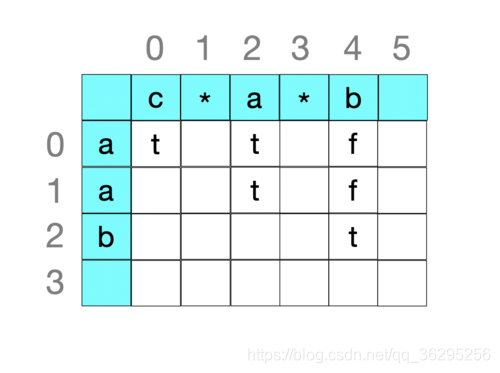
以s = “aab”; p = "cab"为例，先构建一个二维状态空间来存储中间计算得出的状态值。横向的值代表i，纵向的值代表j，match(0,0)的值即问题的解，用f代表false，t代表true

2.2 推算过程

求match(0,0): i = 0; j = 0; curMatch = false;

p[1] == * -> match(0,0) = match(0,2) || false && match(1,0)

转化为求子问题match(0,2)和match(1,0)

求match(0,2): i = 0; j = 2; curMatch = true;

p[1] == * -> match(0,2) = match(0,4) || true && match(1,2)

求match(0,4): i = 0; j = 4; curMatch = false;

j + 1 == 5 >= p.length() -> match(0,4) = curMatch = false;

match(0,4) = false;

回溯到第五步，求match(1,2): i = 1; j = 2; curMatch = true;

p[3] == * -> match(1,2) = match(1,4) || true && match(2,2)

求match(1,4): i = 1; j = 4; curMatch = false;

j + 1 == 5 >= p.length() -> match(1,4) = curMatch = false;

match(1,4) = false;

回溯到第10步，求match(2,2): i = 2; j = 2; curMatch = false;

p[3] == * -> match(2,2) = match(2,4) || false && match(3,2)

求match(2,4): i = 2; j = 4; curMatch = true;

j + 1 == 5 >= p.length() -> match(2,4) = curMatch = true;

match(2,4) = true;

回溯到第15步。

match(2,2) = true;

回溯到第10步。

match(1,2) = true;

回溯到第5步。

match(0,2) = true;

回溯到第2步。

match(0,0) = true;

问题解决

2.3 代码

class Solution {
    Result[][] memo;

    public boolean isMatch(String text, String pattern) {
        memo = new Result[text.length() + 1][pattern.length() + 1];
        return dp(0, 0, text, pattern);
    }

    public boolean dp(int i, int j, String text, String pattern) {
        if (memo[i][j] != null) {
            return memo[i][j] == Result.TRUE;
        }
        boolean ans;
        if (j == pattern.length()){
            ans = i == text.length();
        } else{
            boolean first_match = (i < text.length() &&
                                   (pattern.charAt(j) == text.charAt(i) ||
                                    pattern.charAt(j) == '.'));

            if (j + 1 < pattern.length() && pattern.charAt(j+1) == '*'){
                ans = (dp(i, j+2, text, pattern) ||
                       first_match && dp(i+1, j, text, pattern));
            } else {
                ans = first_match && dp(i+1, j+1, text, pattern);
            }
        }
        memo[i][j] = ans ? Result.TRUE : Result.FALSE;
        return ans;
    }
}

3. 自底向上

3.1思路

其实很简单粗暴，即从最后一个字符开始反向匹配，还是以刚才的栗子为例，从i = 3, j = 5 开始依次往左往上循环计算，match(3,5) == true，核心的逻辑并没有变。因为最边缘的值的匹配都是可以直接计算出来的

3.2 代码

class Solution {
    public boolean isMatch(String text, String pattern) {
        boolean[][] memo = new boolean[text.length() + 1][pattern.length() + 1];
        memo[text.length()][pattern.length()] = true;

        for (int i = text.length(); i >= 0; i--){
            for (int j = pattern.length() - 1; j >= 0; j--){
                boolean curMatch = (i < text.length() &&
                                       (pattern.charAt(j) == text.charAt(i) ||
                                        pattern.charAt(j) == '.'));
                if (j + 1 < pattern.length() && pattern.charAt(j+1) == '*'){
                    memo[i][j] = memo[i][j+2] || curMatch && memo[i+1][j];
                } else {
                    memo[i][j] = curMatch && memo[i+1][j+1];
                }
            }
        }
        return memo[0][0];
    }
}

4. 动态规划

4.1 状态

f[i][j]表示s1的前i个字符，和s2的前j个字符，能否匹配

4.2 转移方程

如果s1的第 i 个字符和s2的第 j 个字符相同，或者s2的第 j 个字符为 “.”
f[i][j] = f[i - 1][j - 1]
如果s2的第 j 个字符为 *
若s2的第 j 个字符匹配 0 次第 j - 1 个字符
f[i][j] = f[i][j - 2] 比如(ab, abc*)
若s2的第 j 个字符匹配至少 1 次第 j - 1 个字符,
f[i][j] = f[i - 1][j] and s1[i] == s2[j - 1] or s[j - 1] == '.'
这里注意不是 f[i - 1][j - 1]， 举个例子就明白了 (abbb, ab*) f[4][3] = f[3][3]

4.3 初始化

f[0][i] = f[0][i - 2] && s2[i] == *
即s1的前0个字符和s2的前i个字符能否匹配

4.4 结果

f[m][n]

4.5 代码

 public static boolean isMatch1(String s, String p) {
        int m = s.length(), n = p.length();
        //因为匹配是从0开始，到最后字符长度m(n)时，所以是m+1(n+1)
        boolean[][] f = new boolean[m + 1][n + 1];

        f[0][0] = true;
        for(int i = 2; i <= n; i++){
            //s1的前0个字符和s2的前i个字符能否匹配(只有当p的前一个字符为*时才匹配，*可以匹配前面的0个)
            f[0][i] = f[0][i - 2] && p.charAt(i-1) == '*';
        }

        for(int i = 1; i <= m; i++){
            for(int j = 1; j <= n; j++){
                if(s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.'){
                    f[i][j] = f[i - 1][j - 1];
                }
                if(p.charAt(j - 1) == '*'){
                    f[i][j] = f[i][j - 2] ||
                            f[i - 1][j] && (s.charAt(i - 1) == p.charAt(j - 2) || p.charAt(j - 2) == '.');
                }
            }
        }
        return f[m][n];
    }