自己对PID一些学习总结

前言

最近在学习关于PID的一些知识，记录一下。

前期准备

• MATALAB R2020b

过程

pid的基础

PID即：Proportional（比例）、Integral（积分）、Differential（微分）的缩写。顾名思义，PID控制算法是结合比例、积分和微分三种环节于一体的控制算法，它是连续系统中技术最为成熟、应用最为广泛的一种控制算法。PID控制的实质就是根据期望与测量的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出，使得被控对象保持在一个稳定状态。

系统由PID控制器和被控对象组成，原理框图如下

误差$$e(t)=r(t)-u(t)$$

连续控制系统的理想PID控制规律为：
$$u(t)=K_p\left(e(t)+\frac{1}{T_i}{\int }_0^{t}e(t)dt+T_d\frac{de(t)}{dt}\right).$$
式中
$K_p$---- 控制器增益，比例系数，与比例度成倒数关系
$T_i$------积分时间常数
$T_d$------微分时间常数
$e(t)$------期望值与测量值之差

$k_p$—成比例地反映控制系统的偏差信号，偏差一旦产生，立即产生控制作用以减小偏差（图中的 $K_p$，等同）

$k_i$—主要用于消除静差提高系统的无差度。积分作用的强弱，取决于积分时间常数 $Ti$，$Ti$越大积分作用越弱，反之则越强（图中的 $\frac{K_p}{T_i}$）

$k_d$—微分环节的作用能反映偏差信号的变化趋势（变化速率），并能在偏差信号的值变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减小调节时间（图中的 $K_p\cdot T_d$）

比例控制

利用matlab仿真来观察各个系数对曲线的影响，首先，搭建模型，将$k_i，k_d=0$，如下图

仿真结果如下图

从仿真图中可以看出，比例系数$k_p$越小，控制作用越小，系统响应越慢；反之，比例系数$k_p$越大，控制作用也越强，系统响应也越快。它能迅速反映偏差，从而减小偏差，但不能消除静差（静差是指系统控制过程趋于稳定时，给定值与输出量的实测值之差）。但是，$k_p$过大会使系统产生较大的超调和振荡，导致系统的稳定性能变差。

比例控制具有抗干扰能力强、控制及时、过渡时间短的优点，但存在稳态误差，增大比例系数可提高系统的开环增益，减小系统的稳态误差，从而提高系统的控制精度，但这会降低系统的相对稳定性，甚至可能造成闭环系统的不稳定，因此，在系统校正和设计中，比例控制一般不单独使用。
说到可提高系统的开环增益，就要看下图，$K$就是开环增益，而$k_p\cdot K$提高了原本的开环增益，使得分母增大，进而减小稳态误差。

那为什么$k_p$过大会使系统产生较大的超调和振荡，导致系统的稳定性能变差呢？
我们先来看看模型中的根轨迹，如下图所示

num = [1] %开环传递函数的分子多项式
den = [6 5 1] %开环传递函数的分母多项式
sys = tf(num,den)
rlocus(sys) %绘制根轨迹

从图中可以看出，系统的极点都在s平面的左半平面（特征根具有负实部），根据线性系统稳定的充分必要条件可知，系统是稳定的，也就是说最后响应曲线能稳定在某一个值上，但是如何到达稳定，就得具体分析。
我们可以看到系统传递函数只有比例作用时的传递函数$$Gk(s)=\frac{k_p}{(3s+1)(2s+1)}，H(s)=1$$
闭环传递函数$$\Phi (s)=\frac{k_p}{6s^2+5s+k_p+1}$$
可以看出，因为不是标准的二阶系统，可以拆成比例环节乘以震荡环节，也就是把分子$k_p$提出来，$$\Phi (s)=\frac{k_p}{k_p+1}\cdot \frac{\frac{k_p+1}{6}}{s^2+\frac{5s}{6}+\frac{k_p+1}{6}}$$
所以二阶系统的阻尼比$\zeta =\frac{5\sqrt{6}}{12\sqrt{k_p+1}}$，${\omega }_n=\sqrt{\frac{k_p+1}{6}}$
很明显，将$k_p$代入，我们可以得到阻尼比是小于1的，也就是欠阻尼。而欠阻尼系统的响应是有超调的，而且随着阻尼比越小，超调越大，上升时间越短。所以$k_p$越大，阻尼比越小，所以不能一直提高$k_p$的值。

我们也可以从上面那个根轨迹图来判断，首先，我们知道根轨迹是开环系统某一参数从零变到无穷时，闭环系统特征方程式的根在s平面上变化的轨迹。

从图中看出，临界阻尼和过阻尼都是在实轴上，而欠阻尼却变成了共轭复根，根据根轨迹图，当$k_p$（或开环增益）继续增大，那么根轨迹就会往共轭复根处跑，也就会成为欠阻尼了，而且越远离实轴，阻尼比也就越小，超调也会越大。

积分控制

从图中可以看出仅凭$k_p$是不能将曲线调到预定位置，而是和期望值始终有一个稳定的偏差，所以我们需要加上积分系数$k_i$，用来进行无差调节，如下图所示

从图中可以看出，随着$k_i$增大，曲线响应速度加快，产生的超调增大。
加入积分控制后，消除了系统稳态误差，但随着$T_i$值的增大，达到稳态的过渡时间也逐渐加长。

积分项对误差取决于时间的积分，随着时间的增加，积分项会增大。这样，即使误差很小，积分项也会随着时间的增加而加大，它推动控制器的输出增大，使稳态误差进一步减小，直到等于零，但会使系统稳定性降低，过渡时间也加长。

我们可以看到公式中的$\frac{K_p}{T_i}$，积分作用的强弱，取决于积分时间常数 $T_i$，$T_i$越大积分作用越弱，反之则越强。又可以从图中看出，$k_p$同样的情况下，由式子$k_i=\frac{K_p}{T_i}$，$k_i$越大，说明$T_i$越小，积分作用越强，超调越大。所以增大积分时间$T_i$有利于减小超调，减小振荡，使系统的稳定性增加，但是系统静差消除时间变长（$k_i=0.1$）。图中的$k_i=1.2$减少了积分时间，发生了超调，系统出现振荡而且静差消除时间变长。
(补充:单独用积分控制可以提高系统的型别，有利于系统稳态性能的提高，但积分控制使系统增加了一个位于原点的开环极点，使信号产生90°的相角滞后，减少了系统的相角裕度，于系统的稳定性不利。)

微分控制

在调节微分环节的时候，如下图

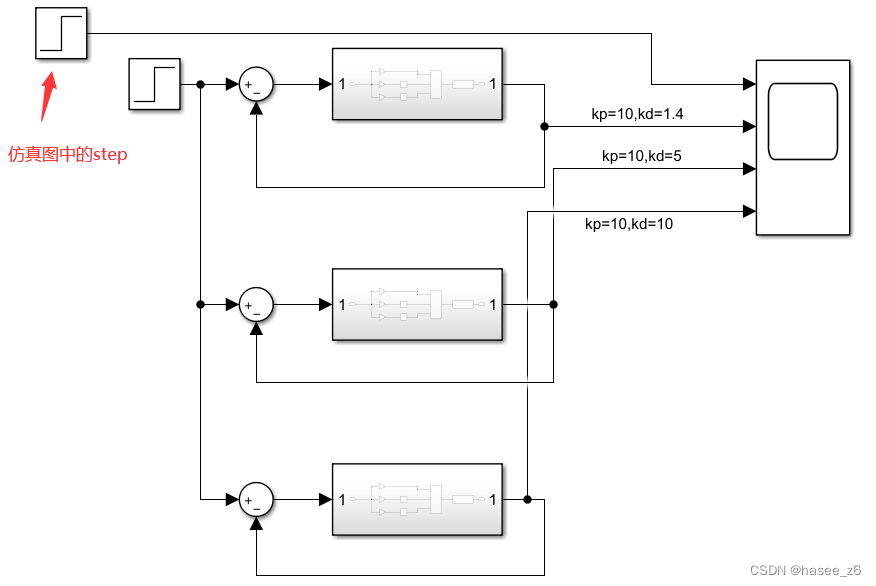
仿真图如下

微分环节的作用能反映偏差信号的变化趋势（变化速率），并能在偏差信号的值变得太大之前，在系统中引入一个有效的早期修正信号，从而加快系统的动作速度，减小调节时间。

可以从图中看出，随着$k_d$增大，曲线调节时间变快，产生的超调减小。

微分环节有助于系统减小超调，克服振荡，减小调节时间，从而改善了系统的动态性能，但微分时间常数过大，会使系统出现不稳定。微分控制作用一个很大的缺陷是容易引入高频噪声，所以在干扰信号比较严重的流量控制系统中不宜引入微分控制作用，或者说使得系统的固有频率增大[9]，固有频率增大会越接近高频噪声的频率，使得整个系统产生共振，而共振会导致机械系统损坏。

参考[3]@李崇的回答，从根轨迹的角度来说，D环节相当于引入了新的零点$(k_p+k_d\cdot s)Gk(s)$，使得系统的极点向左半平面移动，使得稳定裕度更大。有些自身不稳定的系统，只靠PI是不能够变稳定的，需要新的零点把闭环特征根给吸引到左半平面来。
有一个系统开环传函$$Gk=\frac{1}{s^2}$$根轨迹的仿真图如下

可以看出根轨迹在虚轴上，可以知道拥有在虚轴上的特征根的闭环系统响应是等幅震荡的。而我们通常以开环增益$k$作为某一参数，也就是说无论开环增益$k$如何变化，根轨迹始终都在虚轴上，系统响应都是等幅震荡。
我们将零点加上去$$Gk(s)=\frac{s+1}{s^2}$$根轨迹的仿真图如下

从图中可以看出，加入零点后，系统的特征根除了原点外全都往左半平面跑了，而且随着开环增益的增大，系统变得稳定，系统的特征根越远离虚轴。

我们知道伯德图是系统频率响应的一种图示方法，利用伯德图可以看出在不同频率下，系统增益的大小及相位，也可以看出增益大小及相位随频率变化的趋势，还可以对系统稳定性进行判断。$$Gk(s)=s+1$$bode图仿真图如下

可以看出，随着频率增大，系统增益也随之增大，幅值变大，把小的尖刺给放大，这也就是微分会使高频噪声放大。参照[3]，输入信号$$sin(10t)+0.01sin(100t)$$具体看图

算是低频的微分图

高频的微分图

两个函数叠加

从上图看出，随着频率增大，微分后出现尖刺。
可以来个更明显的

从图中就可以看出，当高频噪声的幅值提高十倍的时候，随着频率的增大，微分后出现尖刺更多也更密集。
如此看来，当系统中拥有高频噪声时，使用微分环节会造成系统响应含有更多的尖刺，而不是平滑的图像，造成系统震荡。

(补充:在PID控制中，加入微分项相当于加入了阻尼，使得阻尼比变大，这样可以使震荡快速衰减，变得稳定。)

PID控制

PID控制通过积分作用消除误差，而微分控制可缩小超调量、减少调节时间，是综合了PI控制和PD控制长处并去除其短处的控制。

位置式和增量式

数字 PID 控制算法因时间离散化不同，通常分为位置式 PID 控制算法和增量式 PID 控制算法，具体文章可参考[7]
有几点需要记住：
① 最大超调量是响应曲线的最大峰值与稳态值的差，是评估系统稳定性的一个重要指标；上升时间是指响应曲线从原始工作状态出发，第一次到达输出稳态值所需的时间，是评估系统快速性的一个重要指标；静差是被控量的稳定值与给定值之差，一般用于衡量系统的准确性。
② 关于积分积累误差，可以想象成用高度1米水缸接水。比如期望是接满1米，水龙头开始放水，放到水缸80厘米，然后把水龙头关掉，水缸里的水高度和期望相差20厘米，即使没有了输入，误差也会保持不变，这就是积分作用，水缸本身就是个积分结构，能把水一直储存下来。而如果是直流电机，一旦没有了输入，那么误差就会变成期望减去零，因为它本身没有积分结构，这时就需要积分作用来在它误差为零时，保持它的转速稳定在期望值。更多详细可以参考文章[5][6]
③饱和是执行机构的一个特性，定义为：一开始因变量会随着自变量的增大而增大，而当自变量到达某个特定范围时，因变量将不再随着自变量的增大而有明显的改变，而是不断逼近或停止在某个最大值附近。我的理解是开门只能开180°，但是你非要开360°，那肯定是不行的，因为门已经被墙卡住了。但是因为有积分环节，它会一直累积误差，输出360°，但是门却被墙卡住了，转不到360°。然后你又想关门，这时系统会从360°开始减小角度，实际门却没有动，等到输出小于180°的时候门才会有动作，你会觉得这个反应不是很灵敏，这是因为有一段时间是等待系统从积分饱和出来，减到180°，门才会有动作。

参考文章
[1] 深入浅出PID控制算法
[2] PID
[3] PID 的微分环节主要作用是什么
[4] PID中Kp，Ki，Kd跟Kp，Ti，Ti之间的关系式
[5] pid控制器输出的量到底是什么
[6] 如何通俗地解释 PID 参数整定
[7] 位置式与增量式PID
[8] 积分饱和
[9]九、控制与pid
[10]关于固有频率及阻尼