二叉树，B-Tree，B+Tree详细理解

二叉树介绍：

二叉树的特性：

      1.树的每个节点最多只能有两个子节点，称为左子树与右子树

      2.左子树上所有结点的值均小于或等于它的根结点的值。

      3.右子树上所有结点的值均大于或等于它的根结点的值。

      4.左、右子树也分别为二叉排序树。

      叶子节点的定义:如果一个节点既没有左孩子，也没有右孩子，则该节点为叶子节点。

来陪我看一颗典型的二叉树：

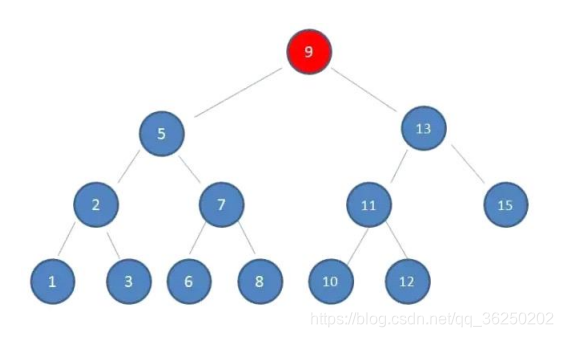
例如用这棵树找10的一个过程：

1.查看根节点9：

2.由于10 > 9，因此查看右孩子13：

3.由于10 < 13，因此查看左孩子11：

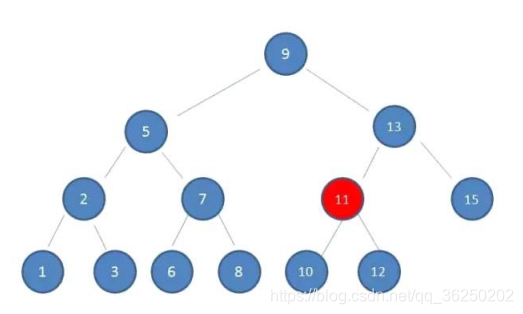
4.由于10 < 11，因此查看左孩子10，发现10正是要查找的节点：

这种方式正式二分查找的思想，查找所需的最大次数等同于二叉查找树的高度 在插入节点的时候也是利用类似的方法，通过一层一层比较大小，找到新节点适合插入的位 置。

查找总结：查找次数=树的深度

 

二叉树的缺陷：

假设：初始的二叉查找树只有三个节点，根节点值为9，左孩子值为8，右孩子值为12：

接下来我们依次插入如下五个节点：7,6,5,4,3。依照二叉查找树的特性，结果会变成什么样呢？

可以看到，二叉树变成了瘸子，查找几乎变成了线性查找。

 

 

B-Tree介绍：

B-tree树即B树，B即Balanced，平衡的意思。B-树是一种多路搜索树(并不一定是二叉的)1970年，R.Bayer和E.mccreight提出了一种适用于外查找的树，它是一种平衡的多叉树，称为B树(或B-树、B_树)。数据库的索引一般采用树结构来存储，可以提高查询效率，但为什么不用二叉查找树呢？而一般用B-树或B+树呢？

其实，B-树或B+树类似于二叉查找树，查找次数都是logn，但前者比后者强的地方在于：

①同样的数据，前者的n更小，即树更矮胖。

②前者可以实现自平衡

无论是二叉树还是B树，树结构和磁盘页的关系都可以这样来理解：

树结构：

磁盘页：

所以，如何提升查询效率——>等价于如何减少IO次数——>等价于如何减少树的深度。

B树（B-tree）比二叉树强的地方就在于，同样的数据，B树更矮胖，以及B树可以达到自平衡结构。如下图：

B-树的特点：

B-树（Balance Tree），不要读成 B减树。而是B树

一个m阶的B树具有如下几个特征：

• 树中的每个结点至多有m颗子树。
• 若根结点不是叶子结点，则至少有两颗子树。
• 除根结点外，所有非终端结点至少有[ m/2 ] ( 向上取整 )颗子树,最多m棵。
• 所有的非终端结点中包括如下信息的数据
• 所有的叶子节点都位于同一层

每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

k值定义：

m/2 <= k <= m

例如：通过B-树查找 5 

第1次磁盘IO：

第2次磁盘IO：

第3次磁盘IO：

在内存中定位（和3，5比较）：

通过整个流程我们可以看出，B-树的查询中的比较次数其实不比二叉查找树少，尤其当单一

节点中的元素数量很多时。

B-Tree的插入和删除：

比如向B-树中插入一个4，自顶向下查找4的节点位置，发现4应当插入到节点元素3，5之间。

节点3，5已经是两元素节点，无法再增加。父亲节点 2， 6 也是两元素节点，也无法再增

加。根节点9是单元素节点，可以升级为两元素节点。于是拆分节点3，5与节点2，6，让根节

点9升级为两元素节点4，9。节点6独立为根节点的第二个孩子。

所以B-树始终能维持多路平衡（自平衡）

删除11元素:

删除11后，节点12只有一个孩子，不符合B树规范。因此找出12,13,15三个节点的中位数

13，取代节点12，而节点12自身下移成为第一个孩子。（这个过程称为左旋）

B+Tree介绍：

B+ 树是一种树数据结构，是一个n叉排序树，每个节点通常有多个孩子，一棵B+树包含根节

点、内部节点和叶子节点。根节点可能是一个叶子节点，也可能是一个包含两个或两个以上孩

子节点的节点。

B+ 树通常用于数据库和操作系统的文件系统中。NTFS, ReiserFS, NSS, XFS, JFS, ReFS 和

BFS等文件系统都在使用B+树作为元数据索引。B+ 树的特点是能够保持数据稳定有序，其插

入与修改拥有较稳定的对数时间复杂度。B+ 树元素自底向上插入。

B+树是B-树的一种变体，性能比B-树更好。

B+树除了具有B-树的特征外，也具有一些新的特性

B+Tree的特点 ：

1.有k个子树的中间节点包含有k个元素（B树中是k-1个元素），每个元素不保存数据，只用来索引

2.所有的叶子结点中包含了全部元素的信息，及指向含这些元素记录的指针，且叶子结点本身依关键字的大小自小而大顺序链接。

3.所有的中间节点元素都同时存在于子节点，在子节点元素中是最大（或最小）元素。

上图就是一个B+树，不但节点之间含有重复元素，而且叶子节点还用指针连在一起。这就是 B+树的特点。

首先，每一个父节点的元素都出现在子节点中，是子节点最小（或最大的元素）。

根节点元素8是子节点2,5,8的最大元素，也是叶子节点6,8的最大元素根节点元素15是子节点11,15的最大元素，也是叶子节点13,15的最大元素需要注意的是，根节点的最大元素（15）也是B+树的最大元素，以后无论插入删除多少元素，始终要保持最大元素再根节点中。此外，每个叶节点都带有指向下一个节点的指针，形成了一个有序链表。

B+树的范围查询:

当做范围查询时，B+树的性能要远远高于B-树，比如我们搜索3~11范围的数据，如果是B-树的话：

自顶向下，查找到范围的下限（3）:

中序遍历到元素6：

中序遍历到元素8：

中序遍历到元素9：

中序遍历到元素11，遍历结束：

B-Tree在范围查找时整个过程非常繁琐

采用B+树后，只需要在链表上做遍历即可：

自顶向下，查找到范围的下限（3）：

通过链表指针，遍历到元素6, 8：

通过链表指针，遍历到元素9, 11，遍历结束：

三棵树分享到这里，有源码我会补全。