数值分析北航第八题第三次计算实习任务（附百度云源码java版）

先上干货 ，包含word报告与源码。

链接：https://pan.baidu.com/s/1piPSQIqsBcLH_pHAYog5tw
提取码：55jo

稍加说明，这是java版的源码以及上交作业的完整文档，如果你胆子大，可以直接将其作为作业上交，后果自负。云盘文件如上

 

首先，理清一下思路，相信还是有不少人跟我一样看见题目的第一眼并不理解什么意思，别说用什么算法了，连思路都没有：

题目给出x=0.08i,y=0.5+0.05j,0≤x≤0.8,0.5≤y≤1.5,所以（x,y）有11×21种组合，直接求出来。

第一步，求出11×21组x,y后，将x,y带入方程组中，于是方程组就变成了4元4个方程组，可以求得对应的t,u,w,v。（这里解方程组解的是非线性方程组，一般用牛顿迭代法，且每组x,y解一次方程组，一共解11×21次）也就是说，可以得出一个数表有11×21条数据（x,y,t,u,w,v）

第二步，题目中给出的数表是z,u,t的数表，而要求得是z,x,y相关的数据，需要利用第一步11×21的x,y,t,u对应关系。首先，利用题目中二维数表求得z=g(u,t)，这个g(u,t)是t,u的双二次表达式，这里利用分片双二次插值求出z与u,t的函数关系，再利用第一步中11×21的数据关系，求出当x=0.08i,y=0.5+0.05j时z的数值，即求得11×21组的x,y,f(x,y)数据对应关系。

第三步，利用第二步得到的11×21组x,y,f(x,y)关系，最小二乘法曲面拟合法对其进行拟合，曲面拟合时随着k值得增加，拟合的精度增加，直到达到题目中要求精度，求得此时的系数矩阵，即得出p(x,y)

第四步，求f(x*,y*)和p(x*,y*),这里已不涉及新算法，直接将x*,y*代入方程组求得u,t,根据z=g(u,t)求得对应z，即f(x*,y*),实际上同第二步一样，只是x,y变化了。p(x*,y*)直接根据第三步计算的参数进行计算。

 

书上和百度云的word报告都有具体算法，不再赘述，简单说几个有意思的点吧：

1.牛顿迭代法需要求导，学的时候并没有细想，觉得这个太复杂了，求导每次都不一样，但实际上方程未变，导数形式未变，只是参数变了，是具有通用性的。如sinx求导cosx，x在迭代中或者不同参数计算时，是改变的，但是主体的cos是恒定的，具有通用性的。

2.分片双二次插值法：题目要求二次插值即可，但给出了6×6的数表，这个6×6的数表足以生成5次插值，所以采取分片，分片算法写得有点复杂，但实际非常简单，双二次插值只需3×3的数表，所以分片时即把最近似贴近的3×3。比如t的取值有0,0.2,0.4,0.6,0.8,1.0，如当t=0.3时，就取0,0.2,0.4这三排的其中数据。

3.曲面拟合：计算矩阵时要合理变通。曲面拟合要计算如下矩阵C

为了简化计算和编程、避免矩阵求逆：

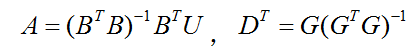
变形得到如下：

这样就变成了求线性方程组，当A是一个矩阵而不是向量，矩阵视为多个向量组成，多次调用列主元guass消去解方程组即可。

 

凡是开源后果自负