机器学习--分类标准

分类准确度

分类准确度是常用的一种评测模型的标准，假设训练出的模型是$f$，测试集是$X$，则分类准确度为
$$\frac{1}{m}\sum _{i=1}^m\mathbb{I}(f(X^{(i)})=y_i)$$
其中$\mathbb{I}$表示指示函数，后面的表达式如果为真那就返回1，否则返回0。
分类准确度表达了对于所有的测试数据模型能够预测正确多少，但是这样的指标有时无法真正地反映出模型的好坏，所以需要另一个指标来进行描述

精确率与召回率(查准率与查全率)

二分类

假设有一个任务是一个二分类，用来预测某些人是否患病，假设这种病患病率只有99.9%，那么此时就会出现问题。
如果模型在预测时，把所有的人都给预测成没病，此时模型的准确度可以达到99.9%但是实际上一个有病的人都没预测出来，这样的模型是没有意义的。

此时就需要一个指标来评估模型在那些需要关注的类别上做出来的效果如何，那么精确率(precision)与召回率(recall)就可以结果这个问题。

首先先把整个测试数据集分成两份，一份是确实生病的记为1，另一份是没病的记为0.
然后对于这样份中，预测正确的再记为1，错误的记为0。那么就得到了这么一个矩阵。

	预测结果	预测结果
实际情况	没病（0）	有病（1）
没病（0）	TN	FP
有病（1）	FN	TP

T表示True，F表示False，如果是T的话表示预测正确，反之预测错误。
而N表示Negative，P表示Positive，如果是P则表示这个例子是想要关注的，也就是正例，反之就是反例。
上面这个矩阵就叫做混淆矩阵。
而精确率的定义是$$\frac{TP}{FP+TP}$$即预测出来为有病的准确率是多少，或者说当预测为有病时那么它的可信度是多少。

而召回率的定义是
$$\frac{TP}{TP+FN}$$
它的含义是在所有有病的病人中，模型找出来了多少。

也就是说准确率可以衡量对于关注的类别，模型预测对时它的可信度有多高。
而对于召回率则是，模型能把多少关注的数据预测出来。

对于上述的那种预测情况假设有1000个人，它的混淆矩阵就是

	预测结果	预测结果
实际情况	没病（0）	有病（1）
没病（0）	999	0
有病（1）	1	0

此时对于精确率来说，分母出现了0这种情况，我们默认此时精确率为0
而对于召回率来说，此时召回率也为0，而对于分类准确率来说却是99.9%

由此可以得出，对于一些类别数量分布严重不均衡的数据集，分类准确率并不能很好的表示模型的实际性能。
在sklearn中可以从metrics中导入confusion_ matrix来获得一个混淆矩阵
可以通过metrics中的precision_score和recall_score来获取精确率和召回率

多分类

sklearn的confusion_matrix同样也以制作多分类的混淆矩阵，与二分类相同，纵轴是表示真实值，横轴表示预测值。
以手写sklearn的手写数字为例，使用LogisticRegression来进行预测。

import numpy as np
import sklearn.datasets
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.metrics import confusion_matrix
from sklearn.metrics import precision_score
digits = sklearn.datasets.load_digits()
data = digits['data']
target = digits['target']

X_train, X_test, y_train, y_test = train_test_split(data, target, train_size=0.7, random_state=666)
log_reg = Pipeline([
    ('std', StandardScaler()),
    ('log_reg', LogisticRegression(penalty='l2', C=5))
])
log_reg.fit(X_train, y_train)
matrix = confusion_matrix(y_test, log_reg.predict(X_test))
print(matrix)
"""
[[57  0  0  0  0  1  0  0  0  0]
 [ 0 47  0  0  0  0  0  0  2  0]
 [ 0  1 51  1  0  0  0  0  0  0]
 [ 0  0  0 55  0  2  0  0  4  0]
 [ 0  3  0  1 52  0  0  0  0  0]
 [ 0  0  0  0  0 50  1  0  1  0]
 [ 0  0  0  0  1  0 46  0  0  0]
 [ 0  0  0  0  0  0  0 51  0  1]
 [ 0  4  0  0  0  0  0  1 51  1]
 [ 1  0  0  1  1  1  0  0  2 49]]
"""

而对于多分类问题则有micro和macro和weight指标可以使用。

macro

对于macro也叫宏观指标，它的做法是每一个种类的Precision或者Recall求出来，然后再求和取平均。
$$Macro-Precision=\frac{1}{m}\sum _{i=1}^{n}Precisio{n}_i$$
$$Macro-Recall=\frac{1}{m}\sum _{i=1}^{n}Recal{l}_i$$
想要求出也不麻烦，对于一个多分类问题，在其对角线上的就是预测正确的，想要求某个类别的Precision只需要用对应的对角线上的值除以这一列的所有值的和就行，Recall也是同样的做法。
同样的也可以指定sklearn求出某个具体类别的Recall或者Precision只需要指定labels参数就可以

matrix = confusion_matrix(y_test, pre)
print(matrix)
print(precision_score(y_test, pre, average='macro',labels=[0]))
"""
[[ 57   0   1]
 [  0  45   4]
 [  3   7 423]]
0.95
"""

micro

micro的做法就不一样了，它是先对每个类别的$TP,TN,FP,FN$求平均，然后再根据Precision和Recall的定义式求
$$Micro-Precision=\frac{T{P}_{mean}}{T{P}_{mean}+F{P}_{mean}}$$
$$Micro-Recall=\frac{T{P}_{mean}}{T{P}_{mean}+F{N}_{mean}}$$

pre = log_reg.predict(X_test)
matrix = confusion_matrix(y_test, pre)
print(matrix)
print(precision_score(y_test, pre, average='micro'))

weight

weight不再像macro一样取平均，而是取得加权平均，权重来自于该类别在传入的标记中的所占的比例
更详细的可以看一下这篇文章
这里

平衡点与F1

通常情况下精准率和召回率是不可兼得的。
通常情况下，想要提高召回率就要增加选中为1的样本数目但同时也会难免选中一些0从而导致精准率下降，反之也是。
如果用横轴表示召回率，纵轴表示精准率，那么大概会得到这么一种曲线。

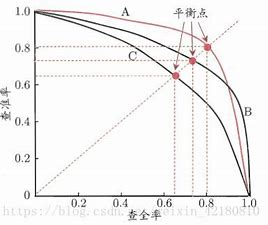
可以看到，随着召回率的提升，精准率也会下降而两个值相等的点就叫做平衡点(break-even-point)。
如果一个模型的曲线能够完全包住领一个模型的曲线，则可以说明被包住的曲线的模型的性能低于包住它的曲线的模型的性能。

平衡点的高低可以反映一个模型在精准率和召回率想当时其模型性能的如何，但是这样还是太粗糙了，所以引入了一个新的评估标准叫做F1量$$\frac{1}{F1}=\frac{1}{2}(\frac{1}{Precision}+\frac{1}{Recall})$$
即F1是精准率与召回率的调和平均数
即$$F1=\frac{2}{(\frac{1}{Precision}+\frac{1}{Recall})}$$
根据均值不等式的性质可以知道当$Precision=Recall$时F1取最大，同时两者的值约到F1也越大，而且对于调和平均数来说它更注重于某个数的最小值。

但是对于不同的任务来说有的任务更倾向于召回率，有的更倾向于精准率，所以需要引入一个权重来对这两个值进行加权。
$$F1=\frac{1+{\beta }^2}{(\frac{1}{Precision}+\frac{{\beta }^2}{Recall})}$$
当$\beta$值越大召回率的权重就越大，因为此时召回率只需要稍微变小一点就会使F1急剧的降低，所以当$\beta$大于1时召回率权重更大，小于1时精准率的权重更大。

有时会多次对模型进行测试，比如交叉验证，此时就会得到多个混淆矩阵，那么此时算F1有两种做法，一是可以把每个矩阵的Precision和Recall都给求出来然后去平均再去求F1，也可以吧每个混淆矩阵进行相加然后取平均再求F1

ROC与AUC

ROC的全称是受试者工作特征( Receiver Operating Characteristic)
它需要计算两个值一个是$$TPR=\frac{TP}{TP+FN}$$
另一个是$$FPR=\frac{FP}{TN+FP}$$
把混淆矩阵拿出来很容易就很容易理解

	预测结果	预测结果
实际情况	没病（0）	有病（1）
没病（0）	TN	FP
有病（1）	FN	TP

很明显，随着TPR的提高，FPR也会随之提高，因为在预测正确的人数提高时也难免会导致预测错误的产生。

以横轴为FPR纵轴为TPR则绘制出来的曲线就是ROC曲线，而ROC曲线与横坐标轴所围成的面积就是AUC，可以很简单的得到$$0<AUC<1$$

使用sklearn的roc_curve就可以绘制出这条曲线

FPR, TPR, th = roc_curve(y_test, pre)
plt.plot(FPR, TPR)
plt.show()

同时也可以使用roc_auc_score来获取AUC的值