国庆清北刷题冲刺班 Day3 下午

最新推荐文章于 2021-03-16 20:24:44 发布

原创最新推荐文章于 2021-03-16 20:24:44 发布 · 366 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#三分答案 #数学 #动态规划 #贪心 #模拟

数学同时被 3 个专栏收录

75 篇文章

订阅专栏

搜索

53 篇文章

订阅专栏

模拟考试

51 篇文章

订阅专栏

本文介绍了使用栈进行括号匹配的实现方法，并探讨了通过三分法优化算法的过程及树形结构中路径转换的策略。

这里写图片描述

//长者的送分题  栈模拟
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<stack>
using namespace std;
stack<char> st;
char s[10005];
int main(int argc,char *argv[]){
    freopen("a.in","r",stdin);
    freopen("a.out","w",stdout);
    scanf("%s",s+1);
    int n=strlen(s+1);
    for(int i=1;i<=n;++i){
        if(s[i]=='('||s[i]=='['||s[i]=='{'){ st.push(s[i]); continue; }

        if(s[i]==')'&&!st.empty()&&st.top()=='('){ st.pop();continue; }
        if(s[i]==')'&&( st.empty()||st.top()!='(' )){ printf("Wrong\n"); return 0; }

        if(s[i]==']'&&!st.empty()&&st.top()=='['){ st.pop();continue; }
        if(s[i]==']'&&(st.empty() ||st.top()!='[' )){ printf("Wrong\n"); return 0; }

        if(s[i]=='}'&&!st.empty()&&st.top()=='{'){ st.pop();continue; }
        if(s[i]=='}'&&( st.empty()||st.top()!='{' )){ printf("Wrong\n"); return 0; }

    }
    if(!st.empty()) printf("Wrong\n");
    else printf("OK\n");
    fclose(stdin);fclose(stdout);
    return 0;
}

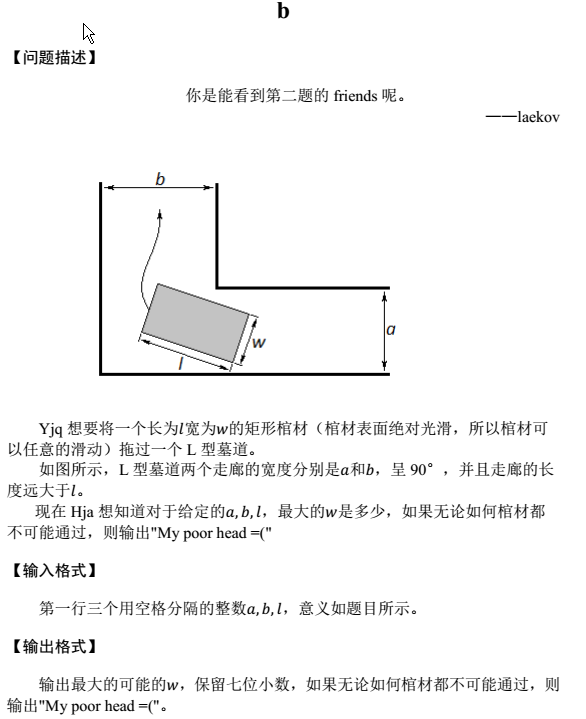
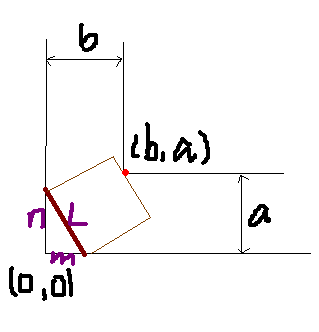
这里写图片描述

设直线解析式为 y=（-n/m）* x+n
整理，得：- n * x + m * y + n * m = 0
点（b，a）到直线的距离为：| - b * n - a * m + n * m | / L
(L : 根号下（n^2 + m^2）=L)
最优解就是 - b * n - a * m + n * m 的最大值
然后不知道为啥求了个
b * n + a * m - n *m 的最小值
单峰函数求最小值，三分法每次去掉大的一部分
式子最小值<0 时无解

//三分答案
#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
const double eps = 1e-9;
int a,b,l;
double f (double n){
    double m = sqrt(1.0 * l * l - n * n);
    if(n * m > a * n + b * m) return -1;
    return (b * m + a * n - n * m) / l;
}

int main(int argc,char *argv[]){
    freopen("b.in","r",stdin);
    freopen("b.out","w",stdout);
    scanf("%d%d%d", &a, &b, &l);
    if(a >= l && b >= l){ printf("%d.0000000", l); return 0; }
    if(a >= l){ printf("%d.0000000\n",b); return 0; }
    if(b >= l){ printf("%d.0000000\n",a); return 0; }
    double L = 0, R = l,Ans = 1e9,Mid1,Mid2,t1,t2;
    int T = 100;
    while(T--){
        Mid1 = (R - L)/3.0 + L,Mid2 = L + R -Mid1;
        t1 = f(Mid1),t2 = f(Mid2);
        if(t1 < 0 || t2 < 0){ printf("My poor head =("); return 0; }
        if(t1 < t2) Ans = min(Ans,t1),R=Mid2;
        else Ans = min(Ans ,t2), L = Mid1;
    }
    printf("%.7lf\n",Ans);
    fclose(stdin);fclose(stdout);
    return 0;
}

这里写图片描述

变成环，一定是变成一条链，然后加一条边变成环。
那么怎么变成链呢?
考虑整棵树的根节点，假设子树已经变成链了，子树的链有两种可能：顶底是链端、顶点不是链端。如果不是链端，一定要出来,如果是链端，可以不去掉。
第二维标记,0代表任意情况，只要变成链就可以。1代表要求顶点必须为链端。每一层横向递推即可。
【分析来自张家和的个人主页】

#include<iostream>
#include<vector>
#include<cstring>
#include<cstdio>
#include<algorithm>

using namespace std;
#define INF 0x3f3f3f3f
#define MAXN 100010
struct Edge{ int to,next; }e[MAXN<<1];
int head[MAXN],f[MAXN][2],tot;

inline void read(int &x){
    x=0; int f=1; char c=getchar();
    while(c>'9'||c<'0'){ if(c=='-')f=-1; c=getchar(); }
    while(c>='0'&&c<='9'){ x=x*10+c-'0'; c=getchar(); } x*=f;
}

inline void Add_Edge(int u,int v){
    e[++tot].to = v, e[tot].next = head[u], head[u] = tot;
    e[++tot].to = u, e[tot].next = head[v], head[v] = tot;
}

void DFS(int u,int root){
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v != root) DFS(v, u);
    }
    int flag = 0,cnt = 0,sum = 0,n0 = 0 ,n1 = INF ,n2 = INF;
    for(int i = head[u]; i; i = e[i].next){
        int v = e[i].to;
        if(v != root){
            flag = 1;
            n2 = min(n2 + f[v][0] + 2,n1 + f[v][1]);
            if(n2 > INF) n2 = INF;
            n1 = min(n1 + f[v][0] + 2,f[v][1] + cnt * 2 + sum);
            ++cnt;
            sum += f[v][0];
        }
    }
    if(flag == 0){ f[u][0] = f[u][1] = 0; return ; }// Leaf Node
    f[u][0] = min(n1, n2);
    f[u][1] = n1;
}

int main(int argc,char *argv[]){
    freopen("c.in","r",stdin);
    freopen("c.out","w",stdout);
    int n,u,v;
    read(n);
    for(int i=1; i<=n-1; ++i){
        read(u),read(v);
        Add_Edge(u,v);
    }
    DFS(1,0);
    printf("%d\n",f[1][0]+1);
    fclose(stdin);fclose(stdout);
    return 0;
}