算法的概念:
- 空间复杂度:一句来理解就是,此算法在规模为n的情况下额外消耗的储存空间。
- 时间复杂度:一句来理解就是,此算法在规模为n的情况下,一个算法中的语句执行次数称为语句频度或时间频度。
- 稳定性:主要是来描述算法,每次执行完,得到的结果都是一样的,但是可以不同的顺序输入,可能消耗的时间复杂度和空间复杂度不一样。
一、二分查找算法
二分查找又称折半查找,优点是比较次数少,查找速度快,平均性能好,占用系统内存较少;其缺点是要求待查表为有序表,且插入删除困难。这个是基础,最简单的查找算法了。
public static void main(String[] args) {
int srcArray[] = {3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
System.out.println(binSearch(srcArray, 28));
}
/**
* 二分查找普通循环实现
*
* @param srcArray 有序数组
* @param key 查找元素
* @return
*/
public static int binSearch(int srcArray[], int key) {
int mid = srcArray.length / 2;
// System.out.println("=:"+mid);
if (key == srcArray[mid]) {
return mid;
}
//二分核心逻辑
int start = 0;
int end = srcArray.length - 1;
while (start <= end) {
// System.out.println(start+"="+end);
mid = (end - start) / 2 + start;
if (key < srcArray[mid]) {
end = mid - 1;
} else if (key > srcArray[mid]) {
start = mid + 1;
} else {
return mid;
}
}
return -1;
}
二分查找算法如果没有用到递归方法的话,只会影响CPU。对内存模型来说影响不大。时间复杂度log2n,2的开方。空间复杂度是2。一定要牢记这个算法。应用的地方也是非常广泛,平衡树里面大量采用。
二、递归算法
递归简单理解就是方法自身调用自身。
public static void main(String[] args) {
int srcArray[] = {3,5,11,17,21,23,28,30,32,50,64,78,81,95,101};
System.out.println(binSearch(srcArray, 0,15,28));
}
/**
* 二分查找递归实现
*
* @param srcArray 有序数组
* @param start 数组低地址下标
* @param end 数组高地址下标
* @param key 查找元素
* @return 查找元素不存在返回-1
*/
public static int binSearch(int srcArray[], int start, int end, int key) {
int mid = (end - start) / 2 + start;
if (srcArray[mid] == key) {
return mid;
}
if (start >= end) {
return -1;
} else if (key > srcArray[mid]) {
return binSearch(srcArray, mid + 1, end, key);
} else if (key < srcArray[mid]) {
return binSearch(srcArray, start, mid - 1, key);
}
return -1;
}
递归几乎会经常用到,需要注意的一点是:递归不光影响的CPU。JVM里面的线程栈空间也会变大。所以当递归的调用链长的时候需要-Xss设置线程栈的大小。
三、八大排序算法 (个人理解备注)
- 一、直接插入排序(Insertion Sort)
- 每次向一个有序集合插入一个数据。
- 由后向前遍历,每次如果插入数据大于该数,,这个数据与后面的位置交换
- 当前位置数据小于插入数据,把该数据直接放在当前位置的后一位
- 适合小规模数据
- 二、希尔排序(Shell Sort)
- 指定一个变量,比如10,把集合内间隔10个位置的数放在一组,然后插入排序
- 10/2 =5 把间隔5个单位的数据分在一组,插入排序,如此类推,直到变量变成1
- 适合中小规模数据 (它先划分范围,把排序的范围缩小,对于有序的集合,插入排序会很快)
- 三、选择排序(Selection Sort)
- 找出最大值或最小值
- 每次把最大值放在最后(或最小值放最前面)。
- 优化:每次找出2个值,最大和最小,同时把最大放后面,最小放前面
- 四、堆排序(Heap Sort)
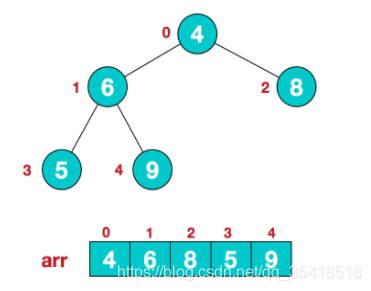
- 把数据看成一颗完全二叉树,用数组下标表示。
- 小根堆(父节点小于子节点),大根堆(父节点小于子节点)。
- 从下至上,把二叉树转成小根堆,或获取最上面的根节点,放在数组最后。
- 一直转换获取根节点,直到所有点找完。
- 一旦发生过节点交换的,下一次转换得重新算一遍。
- 五、冒泡排序(Bubble Sort)
- 通过n-1次遍历,每次遍历找到最大的值,放在当前遍历长度的最后面
- 六、快速排序(Quick Sort)
- 先从数列中取出一个数作为基准数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
- 七、归并排序(Merging Sort)
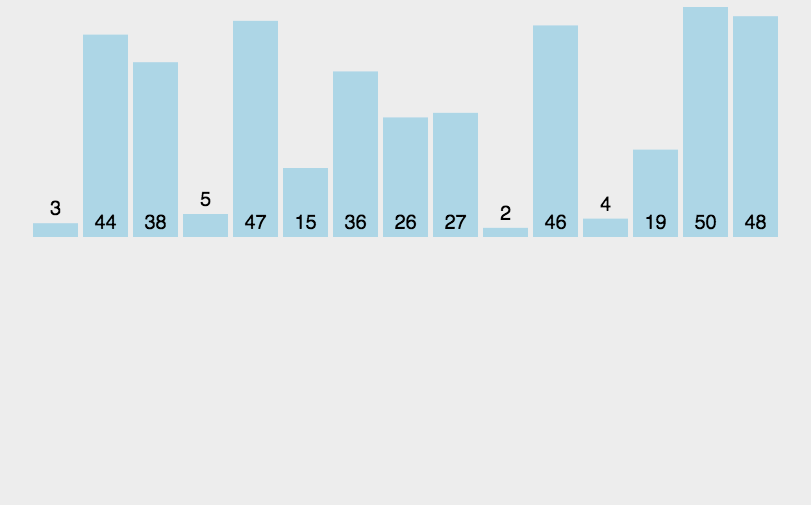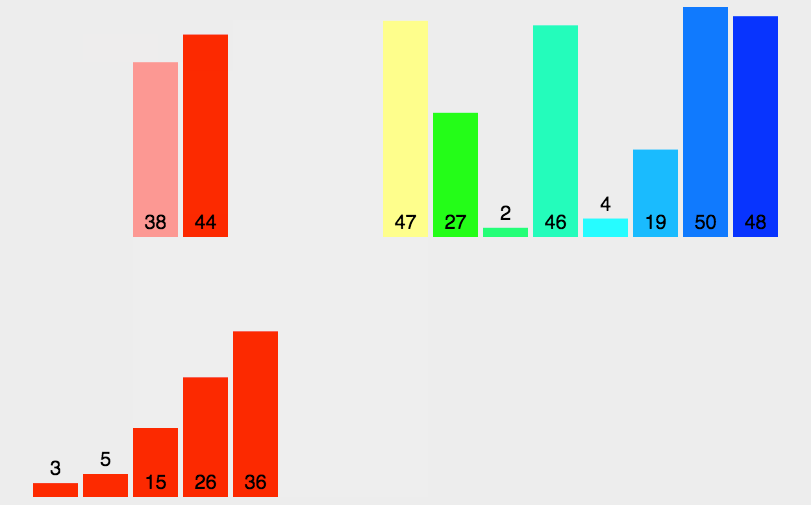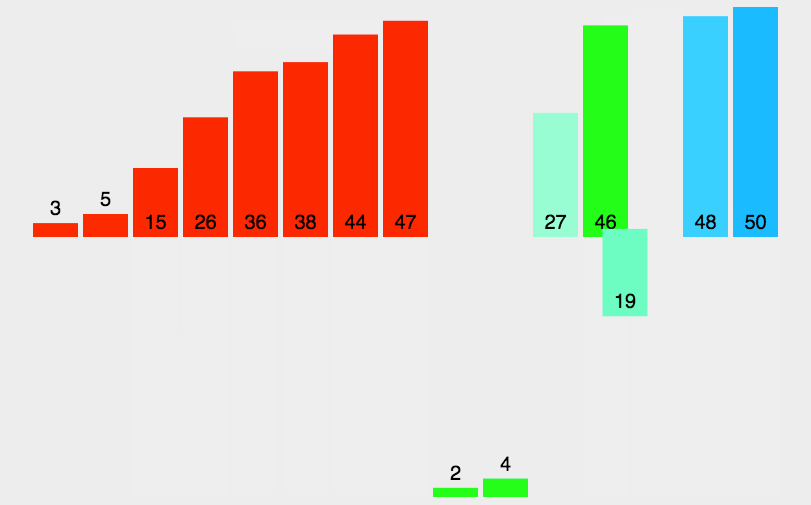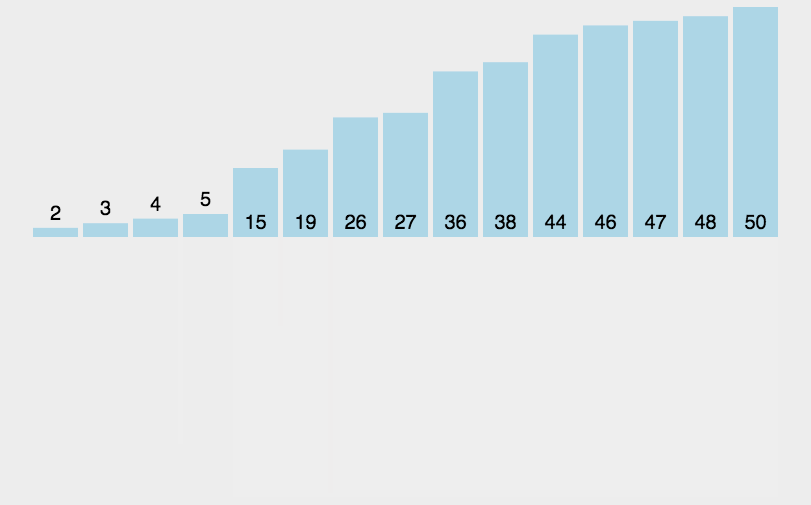
- 每次把数组分成平均的2半,对两半在重复分,直到数据只有1个分不了
- 对分好后的数据排序,然后在对比排序好的数据继续排序
public static void merge(int[] arr, int L, int mid, int R) {
int[] temp = new int[R - L + 1];
int i = 0;
int p1 = L;
int p2 = mid + 1;
// 比较左右两部分的元素,哪个小,把那个元素填入temp中
while(p1 <= mid && p2 <= R) {
temp[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
}
// 上面的循环退出后,把剩余的元素依次填入到temp中
// 以下两个while只有一个会执行
while(p1 <= mid) {
temp[i++] = arr[p1++];
}
while(p2 <= R) {
temp[i++] = arr[p2++];
}
// 把最终的排序的结果复制给原数组
for(i = 0; i < temp.length; i++) {
arr[L + i] = temp[i];
}
}- 八、基数排序(Radix Sort)
- 把数据按照位数排序(个、十、百、千、万、十万)
- 第一次比较个位,个位越小越前面,后面依次十位,百位等
八大算法,网上的资料就比较多了。
吐血推荐参考资料:git hub 八大排序算法详解。此大神比作者讲解的还详细,作者就不在这里,描述重复的东西了,作者带领大家把重点的两个强调一下,此两个是必须要掌握的。
1:冒泡排序
基本思想:
冒泡排序(Bubble Sort)是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
以下是冒泡排序算法复杂度:
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(n²) | O(n) | O(n²) | O(1) |
冒泡排序是最容易实现的排序, 最坏的情况是每次都需要交换, 共需遍历并交换将近n²/2次, 时间复杂度为O(n²). 最佳的情况是内循环遍历一次后发现排序是对的, 因此退出循环, 时间复杂度为O(n). 平均来讲, 时间复杂度为O(n²). 由于冒泡排序中只有缓存的temp变量需要内存空间, 因此空间复杂度为常量O(1).
Tips: 由于冒泡排序只在相邻元素大小不符合要求时才调换他们的位置, 它并不改变相同元素之间的相对顺序, 因此它是稳定的排序算法.
/**
* 冒泡排序
*
* ①. 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
* ②. 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。这步做完后,最后的元素会是最大的数。
* ③. 针对所有的元素重复以上的步骤,除了最后一个。
* ④. 持续每次对越来越少的元素重复上面的步骤①~③,直到没有任何一对数字需要比较。
* @param arr 待排序数组
*/
public static void bubbleSort(int[] arr){
for (int i = arr.length; i > 0; i--) { //外层循环移动游标
for(int j = 0; j < i && (j+1) < i; j++){ //内层循环遍历游标及之后(或之前)的元素
if(arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
System.out.println("Sorting: " + Arrays.toString(arr));
}
}
}
}
2:快速排序
快速排序使用分治策略来把一个序列(list)分为两个子序列(sub-lists)。步骤为:
①. 从数列中挑出一个元素,称为”基准”(pivot)。
②. 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
③. 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
递归到最底部时,数列的大小是零或一,也就是已经排序好了。这个算法一定会结束,因为在每次的迭代(iteration)中,它至少会把一个元素摆到它最后的位置去。
代码实现:
用伪代码描述如下:
①. i = L; j = R; 将基准数挖出形成第一个坑a[i]。
②.j--,由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中。
③.i++,由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中。
④.再重复执行②,③二步,直到i==j,将基准数填入a[i]中。
快速排序采用“分而治之、各个击破”的观念,此为原地(In-place)分区版本。
/**
* 快速排序(递归)
*
* ①. 从数列中挑出一个元素,称为"基准"(pivot)。
* ②. 重新排序数列,所有比基准值小的元素摆放在基准前面,所有比基准值大的元素摆在基准后面(相同的数可以到任一边)。在这个分区结束之后,该基准就处于数列的中间位置。这个称为分区(partition)操作。
* ③. 递归地(recursively)把小于基准值元素的子数列和大于基准值元素的子数列排序。
* @param arr 待排序数组
* @param low 左边界
* @param high 右边界
*/
public static void quickSort(int[] arr, int low, int high){
if(arr.length <= 0) return;
if(low >= high) return;
int left = low;
int right = high;
int temp = arr[left]; //挖坑1:保存基准的值
while (left < right){
while(left < right && arr[right] >= temp){ //坑2:从后向前找到比基准小的元素,插入到基准位置坑1中
right--;
}
arr[left] = arr[right];
while(left < right && arr[left] <= temp){ //坑3:从前往后找到比基准大的元素,放到刚才挖的坑2中
left++;
}
arr[right] = arr[left];
}
arr[left] = temp; //基准值填补到坑3中,准备分治递归快排
System.out.println("Sorting: " + Arrays.toString(arr));
quickSort(arr, low, left-1);
quickSort(arr, left+1, high);
}
以下是快速排序算法复杂度:
| 平均时间复杂度 | 最好情况 | 最坏情况 | 空间复杂度 |
|---|---|---|---|
| O(nlog₂n) | O(nlog₂n) | O(n²) | O(1)(原地分区递归版) |
快速排序排序效率非常高。 虽然它运行最糟糕时将达到O(n²)的时间复杂度, 但通常平均来看, 它的时间复杂为O(nlogn), 比同样为O(nlogn)时间复杂度的归并排序还要快. 快速排序似乎更偏爱乱序的数列, 越是乱序的数列, 它相比其他排序而言, 相对效率更高.
























 2628
2628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








