机器学习课程笔记（第八周-2）降维问题 主成分分析法PCA

课程链接https://www.coursera.org/learn/machine-learning
部分内容整理摘自https://www.cnblogs.com/maxiaodoubao/p/10217672.html

维数约简dimensionality reduction

原因：
1.数据压缩 Data Compression
数据压缩不仅通过压缩数据使得数据，占用更少的计算机内存和硬盘空间，它还能给算法提速
将数据从三维降至二维: 将三维向量投射到一个二维的平面上，强迫使得所有的数据都在同一个平面上，降至二维的特征向量。
2.数据可视化 Data Visualization
降维可以帮助我们将高维数据可视化。

降维问题算法

主成分分析法 Principal Component Analysis（PCA）
寻找到一个低维的平面，对数据进行投影，以便最小化投影误差的平方，即最小化每个点与投影后的对应点之间的距离的平方值。

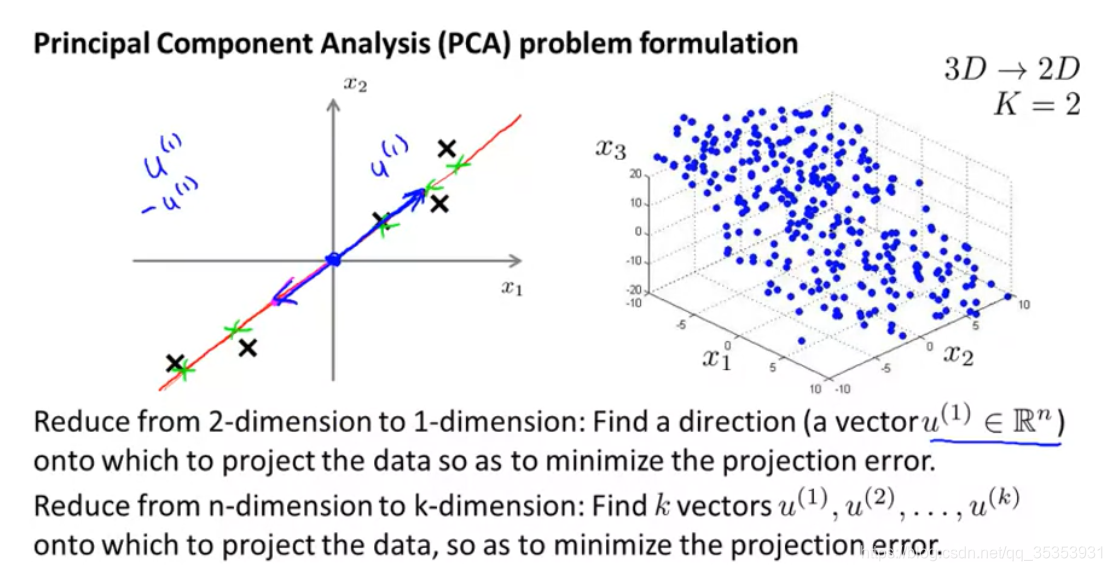
算法描述：
1. 先进行数据预处理。
拿到某组有 m 个无标签样本的训练集，一般先进行均值归一化 (mean normalization) ，还可以进行