51-52. N-Queens I & II [Hard] 回溯

最新推荐文章于 2023-02-14 09:59:10 发布

木木歹朱

最新推荐文章于 2023-02-14 09:59:10 发布

阅读量108

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_35319215/article/details/96921156

本文详细解析了N皇后问题的求解策略，利用深度优先搜索（DFS）算法，通过三个标志数组跟踪列和对角线的状态，确保皇后放置不冲突。提供了两个Python实现：一个是返回所有可能的棋盘布局，另一个只计算解决方案的数量。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

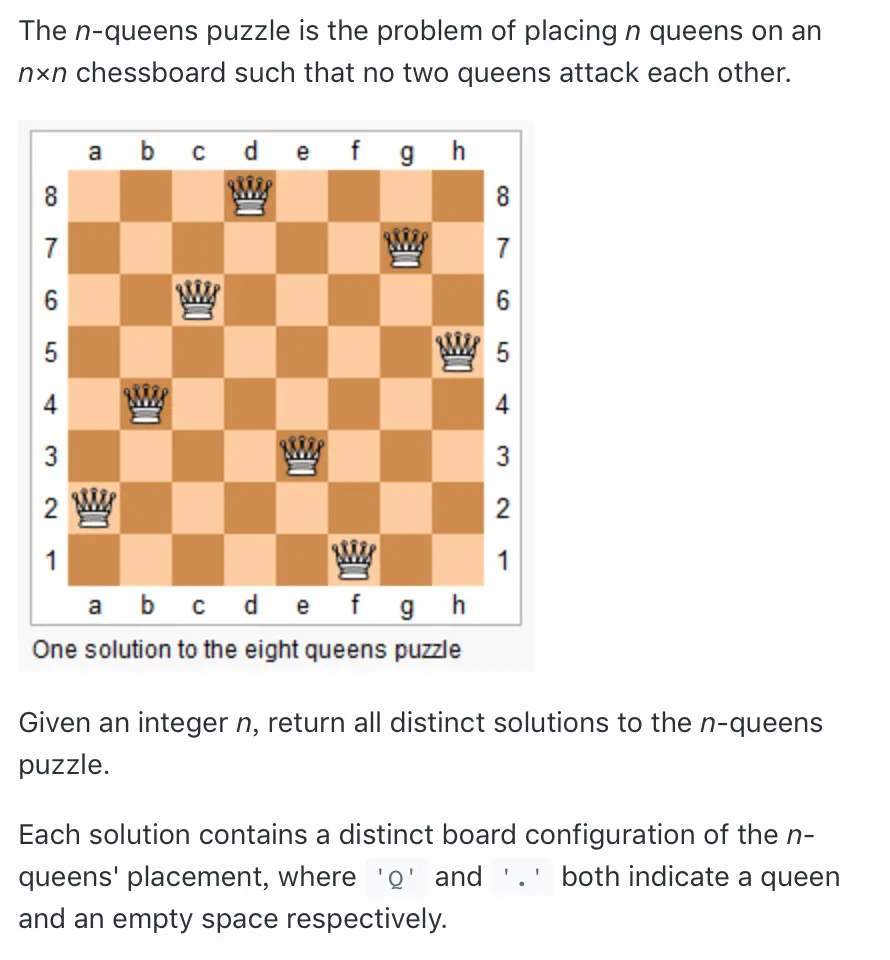
51. N-Queens

把n个皇后放入n*n的网格中，每行，每列，对角都不能相邻。用3个数组记录，每次检查是否在集合中。
可以从每行入手，如果行数到n就加入res
每行从1-n开始检测，如果当前位置可以就继续下一行，如果都不可以就要回溯。

代码如下：

class Solution(object):
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        trace = []
        res = []
        flag_col = [False for i in range(n)]
        flag_45 = [False for i in range(2*n-1)]
        flag_135 = [False for i in range(2*n-1)]
        self.DFS(n, 0, trace, res, flag_col, flag_45, flag_135)
        return res
    def DFS(self, n, k, trace, res, flag_col, flag_45, flag_135):
        if k == n:
            res.append(trace[:])
            return 
        for i in range(n):
            if not flag_col[i] and not flag_45[n-1+k-i] and not flag_135[k+i]:
                temp = '.' * i + 'Q' + '.' * (n - i - 1)
                flag_col[i] = True
                flag_45[n - 1 + k - i] = True
                flag_135[k + i] = True
                trace.append(temp)
                self.DFS(n, k+1, trace, res, flag_col, flag_45, flag_135)
                trace.pop()
                flag_col[i] = False
                flag_45[n - 1 + k - i] = False
                flag_135[k + i] = False

52. N-Queens II

和上题一样了啦，明天再写一遍，看能一次AC不～

代码如下：

class Solution(object):
    def totalNQueens(self, n):
        """
        :type n: int
        :rtype: int
        """
        self.res = 0
        flag_col = [False] * n
        flag_45 = [False] * (2*n-1)
        flag_135 = [False] * (2*n-1)
        trace = []
        self.DFS(n, trace, flag_col, flag_45, flag_135, 0)
        return self.res
    def DFS(self, n, trace, flag_col, flag_45, flag_135, k):
        if k == n:
            self.res += 1
            return
        for i in range(n):
            if flag_col[i]==False and flag_45[i+k]==False and flag_135[n-1+i-k]==False:
                temp = '.' * i + 'Q' + '.' * (n - 1 - i)
                trace.append(temp)
                flag_col[i] = True
                flag_45[i+k] = True
                flag_135[n-1+i-k] = True
                self.DFS(n, trace, flag_col, flag_45, flag_135, k+1)
                trace.pop()
                flag_col[i] = False
                flag_45[i+k] = False
                flag_135[n-1+i-k] = False