R语言笔记⑧——数据挖掘算法

数据挖掘算法

聚类算法

俗话说“物以类聚，人以群分”，在自然科学和社会科学中，存在着大量的分类问题。所谓类，通俗地说，就是指相似元素的集合。

Kmeans算法

K均值法先指定聚类数，目标是使每个数据到数据点所属聚类中心的总距离变异平方和最小，规定聚类中心时则是以该类数据点的平均值作为聚类中心。

对于有N个数据的数据集，我们想把它们聚成K类，开始需要指定K个聚类中心，假设第i类有n个样本数据，计算每个数据点分别到聚类中心的距离平方和，距离这里直接用的欧拉距离，还可以使用海明距离、街道距离、余弦相似度什么的都可以，这里聚类的话，欧式距离就好。

K均值的基本计算公式如下：

• 假设聚类成k类，那么：
  $$\sum _{i=1}^k{n}_i=N$$
• 第i类中数据点到聚类中心距离平方总和di为：
  $$d_i=\sum _{j=1}^{n_i}(x_{ij}-x_i{)}^2$$
• 距离和为：
  $$D=\sum _{i=1}^k{d}_i$$

下面K均值算法的一般步骤：

1. 随机选取K个数据点作为（起点）聚类中心；
2. 按照距离最近原则分配数据点到对应类；
3. 计算每类的数据点平均值（新的聚类中心）；
4. 计算数据点到聚类中心总距离；
5. 如果与上一次相比总距离下降，聚类中心替换；
6. 直到总距离不再下降或者达到指定计算次数。

在R语言中也存在聚类的函数，函数名就是kmeans，通过这个函数我们可以很简单实现数据的聚类分析。

下面就是一个聚类的示例，随机生成40个点，每个点都是2维的，最后需要聚成4类，并画出聚类后的散点图。

> dat <- matrix(runif(80,0,5),2,40)
> dat
          [,1]     [,2]      [,3]        [,4]      [,5]     [,6]     [,7]     [,8]      [,9]     [,10]    [,11]
[1,] 1.8437859 4.897437 0.0639441 0.002375384 4.8200464 3.632813 2.969132 2.176099 0.3277066 2.4966379 3.349614
[2,] 0.8806481 1.421037 1.2393843 4.511674085 0.9533752 2.661892 3.525069 3.179743 3.1598494 0.5983467 3.384036
        [,12]    [,13]    [,14]     [,15]     [,16]    [,17]    [,18]    [,19]    [,20]    [,21]     [,22]    [,23]
[1,] 1.615559 4.147293 1.686646 3.6117509 0.8951700 2.407765 2.488271 4.538294 3.778364 4.157232 1.2781424 3.040823
[2,] 4.134440 3.996854 2.424089 0.6967045 0.7962644 3.407759 4.029680 4.003206 2.327437 4.458846 0.2118136 2.036739
        [,24]     [,25]    [,26]    [,27]    [,28]    [,29]    [,30]     [,31]    [,32]    [,33]     [,34]    [,35]
[1,] 2.706035 0.3152699 3.291890 2.525655 1.350249 3.965873 1.613216 0.5115312 3.503739 4.318836 0.6466194 1.490317
[2,] 4.643759 1.8957941 4.688184 2.667802 2.125648 3.195880 3.983187 2.6419948 1.134634 4.435917 0.2650576 4.225641
        [,36]    [,37]     [,38]    [,39]     [,40]
[1,] 3.856378 3.610459 0.4371379 2.043180 1.6679202
[2,] 4.751183 1.539018 2.2263157 2.431323 0.7244898
> dat <- t(dat)
> kc <- kmeans(dat,4)
> summary(kc)
             Length Class  Mode   
cluster      40     -none- numeric
centers       8     -none- numeric
totss         1     -none- numeric
withinss      4     -none- numeric
tot.withinss  1     -none- numeric
betweenss     1     -none- numeric
size          4     -none- numeric
iter          1     -none- numeric
ifault        1     -none- numeric
> kc$centers
      [,1]     [,2]
1 3.730058 4.108293
2 1.099488 1.096376
3 1.574027 3.399765
4 3.861929 1.596355
> library(ggplot2)
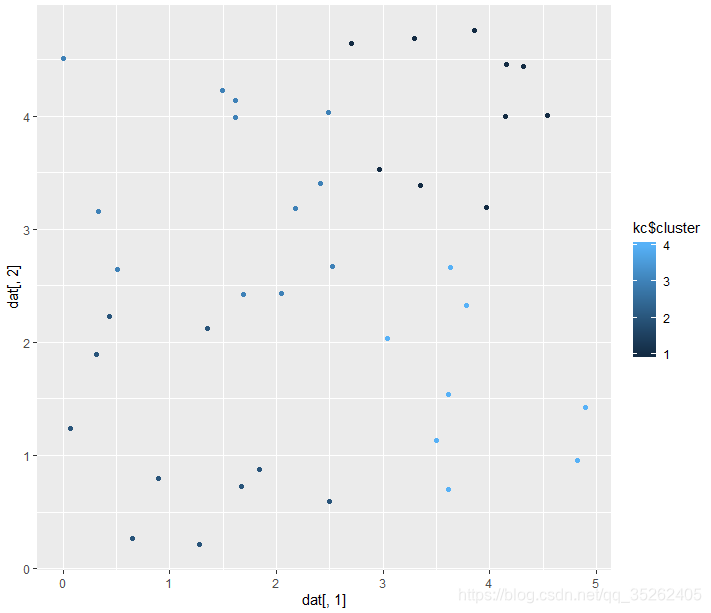
> qplot(dat[,1],dat[,2],colour = kc$cluster)

生成的聚类图如下

协同过滤算法

协同过滤简单来说是利用某兴趣相投、拥有共同经验的群体的喜好来推荐用户感兴趣的信息。

最著名的电子商务推荐系统应属亚马逊网络书店，顾客选择一本自己感兴趣的书籍，马上会在底下看到一行“Customer Who Bought This Item Also Bought”，亚马逊是在“对同样一本书有兴趣的读者们兴趣在某种程度上相近”的假设前提下提供这样的推荐，此举也成为亚马逊网络书店为人所津津乐道的一项服务，各网络书店也跟进做这样的推荐服务如台湾的博客来网络书店。

另外一个著名的例子是Facebook的广告，系统根据个人资料、周遭朋友感兴趣的广告等等对个人提供广告推销，也是一项协同过滤重要的里程碑，和前二者Tapestry、GroupLens不同的是在这里虽然商业气息浓厚同时还是带给使用者很大的方便。以上为三项协同过滤发展上重要的里程碑，从早期单一系统内的邮件、文件过滤，到跨系统的新闻、电影、音乐过滤，乃至于今日横行互联网的电子商务，虽然目的不太相同，但带给使用者的方便是大家都不能否定的。

下面通过一个例子来说明协同过滤算法：

假设存在三样物品和三位用户，我们知道用户对于部分物品的评价，我们需要通过这些评价来评测这些物品之间的相似性，基于物品之间的相似性做出推荐。

物品和用户的关系的描述如下：

物品/用户	用户A	用户B	用户C
物品A	TRUE		TRUE
物品B	TRUE	TRUE	TRUE
物品C	TRUE

物品A与物品B都被用户A和用户C所喜爱，将物品相对于用户表示为向量A（1，0，1），B（1，1，1），C（1，0，0），可以用余弦相似度或者欧式距离来度量，我们更有理由认为物品A与B更相像，我们就把A没有入选而与A更相似的B入选了的用户B推荐给物品A。

物品/用户	用户A	用户B	用户C
物品A	TRUE	推荐	TRUE
物品B	TRUE	TRUE	TRUE
物品C	TRUE

用户与物品时相对的，我们可以等价看待，既可以把物品推荐给可能喜欢的用户，也可以把用户推荐给他可能喜欢的物品。

决策树算法

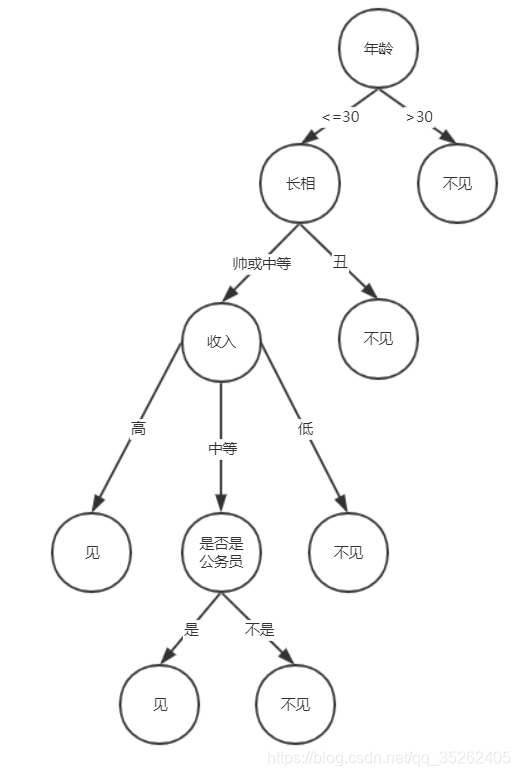
在我们平常生活中都有这样的If-Then的决策过程，我们需要根据不同的环境、情况变量做出最佳的决策，决策变量一般有多个，这里有一个决策树例子，关于一个比较现实的女孩详情问题。

构建决策树的目的

• 探索
• 预测

构建决策树的步骤

1. 数据准备
2. 决策树生长
3. 决策树修剪
4. 规则提取

• 数据准备

决策树的分析数据包括我们需要决策的目标变量与根据问题所选择的可以对目标变量进行决策的分支变量，我们希望分支变量容易理解与解释决策树。

有的属性取值只有二元，比如性别只能取值男女，一道题目的对错。还可以是多个属性值，比如一些学生的年级。还有些属性具有顺序，比如青年、中年、老年，我们不能将它们随意组合。

还有一种属性取值是连续的，我们可以将其表示为比如（X>a）或（X<=a）的形式，将其离散化。比如我们可以吧年龄分成[0，18]，[19，28]，[29，38]等，而不是把每一岁作为一个属性值，就显得非常臃肿与不必要了。

• 训练集与测试集

拿到一份数据，我们需要将其分为训练集合与测试集，比例一般7：3开都可以。训练集用来训练模型，这里就是构建决策树；测试集用来做测试，根据训练的模型来作预测，进而评价模型的好坏。如果发现模型不很好，就需要适当修剪决策树。

• 决策树的分支准则

决策树的分支准则可以决定决策树的大小，包括树的宽度与深度。信息增益、信息增益比、Gini系数。

对于任意属性A，它可能有多个属性值比如颜色这个属性，就有比如红色、蓝色等属性值。我们可以抽象描述任一属性与目标变量类别关系表如下：

A属性值\类别	C1	C2	…	Cn	总和
A1	x11	x12	…	x1n	x1.
A2	x21	x22	…	x2n	x2.
…	…	…	…	…	…
Am	xm1	xm2	…	xmn	xm.
总和	x.1	x.2	…	x.n	N

这里属性A有m各属性值，整个数据共有n个类别，N为所有数据记录数，Xij表示属性值为Ai、类别为Cj的样本数，X.j表示第Cj类的样本数，同理Xi.表示属性值为Ai的样本总数，第j类出现的概率为Pj=X.j/N。

• 信息增益

样本集合C的信息熵为：
$$info(C)=-\sum _{j=1}^n{p}_j{\log }_2{p}_j$$
对于任一属性A，有m个属性值，则用属性A对样本进行划分获得的信息熵为：
$$inf{o}_A(C)=\sum _{i=1}^m\frac{|A_i|}{|A|}info(A_i)$$
最终的信息增益为：
$$Gain(C,A)=info(C)-inf{o}_A(C)$$

• 信息增益比

信息增益最大对应的属性就是需要选择的该节点属性
$$Gain\_ratio(C,A)=\frac{Gain(C,A)}{info(A)}$$
$$info(A)=-\sum _{i=1}^m\frac{|A_k|}{|A|}{\log }_2\frac{|A_k|}{|A|}$$

分支变量的属性水平越多，表示使用该变量越容易获得较大的熵，同时亦代表该分支属性分支特性不显著，因此会倾向选择具有较小熵值的属性为分支变量。而信息增益比的衡量准则倾向于选择具有较小熵值的属性，而不会考虑具有较高信息增益值的属性，特别是当熵值趋近于0时；为了避免，故先计算出所有侯选属性所带来的平均信息增益值，并仅从具有高于平均信息增益值的侯选属性中，找出具有最小熵值的属性作为分支变量。

• Gini系数

Gini系数是衡量数据集合对于所有类别的不纯度，不纯度越小的属性越应该作为分支属性。定义如下：
$$Gini(C)=1-\sum _{k=j}^n{p}_j^2$$
属性A的基尼指数定义为：
$$Gini(C,A)=1-\sum _{i=1}^m\frac{|A_i|}{|A|}Gini(A_i$$