Assignment #1.1 Softmax 分类算法

最新推荐文章于 2024-07-21 07:37:29 发布

Doodlera

最新推荐文章于 2024-07-21 07:37:29 发布

阅读量396

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/qq_35248792/article/details/84839511

本文详细介绍了Softmax函数的实现过程，包括如何避免数值稳定性问题，如处理exp函数的大输入导致的inf问题。通过具体示例展示了如何在向量和矩阵中正确应用Softmax函数，并提供了一个可运行的Python代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

实现Softmax 。本以为十分简单，不想还是遇到了各种问题。
最终的程序如下，如果还有问题再做修正。

  def softmax(x):
    orig_shape = x.shape

    if len(x.shape) > 1:
        # Matrix
        x=np.exp(x-np.max(x,1).reshape(-1,1))/np.sum(np.exp(x-np.max(x,1).reshape(-1,1)),axis=1)            
        #raise NotImplementedError           
    else:
        x=(np.exp(x-max(x)))/np.sum(np.exp(x-max(x)))
        # Vector
        #raise NotImplementedError

    assert x.shape == orig_shape
    return x

提供了三个样例进行检验。

def test_softmax_basic():
    """
    Some simple tests to get you started.
    Warning: these are not exhaustive.
    """
    print ("Running basic tests...")
    test1 = softmax(np.array([1,2]))
    print (test1)
    ans1 = np.array([0.26894142,  0.73105858])
    assert np.allclose(test1, ans1, rtol=1e-05, atol=1e-06)

    test2 = softmax(np.array([[1001,1002],[3,4]]))
    print (test2)
    ans2 = np.array([
        [0.26894142, 0.73105858],
        [0.26894142, 0.73105858]])
    assert np.allclose(test2, ans2, rtol=1e-05, atol=1e-06)

    test3 = softmax(np.array([[-1001,-1002]]))
    print (test3)
    ans3 = np.array([0.73105858, 0.26894142])
    assert np.allclose(test3, ans3, rtol=1e-05, atol=1e-06)

    print ("You should be able to verify these results by hand!\n")

softmax函数公式如下
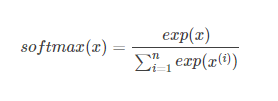
在这里插入图片描述
起初单纯的按照公式来实现。第一个样例没有问题，第二个样例就出现了问题。因为exp函数的输入过大，出现了inf。第一反应是去调整精度（错误做法）。正确做法如下：

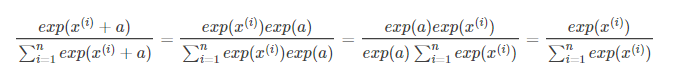
换算后可以正常使用。
（这里多亏了https://blog.youkuaiyun.com/linuxwindowsios/article/details/78003312）
之后的问题是如何实现上述变换。在矩阵的情况下进行实现遇到了问题。
1.如何求出矩阵每行/每列的最大值。

>>>np.max(x,0)  #计算所有列的最大值

>>>np.max(x,1)  #计算所有行的最大值

2.求得的最大值是一个一维向量。需要进行转置。一维向量无法使用.T。使用reshape函数。

>>> a = np.array([1, 2, 3])
>>> a = a.reshape(-1, 1)
>>> a
array([[1],
       [2],
       [3]])

3.sum函数的使用
当axis为0时,是压缩行,即将每一列的元素相加,将矩阵压缩为一行
当axis为1时,是压缩列,即将每一行的元素相加,将矩阵压缩为一列

>>> np.sum([[0, 1], [0, 5]], axis=0)
array([0, 6])
>>> np.sum([[0, 1], [0, 5]], axis=1)
array([1, 5])

4.作业中的raise NotImplementedError 一度困扰我。注释掉后程序就没有问题。