R语言--数据挖掘1---缺失值的识别与处理

第一次作业

缺失值的识别与处理

总的思路：

查看数据，进行分析

-> 有缺失值，则我们分析为什么有缺失值

->分析缺失值的类型

->如何处理这个缺失值，有哪些方法，如何选取这些方法

->对插补之后的缺失值进行评价，即看插补的好不好

查看原始数据

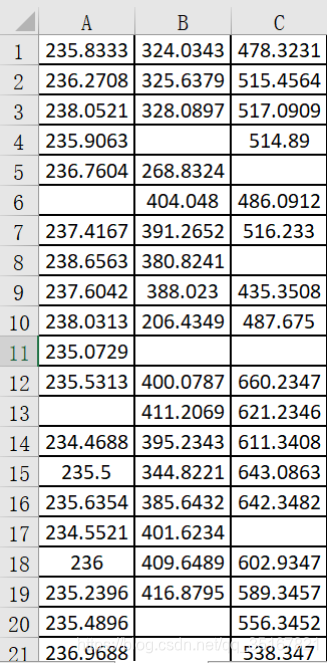
有3个变量（列），21个观测值(行）

如上表所示，用户的用电数据存在有缺失值。

于是我们先考虑使用R语言的mice包来查看数据中缺失值的分布，其中缺失值的分布如下图所示：

分析缺失值的模式及机制

setwd("D:/lagua/CODING/R-learn/R-code/Chap5_model")
data<-read.xlsx("./missing_data.xls", 1, 
                header=0,
                colClasses=rep("numeric",4))
md.pattern(data)

得到缺失值的分布状况

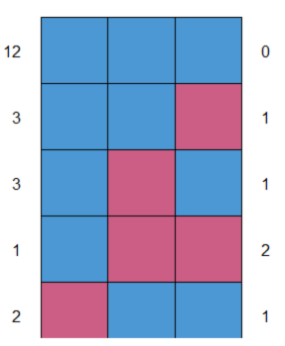
其中的蓝色方块表示正常未缺失的数据，红色方块代表具有缺失值的数据。在上图左列，12,3,3,…等数据代表对应缺失模式的观测数；右列中的0表示数据被观察到，1表示数据未被观察到，即数据缺失。

同时图形显示缺失值的比例与缺失情况：

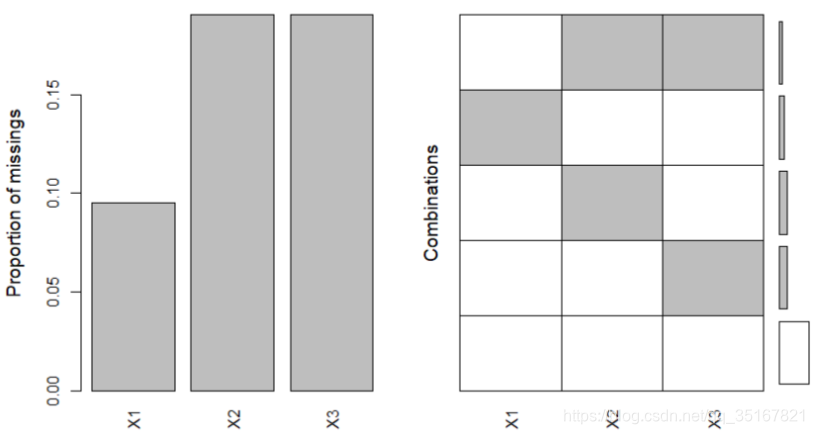
其中，在左图中，灰色的直方图表示各个变量的缺失比例；在右图中，白色部分表示每个变量正常且未缺失的数据，灰色部分表示缺失的数据，右边的竖条表示各种缺失模式所占的比例。

在分析以上缺失数据模式与缺失数据机制之前，先介绍一些几种缺失模式和缺失数据机制。

缺失数据模式

首先，缺失数据模式分为：

• 单变量缺失模式：在所有数据中，只有一个变量有缺失值。
• 单调模式：当前面一个变量具有缺失值时，后面一个变量一定存在有缺失值。
• 一般缺失模式：有多个变量会出现缺失值，但出现缺失值的变量又不是单调模式。

缺失数据机制

缺失数据机制分为以下三种：

1. 完全随机缺失(MCAR)

   完全随机缺失的缺失值的概率分布是
   $$f(\mathcal{M}|\mathcal{Y},\varphi )=f(\mathcal{M}|\varphi ),forany\mathcal{Y},\varphi$$
   它表明，缺失值的关于给定$\mathcal{Y},\varphi$的分布与只给定$\varphi$的分布是一样的，这说明缺失值的$\mathcal{M}$的分布与随机变量$\mathcal{Y}$的分布无关，也就是随机的。

2. 随机缺失(MAR)

   缺失值的分布为
   $$f(\mathcal{M}|\mathcal{Y},\varphi )=f(\mathcal{M}|{\mathcal{Y}}^{obs},\varphi ),forany\mathcal{Y},\varphi$$
   其中${\mathcal{Y}}^{obs}$的是变量$\mathcal{Y}$的观测值。

   以上的分布说明，变量$\mathcal{M}$的分布仅仅依赖于观测数据${\mathcal{Y}}^{obs}$的真实值，不依赖于缺失数据${\mathcal{Y}}^{mis}$。

3. 非随机缺失

   是上面两种情况综合的对立面。说明缺失指示矩阵是依赖于缺失观测数据${\mathcal{Y}}^{mis}$，缺失变量的分布为
   $$f(\mathcal{M}|\mathcal{Y},\varphi )=f(\mathcal{M}|{\mathcal{Y}}^{mis},\varphi ),forany\mathcal{Y},\varphi$$

分析当前数据

由以上两图可以看出，本案例数据三个变量均出现缺失值，确实变量也不是单调模式，所以本案例的缺失数据模式为随机缺失模式。

缺失数据机制：结合这三种缺失数据缺失机制，我们可以知道，每个随机变量与剩下的两个随机变量的缺失都无关，每个变量是否缺失完全是随机的，也就是说是完全随机缺失数据。

处理缺失值

由于当前案例数据是一般的缺失模式，所以我们考虑使用mice方法来插值，本次插补使用R语言中的多重插值包Mice来完成。

其中mice包的插值分析及填补的步骤如下：

1. 得到具有缺失值的数据。
2. mice—使用MCMC方法估计插补值，多此插补(m = 5)，来得到m次插补之后的数据集。
3. with—对每个数据集进行建模，分别使用pmm, cart, rf, mean, norm方法来进行插值。
4. 对所使用的模型进行检验，一般是使用summary(fit)，根据其中得到的p值来判断之前拟合模型的参数是否显著。
5. pool—对参数显著的模型，将这些插值之后的数据整合到一起.
6. 评价插补模型的好坏（模型的t统计量）
7. 根据上面评价，找到一个好的插补之后的数据集/综合之前插补的数据，使用complete函数得到插补之后完整的、无缺失的数据集。

首先先对数据进行画图, 得到下图:

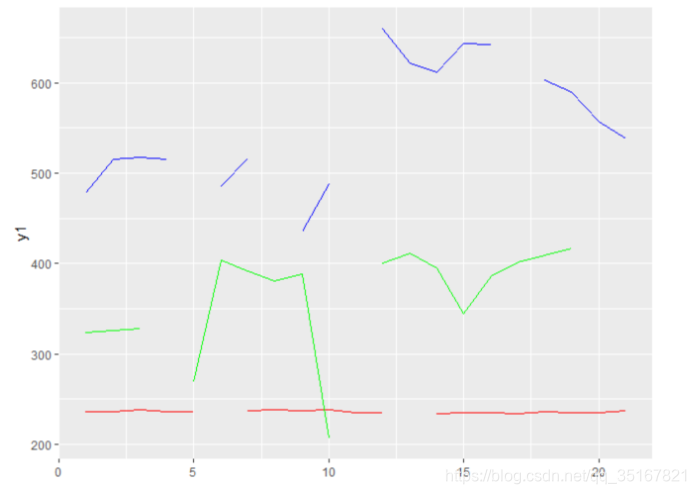
如图所示，红色的表示变量X1，蓝色的表示变量X2，绿色的代表变量X3.

其中X2，X3所代表的数据表明数据观测值表明，数据的波动较大，且没有明显的线性相关关系，且当前数据的缺失模式为一般缺失模式，所以考虑使用R语言中MICE包中的MCMC方法来插补数据；而红的变量表明，X1的波动较小，在进行数据补全时，可考虑使用均值来填补。

接下来开始使用mice包进行插值

# 准备使用mice进行插值
m <- 5
mi_data <- mice(data,m, seed=1)  

mi_data$imp		# 查看插补之后的所有数据
mi_data$imp$X1	# 查看对X1变量插补得到的数据

with分析

参考：https://stefvanbuuren.name/fimd/workflow.html

The with() function handles two tasks: to fill in the missing data and to analyze the data.

它主要有两个功能：将缺失值填到原来的数据中去，以及分析数据，来分析数据（一般是使用回归模型）。

使用with来对插补之后的数据建立回归模型，检验模型的显著性，依次结果来查看插补的效果。

使用lm(X1~1)来检查变量X1的均值和标准差, 来判断插值得到的数据好坏.

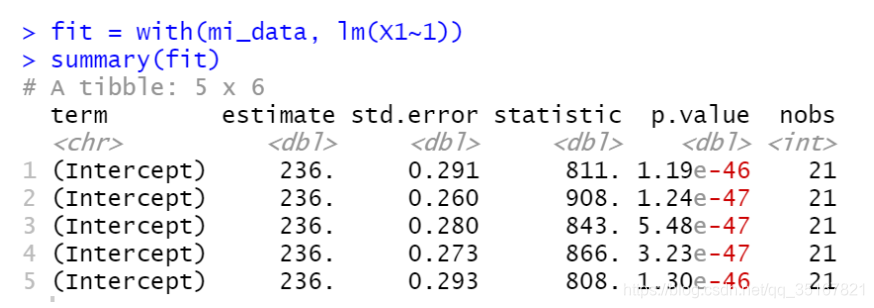
如图所示,变量X1所有的p.value均远小于0.01, 且变量的标准误差都不大, 所以在综合所有数据的插值来求均值, 来作为对最后插值的估计是合适的.

以下继续对变量X2进行检验:

如图所示,变量X2所有的p.value均远小于0.01, 且变量的标准误差都相差不大, 所以在综合所有数据的插值来求均值, 来作为对最后插值的估计是合适的.

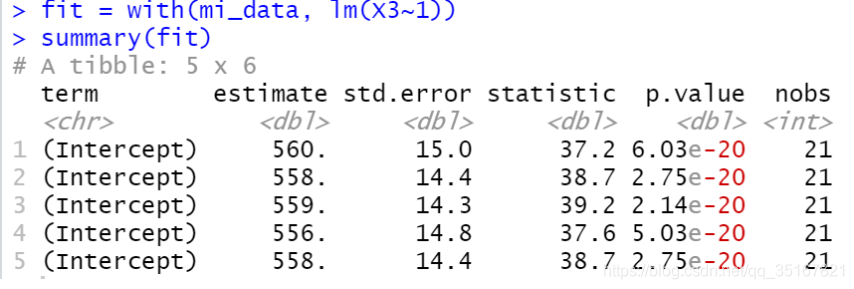
以下是对变量X3的检验:

如图所示,变量X3所有的p.value均远小于0.01, 且变量的标准误差都相差不大, 所以在综合所有数据的插值来求均值, 来作为对最后插值的估计是合适的.

综合上面三个回归的分析, 可知所有的插值的方差是差不多大的，而且所有插值的p值均远小于0.01，初步判定插值合适，所以在接下来的pool函数将所有的插值都整合到一起。

根据以上对回归模型的分析，最后选择使用所有回归标准差最小的一个插值，也就是第二次插值。

将当前的数据导出到excel表格中

complete.data = complete(mi_data, 2)
write.table(complete.data, file='./complete_data.xls',row.names = F,quote=F, sep="\t")

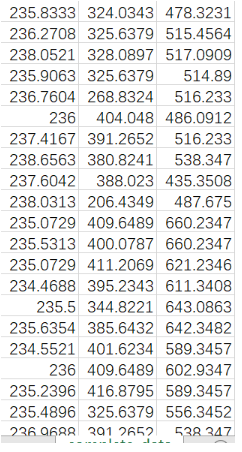
最后数据:

插补值的评价

以上查看缺失值插补值之后原始变量的分布情况只是一个初始的插补值的评价，关于具体插补值具体插补的好坏，还需要通过以后建立模型来预测或者回归来进一步检验插补值的效果。

总的代码

# 导入包
library(mice)   
library(VIM)                                      
library(dplyr)
library(xlsx)
# 读取数据
setwd("D:/lagua/CODING/R-learn/R-code/Chap5_model")
data<-read.xlsx("./missing_data.xls", 1, 
                header=0,
                colClasses=rep("numeric",4))
# 查看数据
data
summary(data)
md.pattern(data)

aggr(data,prop=T,numbers=T,col=c('blue','red'))  

# 准备使用mice进行插值
m <- 5

mi_data <- mice(data,m, seed=1)  

mi_data$imp
mi_data$imp$X1
help(mice)

cor(data[complete.cases(data)==T,])

# ------------------plot-------------------
library(tidyverse)
library(ggplot2)

x = seq(1, 21, 1)
help(sep)
x = seq(1, 21, 1)
X = data[, 1]
X2 = data[, 2]
X3 = data[, 3]
# ,labels=paste("X",seq(1, 3, 1),sep="")
ggplot(data=data)+
  geom_line(mapping=aes(x=x,y=X),data=data,show.legend=TRUE,color="red")+
  geom_line(mapping=aes(x=x,y=X2),data=data,show.legend=TRUE,color="blue")+
  geom_line(mapping=aes(x=x, y=X3),data=data,show.legend=TRUE,color="green")+
  guides(fill=guide_legend())

# 对第一个自变量X1自身建立回归模型
fit = with(mi_data, lm(X1~1))
fit %>% pool() %>% summary()

# 对第一个自变量X3自身建立回归模型
fit = with(mi_data, lm(X2~1))
fit %>% pool() %>% summary()

# 对第一个自变量X3自身建立回归模型
fit = with(mi_data, lm(X3~1))
fit %>% pool() %>% summary()

complete.data = complete(mi_data, 2)
write.table(complete.data, file='./complete_data.xls',row.names = F,quote=F, sep="\t")

参考

R语言：用R语言填补缺失的数据
R语言︱缺失值处理之多重插补——mice包
缺失值处理（r语言，mice包）
用R语言填充缺失值mice
R语言处理缺失数据的高级方法

r语言，mice包）](https://cloud.tencent.com/developer/article/1089158?from=information.detail.r%E8%AF%AD%E8%A8%80mice)
用R语言填充缺失值mice
R语言处理缺失数据的高级方法

Flexible imputation of Missing Data