leetcode 2846.边权重均等查询

最新推荐文章于 2025-05-09 14:48:06 发布
最新推荐文章于 2025-05-09 14:48:06 发布
阅读量1.8k 收藏 23
点赞数 41
分类专栏： 力扣刷题 文章标签： leetcode 算法
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_35085273/article/details/135883128
版权

题目

现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。

另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条边，并将其权重更改为任意值。

注意：

  • 查询之间 相互独立 的，这意味着每条新的查询时，树都会回到 初始状态 。
  • 从 ai 到 bi的路径是一个由 不同 节点组成的序列，从节点 ai 开始，到节点 bi 结束，且序列中相邻的两个节点在树中共享一条边。

返回一个长度为 m 的数组 answer ，其中 answer[i] 是第 i 条查询的答案。

示例 1：

输入：n = 7, edges = [[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]], queries = [[0,3],[3,6],[2,6],[0,6]]
输出：[0,0,1,3]
解释：第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1 。因此，答案为 0 。
第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 0 。
第 3 条查询，将边 [2,3] 的权重变更为 2 。在这次操作之后，从节点 2 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 1 。
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2 。在这次操作之后，从节点 0 到节点 6 的路径中的所有边的权重都是 2 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

示例 2：

输入：n = 8, edges = [[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]], queries = [[4,6],[0,4],[6,5],[7,4]]
输出：[1,2,2,3]
解释：第 1 条查询，将边 [1,3] 的权重变更为 6 。在这次操作之后，从节点 4 到节点 6 的路径中的所有边的权重都是 6 。因此，答案为 1 。
第 2 条查询，将边 [0,3]、[3,1] 的权重变更为 6 。在这次操作之后，从节点 0 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 3 条查询，将边 [1,3]、[5,2] 的权重变更为 6 。在这次操作之后，从节点 6 到节点 5 的路径中的所有边的权重都是 6 。因此，答案为 2 。
第 4 条查询，将边 [0,7]、[0,3]、[1,3] 的权重变更为 6 。在这次操作之后，从节点 7 到节点 4 的路径中的所有边的权重都是 6 。因此，答案为 3 。
对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。

提示：

  • 1 <= n <= 104
  • edges.length == n - 1
  • edges[i].length == 3
  • 0 <= ui, vi < n
  • 1 <= wi <= 26
  • 生成的输入满足 edges 表示一棵有效的树
  • 1 <= queries.length == m <= 2 * 104
  • queries[i].length == 2
  • 0 <= ai, bi < n

思路

这道每日例题是一个高难度dfs，现在分为几个部分整理下思路：

本地测试定义和引用：

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct Node Node_t;

#define fail 0
#define succ 1
#define true 1
#define false 0

main函数

经过打印测试，获取参数值，得到本地测试main函数：

int main(void)
{
    int edges[][3] = {{1,2,6},{1,3,4},{2,4,6},{2,5,3},{3,6,6},{3,0,8},{7,0,2}};
    int edgesSize = sizeof(edges)/sizeof(edges[0]);
    int edgesColSize = 3;
    int n = 8;
    int queries[][2] = {{4,6},{0,4},{6,5},{7,4}};
    
    int queriesSize = sizeof(queries)/sizeof(queries[0]);
    int queriesColSize = 2;
    int returnSize = 0;
    int *result = minOperationsQueries(n, edges, edgesSize, &edgesColSize, queries, queriesSize, &queriesColSize, &returnSize);
    for (int i = 0; i < returnSize; i++)
    {
        printf("result[%d] = %d\n",i, result[i]);
    }
    free(result);
    return 0;
}

数据类型定义

定义两个结构体：node和my_st,用于存储随机生成的树节点信息和查完路径后计算最多出现的那个路径长度的出现次数。叫my_st是因为不知道起什么名字好。

typedef struct Node
{
    int index;
    Node_t* prev;
    Node_t* left;
    Node_t* right;
    int lenToPrev;
    int lenToLeft;
    int lenToRight;
    _Bool isViaThisTurn;
} Node_t;


typedef struct 
{
    int len;
    int appearTime;
}my_st;

getDistance函数，

函数目的：

给定一个指向节点的指针（通过指向指针的指针传递），以及一个目标节点的索引，函数尝试找到从给定节点到目标节点的路径长度，并将指向节点的指针更新为目标节点。

参数：

from：一个指向指针的指针，指向起始节点。
toIndex：目标节点的索引。

返回值：

如果找到目标节点，则返回从给定节点到目标节点的路径长度。如果未找到目标节点，则返回0，本题目中保证输入一定能构成树，因此这个return0仅仅是为了防止编译warning。

函数流程：

首先通过解引用 from 得到起始节点 tmp_node。
然后，在leftson，rightson，prev非空的情况下检查谁是目标节点，然后返回到目标节点的距离，因为在findway中把路径已经直接存好了，所以这个函数没那么多检查，其实可以把他融合进findway中，但是这样不好看，权当解耦用了。

复杂度分析：

时间复杂度：O(1)；
空间复杂度：O(1)；

可能遇到的坑：

1、要用双重指针保证返回去之后from的值改变，不然起不到实时更新寻路，得在外面修改，很麻烦；

2、查tmp->x->index的时候一定要检查tmp->x是不是NULL，不然直接崩掉；

3、虽然情况一定只有三种，第三个if可以不写，但是可读性，所以写下。


int getDistance(Node_t** from, int toIndex)
{
    Node_t* tmp_node = (*from);
    if(tmp_node->left != NULL)
    if(tmp_node->left->index == toIndex)
    {
        (*from) = tmp_node->left;
        // printf("[%d]dist = %d\n", __LINE__,(*from)->lenToPrev);
        return (*from)->lenToPrev;
    }
    if(tmp_node->right != NULL)
    if(tmp_node->right->index == toIndex)
    {
        (*from) = tmp_node->right;
        // printf("[%d]dist = %d\n", __LINE__,(*from)->lenToPrev);
        return (*from)->lenToPrev;
    }
    if(tmp_node->prev != NULL)
    if(tmp_node->prev->index == toIndex)
    {
        int rc = 0;
        rc = (*from)->lenToPrev;
        (*from) = tmp_node->prev;
        // printf("[%d]dist = %d\n", __LINE__,rc);
        return rc;
    }
    return 0;
}

cntChange函数

函数目的：

给定一个路径（以数组 way 表示），起始节点 from，以及路径上节点的数量 n，函数计算路径中相邻节点之间距离的变化次数。

参数：

way：表示路径的数组。
n：路径上节点的数量。
from：起始节点。

返回值：

返回路径中距离变化的次数。这里的距离是通过 getDistance 函数计算得到的。

函数流程：

函数首先定义了一个结构体数组 len，每个元素表示一个距离值及其出现的次数。
使用 memset 将 len 数组初始化为零。
然后，函数遍历路径数组 way，对于每一对相邻节点，通过调用 getDistance 函数计算它们之间的距离 dist。
接着，函数检查 dist 是否已经出现过，如果是，则增加其出现次数；否则，在 len 数组中找到一个空闲位置记录 dist 及其出现次数。
最后，函数遍历 len 数组，找到出现次数最多的距离，并返回路径上距离变化的次数。

复杂度分析：

时间复杂度：主要时间消耗在遍历路径数组和调用 getDistance 函数上，因此时间复杂度取决于路径长度和 getDistance 函数的复杂度。因为getDistance是O(1)，所以整体的时间复杂度是 O(n)，其中 n 是路径上的节点数量。
空间复杂度：除了输入参数外，函数使用了一个大小为 n 的结构体数组 len，因此空间复杂度为 O(n)。

可能遇到的坑：

1、记得memset len数组，不然怪数据直接爆炸；

2、一定要在while里面设置index < n这个条件，不然way拉满了的话，可能会跟着怪东西；

3、return的时候(index == n) ? (index - maxTime - 1) : (index - maxTime)，假如way没拉满中途出来了还好，假如拉满了会导致index = n，这样就会比咱的数组索引大一位，导致结果错掉；

int cntChange(int* way,int n,Node_t* from)
{
    int index = 0;
    int rc = 0;
    my_st len[n];
    int dist = 0;
    memset(len, 0, sizeof(len));
    while (way[index] != -1 && way[index + 1] != -1 && index < n)
    {
        // printf("find dist from %d to %d\n", from->index,way[index + 1]);
        dist = getDistance(&from, way[index + 1]);
        index++;
        int saved = 0;
        for (int i = 0; i < n; i++)
        {
            if(len[i].len == dist)
            {
                len[i].appearTime++;
                saved = 1;
            }
        }
        if(saved == 0)
        {
            for (int i = 0; i < n; i++)
            {
                if(len[i].len == 0)
                {
                    len[i].len = dist;
                    len[i].appearTime = 1;
                    break;
                }
            }
        }
    }
    int maxTime = 0;
    for (int i = 0; i < n; i++)
    {
        if(len[i].len == 0)
        {
            continue;
        }
        // printf("len[%d] = %d, appear %d\n", i, len[i].len, len[i].appearTime);
        if (maxTime < len[i].appearTime)
        {
            maxTime = len[i].appearTime;
        }
    }
    return (index == n) ? (index - maxTime - 1) : (index - maxTime);
}

findWay函数

函数目的：

给定一个起始节点 now 和目标节点 to，函数尝试在树结构中找到从起始节点到目标节点的路径，并将路径记录在 way 数组中。这个就是我们最主要的DFS函数了，虽然感觉复杂的地方并不是dfs，但是谁叫它是咱题目的核心呢。

参数：

way：一个指向指针的指针，用于存储路径。
now：当前节点。
to：目标节点。
way_p：一个指向整数的指针，表示当前路径的指针。

返回值：

如果找到路径，则返回 succ（成功），否则返回 fail（失败）。

函数流程：

函数首先将当前节点的索引添加到路径数组中，并将当前节点标记为已经访问。
然后，函数检查当前节点的leftson节点、rightson节点和prev节点是否为目标节点，如果是，则将目标节点的索引添加到路径数组中并返回成功。
如果当前节点的子节点不是目标节点且尚未被访问过，则递归调用 findWay 函数，继续向下搜索路径。
如果在当前节点的所有子节点和父节点都未找到目标节点，则函数将当前路径指针恢复，并返回失败。

复杂度分析：

时间复杂度：由于函数是在树结构中搜索路径，其时间复杂度取决于树的结构以及搜索路径的长度。在最坏情况下，可能需要遍历树的所有节点，因此时间复杂度可能是 O(n)，其中 n 是树中的节点数量。
空间复杂度：函数中使用了递归调用，并且维护了路径数组 way，因此空间复杂度取决于树的深度和路径的长度，可能是 O(h + n)，其中 h 是树的高度，n 是路径的长度。

可能遇到的坑：

1、这个函数其实思路很清晰的，主要就是way和way_p操作的时候要注意，后面son和prev都查完了回溯的时候要把way用tmp恢复；

2、一开始没有记录是否已经访问过，过思路的时候才发现可能会出现son，prev来回查，差点死循环；

3、还是那句，访问节点参数的时候一定要检查是否为NULL，不然崩掉；

_Bool findWay(int** way, Node_t* now, Node_t* to, int* way_p)
{
    // printf("find %d to %d\n",now->index,to->index);
    _Bool rc = fail;
    int *tmp = way_p;
    way_p[0] = now->index;
    now->isViaThisTurn = true;
    // printf("%d is visited\n", now->index);
    if(now->left == to || now->right == to || now->prev == to)
    {
        way_p[1] = to->index;
        return succ;
    }
    way_p++;



    if((now->left != NULL) && (!now->left->isViaThisTurn))
    {
        // printf("try to %d\n",now->left->index);
        rc = findWay(way,now->left,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->left->index);
    }
    
    if((now->right != NULL) && (!now->right->isViaThisTurn))
    {
        // printf("try to %d\n",now->right->index);
        rc = findWay(way,now->right,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->right->index);
    }
    
    if((now->prev != NULL) && (!now->prev->isViaThisTurn))
    {
        // printf("try to %d\n",now->prev->index);
        rc = findWay(way,now->prev,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->prev->index);
    }
    way_p = tmp;
    return rc;
}

minOperationsQueries函数

函数目的：

咱的主要解题函数，也是最难的绘图函数，这个题目我觉得难点就在于怎么把这个输入的边组成一棵树，其实画图可以另写一个函数，但是这样还得传一堆东西过去，就算了。给定图的节点数量 n，边的信息 edges，查询的信息 queries，以及相应的大小信息，函数执行一系列操作和查询，并返回结果数组。

参数：

n：图中节点的数量。
edges：表示图中边的信息。
edgesSize：边的数量。
edgesColSize：边信息数组的列数。
queries：表示查询的信息。
queriesSize：查询的数量。
queriesColSize：查询信息数组的列数。
returnSize：返回结果数组的大小。

返回值：

返回一个指向整数的指针result。

函数流程：

函数首先创建了一个 Node_t 类型的数组 nodes，用于表示图中的节点。
然后，函数将边信息和查询信息复制到局部数组 edg 和 que 中。//这个操作本来不用的，但是不这么操作好像会指针飞掉，不知道为什么。
接下来，函数遍历边信息数组 edg，并根据边的起始节点和目标节点建立图的连接关系。
在建立连接关系时，根据节点的左右子节点或父节点是否为空，选择合适的连接方式，并更新节点的相关属性。
然后，函数遍历查询信息数组 que，对每个查询调用 findWay 函数查找起始节点到目标节点的路径，并调用 cntChange 函数计算路径上的变化次数。
最后，函数将结果存储在结果数组中，并返回。

复杂度分析：

时间复杂度：主要时间消耗在建立图的连接关系和执行查询上。建立连接关系的时间复杂度取决于边的数量，而执行查询的时间复杂度取决于查询的数量和查询路径的复杂度。因此，总体时间复杂度可能是 O(edgesSize + queriesSize * (n + m))，其中 m 是查询路径的平均长度。差不多是O(n^2)级别的（不知道算的对不对）。
空间复杂度：函数中使用了几个局部数组和一个节点数组，以及结果数组。因此，空间复杂度取决于这些数组的大小，可能是 O(n + edgesSize + queriesSize + m)，其中 m 是查询路径的最大长度。

可能遇到的坑：

坑死了。。。

1、声明int edg[edgesSize][*edgesColSize]，Node_t nodes[n]这种可变数组不能直接 = {0}初始化，得memset（虽然我这边直接cpy了）（而且老码农应该都知道）;

2、要用*edgesColSize和*queriesColSize，直接用的话是个地址，巨大，直接崩掉；

3、nodes要初始化，不然会有怪东西；

4、绘图的时候，记得加上nodes[indexB].prev == NULL！！！记得加上nodes[indexB].prev == NULL！！！记得加上nodes[indexB].prev == NULL！！！我一开始没加，导致部分节点两个爹，直接把第一个爹刷掉导致树断掉，，查了好久。

如图：

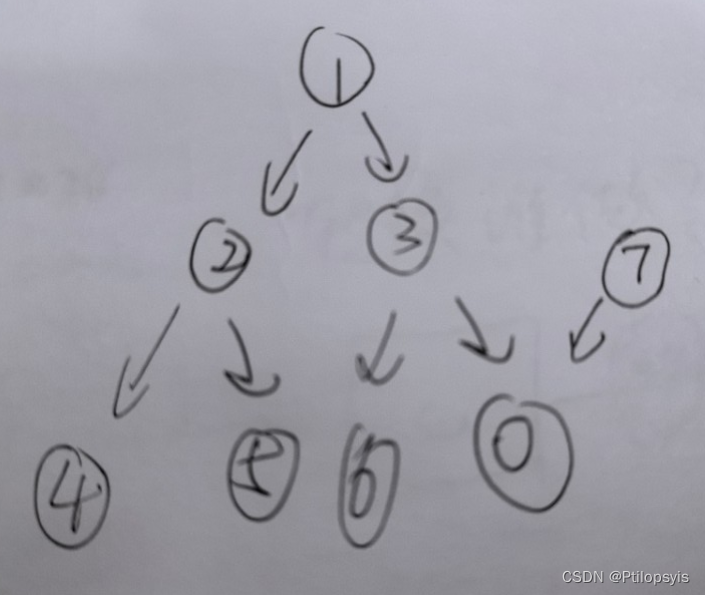
5、这段和后面的其实本来我一开始是leftson和rightson满了直接找prev的，但是为了查4改掉了，一开始没发现是4的问题；

int tmp = indexA;
indexA = indexB;
indexB = tmp;

6、这边memset(way, -1, sizeof(way));要给初始化-1，因为节点是包含index = 0的情况的；

7、当然别忘了(*returnSize)++;

8、查完一个que记得清空isViaThisTurn，不然下轮直接炸裂；

9、别忘了return result;（不会有人忘了return把，是我啊，那没事了。

int* minOperationsQueries(int n, int** edges, int edgesSize, int* edgesColSize, int** queries, int queriesSize, int* queriesColSize, int* returnSize){
    Node_t nodes[n];
    int edg[edgesSize][*edgesColSize];
    int que[queriesSize][*queriesColSize];
    memcpy(edg, edges, sizeof(edg));
    memcpy(que, queries, sizeof(que));
    int * result = (int*)malloc(queriesSize * sizeof(int));
    memset(nodes, 0, sizeof(nodes));
    for (int i = 0; i < n; i++)
    {
        nodes[i].index = i;
    }
    // printf("edgesSize = %d, edgesColSize = %d, queriesSize = %d, queriesColSize = %d\n", edgesSize, *edgesColSize, queriesSize, *queriesColSize);
    // return result; //test
    for (int i = 0; i < edgesSize; i++)
    {
        int indexA = edg[i][0];
        int indexB = edg[i][1];
        if(nodes[indexA].left == NULL && nodes[indexB].prev == NULL)
        {
            nodes[indexA].left = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToLeft = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        if(nodes[indexA].right == NULL && nodes[indexB].prev == NULL)
        {
            nodes[indexA].right = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToRight = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        int tmp = indexA;
        indexA = indexB;
        indexB = tmp;
        if(nodes[indexA].left == NULL)
        {
            nodes[indexA].left = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToLeft = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        if(nodes[indexA].right == NULL)
        {
            nodes[indexA].right = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToRight = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
    }
    int index = 0;
    for (int i = 0; i < queriesSize; i++)
    {
        int indexFrom = que[i][0];
        int indexTo =  que[i][1];
        // printf("\nfindway %d to %d\n",indexFrom,indexTo);
        int way[n];
        int *way_p = way;
        memset(way, -1, sizeof(way));
        findWay((int**)&way, &nodes[indexFrom], &nodes[indexTo], way_p);
        // printf("way is [");
        // for(int j = 0;j < n;j++)
        // {
        //     printf("%d ",way[j]);
        // }
        // printf("]\n\n\n");
        result[index] = cntChange(way,n,&nodes[indexFrom]);
        (*returnSize)++;
        index++;
        for (int j = 0; j < n; j++)
        {
            nodes[j].isViaThisTurn = false;
        }
    }
    return result;
}

代码

以下是总代码，带了调试打印的。

/**
 * Note: The returned array must be malloced, assume caller calls free().
 */
//edgesSize边个数 
//edgesColSize 3
//queriesSize查询个数
//queriesColSize 2
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
typedef struct Node Node_t;

typedef struct Node
{
    int index;
    Node_t* prev;
    Node_t* left;
    Node_t* right;
    int lenToPrev;
    int lenToLeft;
    int lenToRight;
    _Bool isViaThisTurn;
} Node_t;


typedef struct 
{
    int len;
    int appearTime;
}my_st;


#define fail 0
#define succ 1
#define true 1
#define false 0

int getDistance(Node_t** from, int toIndex)
{
    Node_t* tmp_node = (*from);
    if(tmp_node->left != NULL)
    if(tmp_node->left->index == toIndex)
    {
        (*from) = tmp_node->left;
        // printf("[%d]dist = %d\n", __LINE__,(*from)->lenToPrev);
        return (*from)->lenToPrev;
    }
    if(tmp_node->right != NULL)
    if(tmp_node->right->index == toIndex)
    {
        (*from) = tmp_node->right;
        // printf("[%d]dist = %d\n", __LINE__,(*from)->lenToPrev);
        return (*from)->lenToPrev;
    }
    if(tmp_node->prev != NULL)
    if(tmp_node->prev->index == toIndex)
    {
        int rc = 0;
        rc = (*from)->lenToPrev;
        (*from) = tmp_node->prev;
        // printf("[%d]dist = %d\n", __LINE__,rc);
        return rc;
    }
    return 0;
}


int cntChange(int* way,int n,Node_t* from)
{
    int index = 0;
    int rc = 0;
    my_st len[n];
    int dist = 0;
    memset(len, 0, sizeof(len));
    while (way[index] != -1 && way[index + 1] != -1 && index < n)
    {
        // printf("find dist from %d to %d\n", from->index,way[index + 1]);
        dist = getDistance(&from, way[index + 1]);
        index++;
        int saved = 0;
        for (int i = 0; i < n; i++)
        {
            if(len[i].len == dist)
            {
                len[i].appearTime++;
                saved = 1;
            }
        }
        if(saved == 0)
        {
            for (int i = 0; i < n; i++)
            {
                if(len[i].len == 0)
                {
                    len[i].len = dist;
                    len[i].appearTime = 1;
                    break;
                }
            }
        }
    }
    int maxTime = 0;
    for (int i = 0; i < n; i++)
    {
        if(len[i].len == 0)
        {
            continue;
        }
        // printf("len[%d] = %d, appear %d\n", i, len[i].len, len[i].appearTime);
        if (maxTime < len[i].appearTime)
        {
            maxTime = len[i].appearTime;
        }
    }
    return (index == n) ? (index - maxTime - 1) : (index - maxTime);
}

_Bool findWay(int** way, Node_t* now, Node_t* to, int* way_p)
{
    // printf("find %d to %d\n",now->index,to->index);
    _Bool rc = fail;
    int *tmp = way_p;
    way_p[0] = now->index;
    now->isViaThisTurn = true;
    // printf("%d is visited\n", now->index);
    if(now->left == to || now->right == to || now->prev == to)
    {
        way_p[1] = to->index;
        return succ;
    }
    way_p++;



    if((now->left != NULL) && (!now->left->isViaThisTurn))
    {
        // printf("try to %d\n",now->left->index);
        rc = findWay(way,now->left,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->left->index);
    }
    
    if((now->right != NULL) && (!now->right->isViaThisTurn))
    {
        // printf("try to %d\n",now->right->index);
        rc = findWay(way,now->right,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->right->index);
    }
    
    if((now->prev != NULL) && (!now->prev->isViaThisTurn))
    {
        // printf("try to %d\n",now->prev->index);
        rc = findWay(way,now->prev,to,way_p);
        if(rc == succ)
        {
            return rc;
        }
        // printf("[%d]way to %d is invalid\n",__LINE__,now->prev->index);
    }
    way_p = tmp;
    return rc;
}

int* minOperationsQueries(int n, int** edges, int edgesSize, int* edgesColSize, int** queries, int queriesSize, int* queriesColSize, int* returnSize){
    Node_t nodes[n];
    int edg[edgesSize][*edgesColSize];
    int que[queriesSize][*queriesColSize];
    memcpy(edg, edges, sizeof(edg));
    memcpy(que, queries, sizeof(que));
    int * result = (int*)malloc(queriesSize * sizeof(int));
    memset(nodes, 0, sizeof(nodes));
    for (int i = 0; i < n; i++)
    {
        nodes[i].index = i;
    }
    // printf("edgesSize = %d, edgesColSize = %d, queriesSize = %d, queriesColSize = %d\n", edgesSize, *edgesColSize, queriesSize, *queriesColSize);
    // return result; //test
    for (int i = 0; i < edgesSize; i++)
    {
        int indexA = edg[i][0];
        int indexB = edg[i][1];
        if(nodes[indexA].left == NULL && nodes[indexB].prev == NULL)
        {
            nodes[indexA].left = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToLeft = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        if(nodes[indexA].right == NULL && nodes[indexB].prev == NULL)
        {
            nodes[indexA].right = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToRight = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        int tmp = indexA;
        indexA = indexB;
        indexB = tmp;
        if(nodes[indexA].left == NULL)
        {
            nodes[indexA].left = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToLeft = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
        if(nodes[indexA].right == NULL)
        {
            nodes[indexA].right = &nodes[indexB];
            nodes[indexB].prev = &nodes[indexA];
            nodes[indexA].lenToRight = edg[i][2];
            nodes[indexB].lenToPrev = edg[i][2];
            continue;
        }
    }
    int index = 0;
    for (int i = 0; i < queriesSize; i++)
    {
        int indexFrom = que[i][0];
        int indexTo =  que[i][1];
        // printf("\nfindway %d to %d\n",indexFrom,indexTo);
        int way[n];
        int *way_p = way;
        memset(way, -1, sizeof(way));
        findWay((int**)&way, &nodes[indexFrom], &nodes[indexTo], way_p);
        // printf("way is [");
        // for(int j = 0;j < n;j++)
        // {
        //     printf("%d ",way[j]);
        // }
        // printf("]\n\n\n");
        result[index] = cntChange(way,n,&nodes[indexFrom]);
        (*returnSize)++;
        index++;
        for (int j = 0; j < n; j++)
        {
            nodes[j].isViaThisTurn = false;
        }
    }
    return result;
}

int main(void)
{
    int edges[][3] = {{1,2,6},{1,3,4},{2,4,6},{2,5,3},{3,6,6},{3,0,8},{7,0,2}};
    int edgesSize = sizeof(edges)/sizeof(edges[0]);
    int edgesColSize = 3;
    int n = 8;
    int queries[][2] = {{4,6},{0,4},{6,5},{7,4}};
    
    int queriesSize = sizeof(queries)/sizeof(queries[0]);
    int queriesColSize = 2;
    int returnSize = 0;
    int *result = minOperationsQueries(n, edges, edgesSize, &edgesColSize, queries, queriesSize, &queriesColSize, &returnSize);
    for (int i = 0; i < returnSize; i++)
    {
        printf("result[%d] = %d\n",i, result[i]);
    }
    free(result);
    return 0;
}

结果

不知道为啥，丢到leetcode上总是报指针飞掉，本地就可以跑，

跑了测试用例，东西都是对的，

用例1：

7
[[0,1,1],[1,2,1],[2,3,1],[3,4,2],[4,5,2],[5,6,2]]
[[0,3],[3,6],[2,6],[0,6]]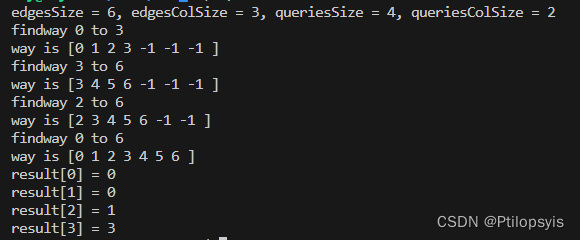

用例2：

8
[[1,2,6],[1,3,4],[2,4,6],[2,5,3],[3,6,6],[3,0,8],[7,0,2]]
[[4,6],[0,4],[6,5],[7,4]]


Leetcode 超难题目 Hard
yake1965
01-05 1307
这道题很有可能是LC主站（LCP除外）新的天花板，之所以难度分没有超过1719题，是因为双周赛样本量本身不多，而这题有一定的“猜结论”。某个LC积分2900+的大佬认为，即使数据范围只有1000，这也是一道相当难的题目。因为记录dp[j]为最优时，nums[j]的最小值（注意nums[j]很可能是被改过的），这样的DP本身就很难想到。而同时保证dp[j]最大nums[j]最小是否就更利于后面的转移，这点非常难证明。这个题的数据范围并不是1000，因此需要单调数据结构优化来保证复杂度合理。
算法笔记|leetcode刷题记录（C++）
JormungandrN的博客
06-11 573
刷题记录
【Leetcode】2846. 边权重均等查询
想要AC的sjh的博客空间
01-26 993
每日一题
倍增LCA，LeetCode 2846. 边权重均等查询
EQUINOX1的博客
01-26 1282
典型LCA问题
LC 2846. 边权重均等查询
qq_74040620的博客
01-26 1238
2846. 边权重均等查询
2846. 边权重均等查询
NEFU AB-IN's Blog
07-27 646
Leetcode 2846. 边权重均等查询
【深度优先】【树上倍增 】2846. 边权重均等查询
闻缺陷则喜何志丹
04-05 903
现有一棵由 n 个节点组成的无向树，节点按从 0 到 n - 1 编号。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi, wi] 表示树中存在一条位于节点 ui 和节点 vi 之间、权重为 wi 的边。 另给你一个长度为 m 的二维整数数组 queries ，其中 queries[i] = [ai, bi] 。对于每条查询，请你找出使从 ai 到 bi 路径上每条边的权重相等所需的 最小操作次数 。在一次操作中，你可以选择树上的任意一条
leetcode.2846. 边权重均等查询【lca+树形dp】
lianxuhanshu_的博客
01-26 1619
第 4 条查询，将边 [0,1]、[1,2]、[2,3] 的权重变更为 2。对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。对于每条查询 queries[i] ，可以证明 answer[i] 是使从 ai 到 bi 的路径中的所有边的权重相等的最小操作次数。第 1 条查询，从节点 0 到节点 3 的路径中的所有边的权重都是 1。第 2 条查询，从节点 3 到节点 6 的路径中的所有边的权重都是 2。
每日coding 2846. 边权重均等查询 236. 二叉树的最近公共祖先 35. 搜索插入位置 215. 数组中的第K个最大元素 2. 两数相加
fzx12138的博客
01-26 931
xs，已放弃，考到直接寄。
每日一题 力扣2846 边权重均等查询
kawhixiao的博客
01-26 1418
树实际上就是图论中的有向无环图，而要研究LCA问题，首先我们要指定树中的一个顶点为根节点，并以该节点遍历有向无环图，生成一颗DFS序下的树，假设我们要查询的两个节点为u,v，DFS序下根节点到两点的最短路径分别是(r,u),和(r,v)，LCA就是(r,u)与(r,v)公共路径的最后一个节点。而求两点间的路径长度，可以通过倍增法求 LCA 来实现。要我们以queries数组为遍历基础，先找到ai到bi的路径，然后统计路径上的权值，找到频次最高的权值出现的次数，用路径长度-频次即为所求的最小操作次数。
【力扣每日一题】力扣2846边权重均等查询
qq_56460466的博客
01-26 452
或许在构建树的时候进行旋转，最终把树构建成平衡树结果会好一点。最后看了官方答案，要使用到Tarjan算法，这个算法没有听说过，目前还没有时间，后面有空再进行学习吧。
LeetCode刷题汇总
热门推荐
weixin_44171872的博客
09-19 2万+
剑指offer 剑指 Offer 03 数组中重复的数字 剑指 Offer 04 二维数组中的查找 剑指 Offer 05 替换空格 剑指 Offer 06 从尾到头打印链表 剑指 Offer 07 重建二叉树 剑指 Offer 09 用两个栈实现队列 剑指 Offer 10- I 斐波那契数列 剑指 Offer 10- II 青蛙跳台阶问题 剑指 Offer 11 旋转数组的最小数字 剑指 Offer 12 矩阵中的路径 剑指 Offer 13 机器人的运动范围 剑指 Offer 14- I 剪绳子 剑指
使用TensorFlow 2.0+和Keras实现AlexNet CNN架构
weixin_26752765的博客
09-05 2032
技术 (Technical) 介绍 (Introduction) The main content of this article will present how the AlexNet Convolutional Neural Network(CNN) architecture is implemented using TensorFlow and Keras. 本文的主要内容将介绍如何使...
【建议收藏】50 道硬核的 Python 面试题
k15778864599的博客
09-18 695
题目001: 在Python中如何实现单例模式。方法一：使用装饰器实现单例模式。 方法二：使用元类实现单例模式。 题目002：不使用中间变量，交换两个变量`a`和`b`的值。方法一： 方法二： 题目003：写一个删除列表中重复元素的函数，要求去重后元素相对位置保持不变。 如果愿意也可以把上面的函数改造成一个生成器，代码如下所示。 题目004：假设你使用的是官方的CPython，说出下面代码的运行结果。 运行结果： 上面代码中的结果是但的结果是，这一点的确让人费
双指针算法详解（含力扣和蓝桥杯例题）
m0_74655006的博客
05-03 1303
双指针一般是由快慢指针和对撞指针这两部分组成，其中快慢指针一般是比对撞指针要难一些，我们需要通过题目的意思来设置合适的条件。然后枚举每一种情况就行。
每日一道leetcode
XiaoyaoCarter的博客
05-07 1136
T0 = 0, T1 = 1, T2 = 1, 且在 n >= 0 的条件下 Tn+3 = Tn + Tn+1 + Tn+2。，请返回第 n 个泰波那契数 Tn 的值。
LeetCode 300. 最长递增子序列
YGGP的博客
05-08 243
LeetCode 300. 最长递增子序列。
力扣-24.两两交换链表中的结点
最新发布
weixin_46878941的博客
05-09 216
给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。小结：后来才看到不能修改结点值，但是也不难。
LeetCode 128. 最长连续序列（Java）
2301_79966297的博客
05-07 561
暴力解法（如排序后遍历）的时间复杂度为 O(n log n)，不满足题目要求。：利用哈希表（HashSet）快速查询元素是否存在，避免重复遍历。，找到其中最长的连续数字序列的长度。要求算法的时间复杂度为。循环向后查找连续的数，直到无法继续。存储所有元素，去除重复值。是某个连续序列的最小值。给定一个未排序的整数数组。遍历哈希表中的每个元素。，哈希表为空，直接返回。解释：最长连续序列是。
vscode 安装 leetcode node.js
03-16
即使完成了 Node.js 的安装，仍可能出现类似 “LeetCode extension needs Node.js installed in environment path” 或者 “command ‘leetcode.toggleLeetCodeCn’ not found” 的错误提示[^3]。这通常是因为 ...
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值