二叉树---遍历

二叉树的广度优先遍历、深度优先遍历的递归和非递归实现方式

先序、中序、后序遍历

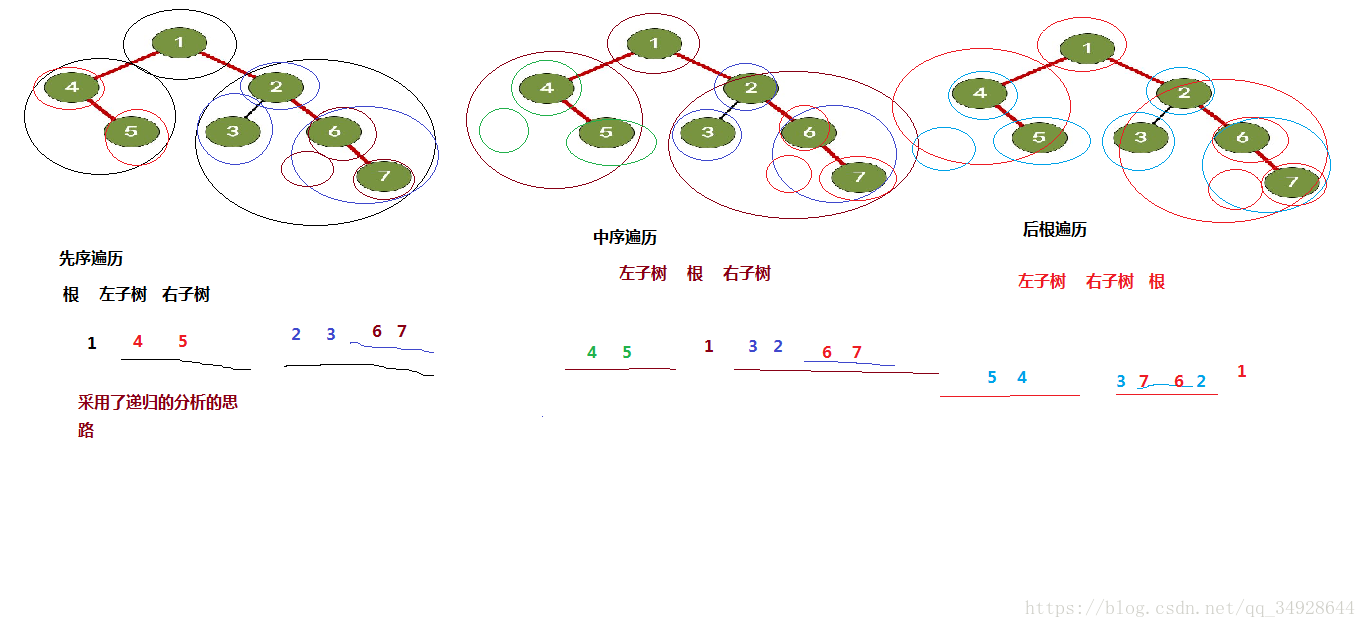
代码演示：

二叉树接口：

package cn.hncu.dataStructure.binTree;
/**
 * 二叉树接口
 * 可以有不同的实现类，每个类可以使用不同的存储结构，比如顺序结构、链式结构
 *
 */
public interface BinaryTree {
	/**
	 * 是否空树
	 * @return
	 */
	public boolean isEmpty();
	/**
	 * 树结点数量
	 * @return
	 */
	public int size();
	
	/**
	 * 获取二叉树的高度
	 * @return
	 */
	public int getHeight();
	/**
	 * 查询指定值的结点
	 * @param value
	 * @return
	 */
	public Node findKey(int value); // 查找
	/**
	 * 前序递归遍历
	 */
	public void preOrderTraverse(); 
	/**
	 * 中序遍历递归操作
	 */
	public void inOrderTraverse();  	
	/**
	 * 后序遍历递归操作
	 */
	public  void postOrderTraverse();
	/**
	 * 中序遍历非递归操作
	 * 1）对于任意节点current，若该节点不为空则将该节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 * 2）若左子树为空，栈顶节点出栈，访问节点后将该节点的右子树置为current
	 * 3) 重复1、2步操作，直到current为空且栈内节点为空。 
	 */
	public void inOrderByStack();
	/**
	 *   前序遍历非递归操作
	 *   1）对于任意节点current，若该节点不为空则访问该节点后再将节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 *   2）若左子树为空，栈顶节点出栈，将该节点的右子树置为current 
	 *   3) 重复1、2步操作，直到current为空且栈内节点为空。
	 */
	public  void preOrderByStack(); 
	/**
	 * 后序遍历非递归操作
	 * 1）对于任意节点current，若该节点不为空则访问该节点后再将节点压栈，并将左子树节点置为current，重复此操作，直到current为空。 
	 * 2）若左子树为空，取栈顶节点的右子树，如果右子树为空或右子树刚访问过，则访问该节点，并将preNode置为该节点 
	 * 3) 重复1、2步操作，直到current为空且栈内节点为空。 
	 */
	public  void postOrderByStack(); 
	
	/**
	 * 按照层次遍历二叉树
	 */
	public void levelOrderByQueue();
}

二叉树节点：

package cn.hncu.dataStructure.binTree;

import java.io.Serializable;

@SuppressWarnings("serial")
public class Node implements Serializable {
	
	private Object value;
	private Node leftChild;
	private Node rightChild;
	
	public Node() {
	}
	
	public Node(Object value, Node leftChild, Node rightChild) {
		this.value = value;
		this.leftChild = leftChild;
		this.rightChild = rightChild;
	}

	public Node(Object value) {
		this.value = value;
	}

	public Object getValue() {
		return value;
	}

	public void setValue(Object value) {
		this.value = value;
	}

	public Node getLeftChild() {
		return leftChild;
	}

	public void setLeftChild(Node leftChild) {
		this.leftChild = leftChild;
	}

	public Node getRightChild() {
		return rightChild;
	}

	public void setRightChild(Node rightChild) {
		this.rightChild = rightChild;
	}

	@Override
	public String toString() {
		return "Node [value=" + value + ", leftChild=" + leftChild + ", rightChild=" + rightChild + "]";
	}
	
}

二叉树接口的实现类：

package cn.hncu.dataStructure.binTree;

import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;

public class LinkedBinaryTree implements BinaryTree {
	
	private Node root; //二叉树的根
	
	public LinkedBinaryTree(Node root) {
		this.root = root;
	}
	public LinkedBinaryTree() {
	}
	
	

	@Override
	public boolean isEmpty() {
		return root == null;
	}

	@Override
	public int size() {
		return size(root);
	}

	private int size(Node node) {
		if( node == null ) {
			return 0;
		}
		//获取左子树的个数
		int leftCount = size(node.getLeftChild());
		
		//获取右子树的个数
		int rightCount = size(node.getRightChild());
		
		return leftCount + rightCount + 1;
	}
	@Override
	public int getHeight() {
		return getHeight(root);
	}
	private int getHeight(Node node) {
		if( node == null ) {
			return 0;
		}
		//获取左子树的高度
		int leftHeight = getHeight(node.getLeftChild());
		//获取右子树的高度
		int rightHeight = getHeight(node.getRightChild());
		//返回最大的高度
		return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
	}

	@Override
	public Node findKey(int value) {
		return findKey(value, root);
	}
	private Node findKey(Object value,Node node) {
		//如果当前节点为空就返回空
		if( node == null ) {
			return null;
		}
		//如果当前节点就是要找的值就返回
		if(node.getValue() != null && node.getValue() == value) {
			return node;
		}
		//当前节点不是要找的值，继续找孩子节点
		Node node1 = findKey(value,node.getLeftChild());
		if(node1 != null && node1.getValue() == value ) {
			return node1;
		}
		Node node2 = findKey(value,node.getRightChild());
		if(node2 != null && node2.getValue() == value ) {
			return node2;
		}
		return null;
	}
	
	@Override
	public void preOrderTraverse() {
		StringBuilder sb = new StringBuilder();
		preOrderTraverse(sb,root);
		
		String strPreOrder = sb.toString();
		//剪去多余的一个','号
		strPreOrder = strPreOrder.substring(0, strPreOrder.length()-1);
		
		System.out.println("先序遍历："+ strPreOrder );
	}
	private void preOrderTraverse(StringBuilder sb, Node node) {
		if(node != null ) {
			
			sb.append(node.getValue()+",");
			
			//2. 把左孩子当作以左孩子为根的树进行先序遍历
			Node leftChild = node.getLeftChild();
			preOrderTraverse(sb,leftChild);
			
			//3. 把右孩子当作以右孩子为根的树进行先序遍历
			Node rightChild = node.getRightChild();
			preOrderTraverse(sb,rightChild);
		}
		
	}
	
	@Override
	public void inOrderTraverse() {
		StringBuilder sb = new StringBuilder();
		inOrderTraverse(sb,root);
		String strPreOrder = sb.toString();
		if(sb.length()>1)
			strPreOrder = strPreOrder.substring(0, strPreOrder.length()-1);
		System.out.println("中序遍历："+ strPreOrder );
	}
	private void inOrderTraverse(StringBuilder sb, Node node) {
		if(node != null ) {
			//1. 把左孩子当作以左孩子为根的树进行中序遍历
			Node leftChild = node.getLeftChild();
			inOrderTraverse(sb,leftChild);
			//2. 把值存起来
			sb.append(node.getValue()+",");
			//3. 把右孩子当作以右孩子为根的树进行中序遍历
			Node rightChild = node.getRightChild();
			inOrderTraverse(sb,rightChild);
		}
	}
	
	@Override
	public void postOrderTraverse() {
		StringBuilder sb = new StringBuilder();
		postOrderTraverse(sb,root);
		String strPreOrder = sb.toString();
		if(sb.length()>1)
			strPreOrder = strPreOrder.substring(0, strPreOrder.length()-1);
		System.out.println("后序遍历："+ strPreOrder );
	}
	private void postOrderTraverse(StringBuilder sb, Node node) {
		if(node != null) {
			//1. 把左孩子当作以左孩子为根的树进行后序遍历
			Node leftChild = node.getLeftChild();
			postOrderTraverse(sb,leftChild);
			//3. 把右孩子当作以右孩子为根的树进行后序遍历
			Node rightChild = node.getRightChild();
			postOrderTraverse(sb,rightChild);
			//2. 把值存起来
			sb.append(node.getValue()+",");
		}
	}

	@Override
	public void inOrderByStack() {
		System.out.print("中序遍历非递归（借助栈）: ");
		StringBuilder sb = new StringBuilder("");
		inOrderByStack(sb,root);
		if(sb.length()>1)
			System.out.println(sb.toString().substring(0, sb.length()-1));
	}
	private void inOrderByStack(StringBuilder sb, Node root) {
		Stack<Node> stack = new Stack<Node>();
		Node node = root;
		while(node != null || !stack.isEmpty() ) {
			//把当前节点的左侧节点全部压到栈中
			while(node != null) {
				stack.push(node);
				node = node.getLeftChild();
			}
			//访问节点，处理改节点的右子树
			if( !stack.empty() ) {
				node = stack.pop();
				sb.append(node.getValue()+",");
				node = node.getRightChild();
			}
		}
		
	}
	
	@Override
	public void preOrderByStack() {
		System.out.print("先序遍历非递归（借助栈）: ");
		StringBuilder sb = new StringBuilder();
		preOrderByStack(sb,root);
		if(sb.length()>1)
			System.out.println(sb.toString().substring(0,sb.length()-1));
	}
	private void preOrderByStack(StringBuilder sb, Node root) {
		Node node = root;
		if( node == null ) return;
		Stack<Node> stack = new Stack<Node>();
		//把根压入栈
		stack.push(node);
		while( !stack.isEmpty() ) {
			//先序，即弹出根节点，表示先访问了
			node = stack.pop();
			sb.append( node.getValue() + "," );
			//接下来判断右子树是否为空，如果不为空就先压入栈
			if(node.getRightChild() != null)
				stack.push( node.getRightChild() );
			//再判断左子树是否为空，如果为空也压入栈
			if(	node.getLeftChild() != null	)
				stack.push( node.getLeftChild() );
			//因为栈：后进先出，所以：先压右，再压左
		}
	}
	
	@Override
	public void postOrderByStack() {
		System.out.print("后序遍历非递归（借助栈）: ");
		StringBuilder sb = new StringBuilder();
		postOrderByStack(sb,root);
		if(sb.length()>1)
			System.out.println(sb.toString().substring(0,sb.length()-1));
	}
	private void postOrderByStack(StringBuilder sb, Node root) {
		Node node = root;
		Stack<Node> stack = new Stack<Node>();
		//访问节点时，判断其右子树是否被访问过
		Node preNode = null;
		while( node != null || !stack.isEmpty() ) {
			//把当前节点以及其左侧节点全部压到栈中
			while( node != null ) {
				stack.push(node);
				node = node.getLeftChild();
			}
			//处理右侧子树
			if( !stack.isEmpty() ) {
				Node rightChild = stack.peek().getRightChild();
				/*如果当前节点的右节点为空，或者是右子树已经访问过了的时候
				     就应该把当前节点弹出栈，并且标记当前节点是已经被访问过的
				     
				     否则就把当前节点的右孩子当作子树的根继续循环
				*/
				if( rightChild == null || preNode == rightChild ) {
					node = stack.pop();
					sb.append( node.getValue() + "," );
					preNode = node;
					node = null;
				} else {
					node = rightChild;
				}
			}
		}
	}
	
	@Override
	public void levelOrderByQueue() {
		System.out.print("按层次遍历使用队列：");
		StringBuilder sb = new StringBuilder();
		levelOrderByQueue(sb,root);
		if(sb.length()>1)
			System.out.println(sb.toString().substring(0, sb.length()-1));
		
	}
	private void levelOrderByQueue(StringBuilder sb, Node node) {
		if( node == null )return;
		Queue<Node> queue = new LinkedList<Node>();
		queue.add(node);
		while(!queue.isEmpty()) {
			node = queue.poll();
			sb.append(node.getValue()+",");
			Node leftChild = node.getLeftChild();
			Node rightChild = node.getRightChild();
			if( leftChild != null ) {
				queue.add(leftChild);
			}
			if (rightChild != null) {
				queue.add(rightChild);
			}
		}
	}
}

演示类：

package cn.hncu.dataStructure.binTree;

public class Demo {
	
	public static void main(String[] args) {
		/*
		 * 树结构
		 *		 1
		 *	 4	     2
		 *	   5   3   6
		 *               7
		 * 
		 */
		//创建一个二叉树
		//左子树
		Node node5 = new Node(5);
		Node node4 = new Node(4, null, node5);
		//右子树
		Node node3 = new Node(3);
		//node7节点用于测试树高度 
		Node node7 = null;
		node7 = new Node(7);
		
		Node node6 = new Node(6,null,node7);
		Node node2 = new Node(2,node3,node6);
		
		Node node1 = new Node(1, node4, node2);
		
		BinaryTree binTree = new LinkedBinaryTree(node1);
		
		//判断树是否为空
		System.out.println( "二叉树是否为空："+ binTree.isEmpty() );
		
		//先序遍历
		binTree.preOrderTraverse();
		
		//中序遍历
		binTree.inOrderTraverse();
		
		//后序遍历
		binTree.postOrderTraverse();
		
		//二叉树的高度
		int height = binTree.getHeight();
		System.out.println("二叉树的高度：" + height );
		
		//二叉树的节点数
		int count = binTree.size();
		System.out.println("二叉树的节点数：" + count );
		
		//在二叉树中找某个值
		Node node = binTree.findKey(4);
		System.out.println(node);
		
		//按层次遍历（借助队列）
		binTree.levelOrderByQueue();
		
		//先序序遍历非递归（借助栈）
		binTree.preOrderByStack();
		
		//中序遍历非递归（借助栈）
		binTree.inOrderByStack();
		
		//后序遍历非递归（借助栈）
		binTree.postOrderByStack();
		
	}
}