机器学习（七）逻辑回归之代价函数

机器学习（七）逻辑回归之代价函数

前言：
由机器学习（六）我们得到了二分类问题的假设函数 hθ(x)，那么下一步我们需要确定代价函数 J(θ)，然后通过梯度下降法确定拟合参数θ。

一、代价函数

1、假设函数：

2、对于线性回归的代价函数

3、但是因为 hθ(x)是S型的非线性函数，因此我们得到的J(θ)图形，可能是如下图所示的非凸函数

4、那么对于这样的代价函数J(θ)，我们就很难用梯度下降法得到全局收敛的最小值，我们需要代价函数是凸函数，类似下图所示，这样我们就一定可以通过梯度下降法得到代价函数的全局收敛的最小值。

5、为了解决上面提到的J(θ)是非凸函数的问题，我们寻找其它的数学等价代换，来使得逻辑回归的代价函数为凸函数，
首先，对于代价函数做如下代换：

6、我们观察如下y = -ln(x)和y = -ln(1-x)两个函数的图像

该图像最明显的特性是当x=1时，则y=0；当x=0时，则y趋向于无穷。

该图像最明显的特性是当x=0时，则y=0；当x=1时，y趋向于无穷。
7、对于cost函数，自变量hθ(x⁽ⁱ⁾)∈(0,1)，因变量y⁽ⁱ⁾∈ (0 | 1)，因此，假设
令y=1，则cost(hθ(x⁽ⁱ⁾)，y⁽ⁱ⁾) = -ln(hθ(x⁽ⁱ⁾))
令y=0，则cost(hθ(x⁽ⁱ⁾)，y⁽ⁱ⁾) = -ln(1-hθ(x⁽ⁱ⁾))
则我们分别得到y=0，和y=1图像如下

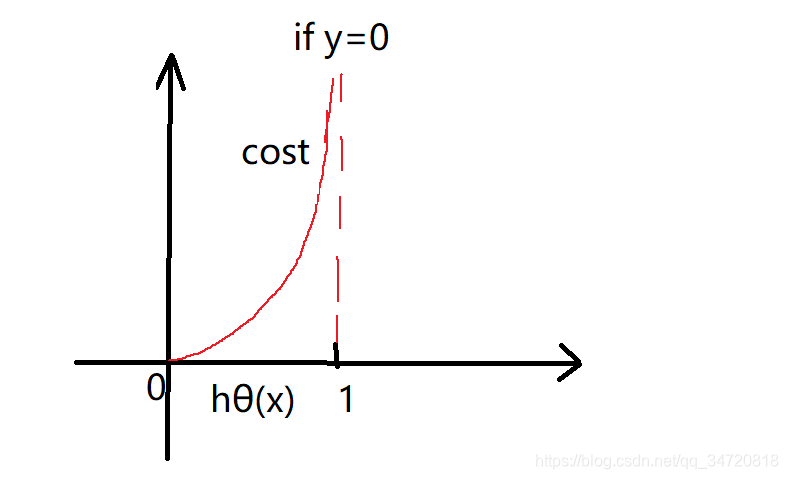
分析这个函数的特征，
if y=0，假设函数hθ(x)=0，代价函数J(θ)=0;
if y=0，假设函数hθ(x)=1，代价函数J(θ)趋向于无穷大；
这不正是我们想要的结果吗？！（因为确定y=0，那么我们希望，当假设函数hθ(x)=0时，代价函数最小，而当假设函数hθ(x)=1时，代价函数最大）

分析这个函数的特征，
if y=1，假设函数hθ(x)=0，代价函数J(θ)趋向于无穷大；
if y=1，假设函数hθ(x)=1，代价函数J(θ)=0；
这不正是我们想要的结果吗？！（因为确定y=1，那么我们希望，当假设函数hθ(x)=1时，代价函数最小，而当假设函数hθ(x)=0时，代价函数最大）

8、对于cost函数，
令y=1，则cost(hθ(x⁽ⁱ⁾)，y⁽ⁱ⁾) = -ln(hθ(x⁽ⁱ⁾))
令y=0，则cost(hθ(x⁽ⁱ⁾)，y⁽ⁱ⁾) = -ln(1-hθ(x⁽ⁱ⁾))
可以整合为一个公式即
cost(hθ(x⁽ⁱ⁾)，y⁽ⁱ⁾) = -yln(hθ(x⁽ⁱ⁾)) - (1-y) ln(1-hθ(x⁽ⁱ⁾))
因此我们得到逻辑回归的代价函数如下：

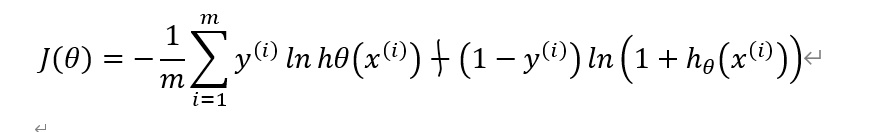
二、逻辑回归之梯度下降法

repeat until constriction
{

note: 一定要同步更新θj，其中 j = 0,1,2,…n
}

代价函数求偏导的推导过程：

注意，虽然逻辑回归的梯度下降法看上去和线性回归一样，但是其中的hθ(x)=1/(1+e^-x)

三、正则化逻辑回归代价函数

四、正确率，召回率，F1值