机器学习（四）梯度下降法之特征缩放、学习速率判断与选择

机器学习（四）梯度下降法之特征缩放、学习速率判断与选择

前言：
由前面梯度下降法的学习可知，如果特征要素对应的样本数据值过大，会使得寻找最小代价函数的“路程”过于坎坷，降低算法效率。针对这种情况我们可以师兄特征缩放方法，一定程度上解决该问题。
同时对于梯度下降法中学习速率，如果选择不当也会造成严重的后果，甚至使得代价函数不能收敛。那么解决这个问题，就需要我们在选择学习速率的同时，实时监控选择的学习速率是否合适，如果发现不合适，应尝试其它选择，那么如何判断选择的学习速率是否合适呢？本文也会讲解。

一、梯度下降法之特征缩放
主要思想是使得所有的特征要素值在一个相对较小的范围之内，使得每个特征要素的样本值近似在-1到1之间

例如：
x₁ 值的范围为0~2000；
x₂ 值的范围在1~5;

对x₁和x₂进行特征缩放如下：
x₁=x₁ / 2000;
x2=x₂ / 5 ;

这样就简单的使得特征缩放到了-1到1的范围之内了，可以提高梯度下降法执行的效率。

对于特征缩放也可以使用平均归一化方法，计算方式如下：

x_i=(x_i- m_i)/s_i；
其中 m_i是训练集中特征要素x_i的平均值，s_i是训练集中特征要素x_i的最大值与最小值之差

二、梯度下降法之学习速率判断与选择

正确的学习速率，会使得代价函数J(θ)随着迭代次数的增加不断趋于收敛状态，如下图趋势为正确的学习速率α

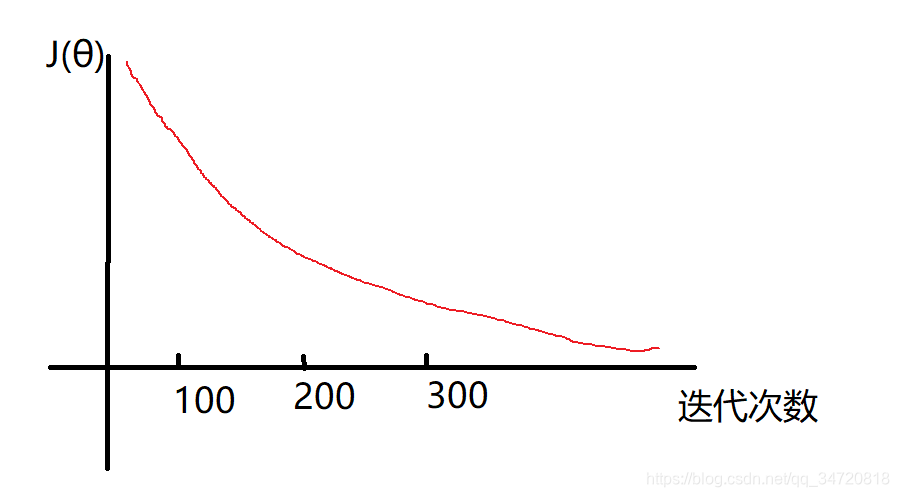
类似如下图的趋势，则表明学习速率α选择的过大，需要适当调小学习速率。

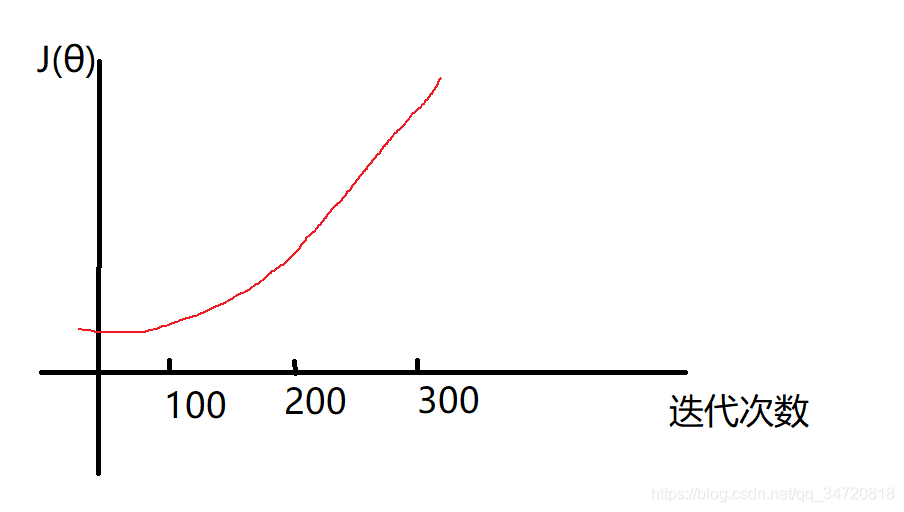
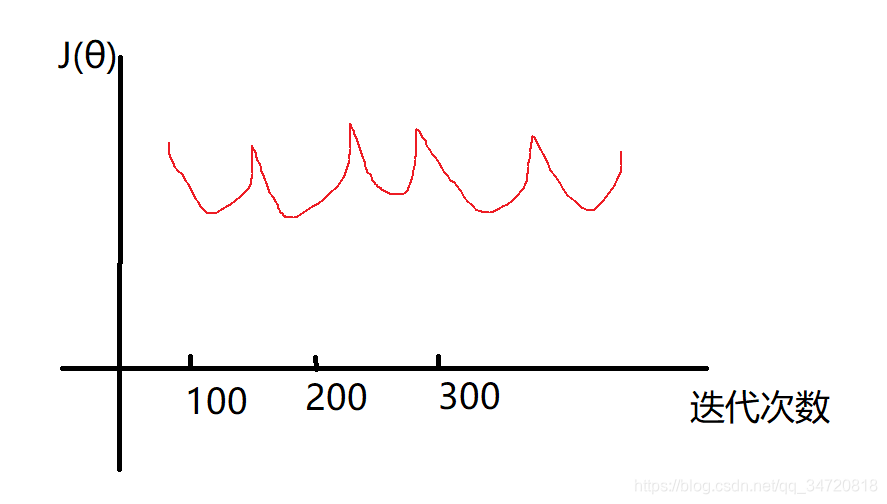
因此如果在算法执行过程中发现J(θ)随着迭代次数的增加并未有收敛趋势，则需要根据图形情况调整学习速率，一般可以类似如下尝试选择学习速率 0.001,0.003,0.01,0.03,1,3,10（大概以倍数进行增加），这只是一种经验，具体使用看情况而定，总之就是不断选择学习速率，然后监视图形是否正常，不断选择优化。