浮点数表示

浮点数的表示

• 浮点数的表示

  • 定点数在字节数固定时，表示范围有限，且我们不能无限制增加字节数

  • 科学计数法

    • eg $3.026\ast 10^{11}$
    • +11 +3.026
    • (阶符)阶码 (数符)尾数
    • 阶码E反映数值大小，使用补码或移码
    • 尾数M部分反映数值精度，使用原码或者补码

  • 当存储空间一定时，不同的存储方式会导致精度不同

    • eg $3.026\ast 10^{11}和0.003\ast 10^{14}$
    • 所以科学计数法会规定，最高有效位不为0，否则会丧失精度
    • 
    • 双符号位可以挽救溢出时的正确符号
    • 

浮点数表征 IEEE 745

• 移码：补码基础上将符号位取反
• 
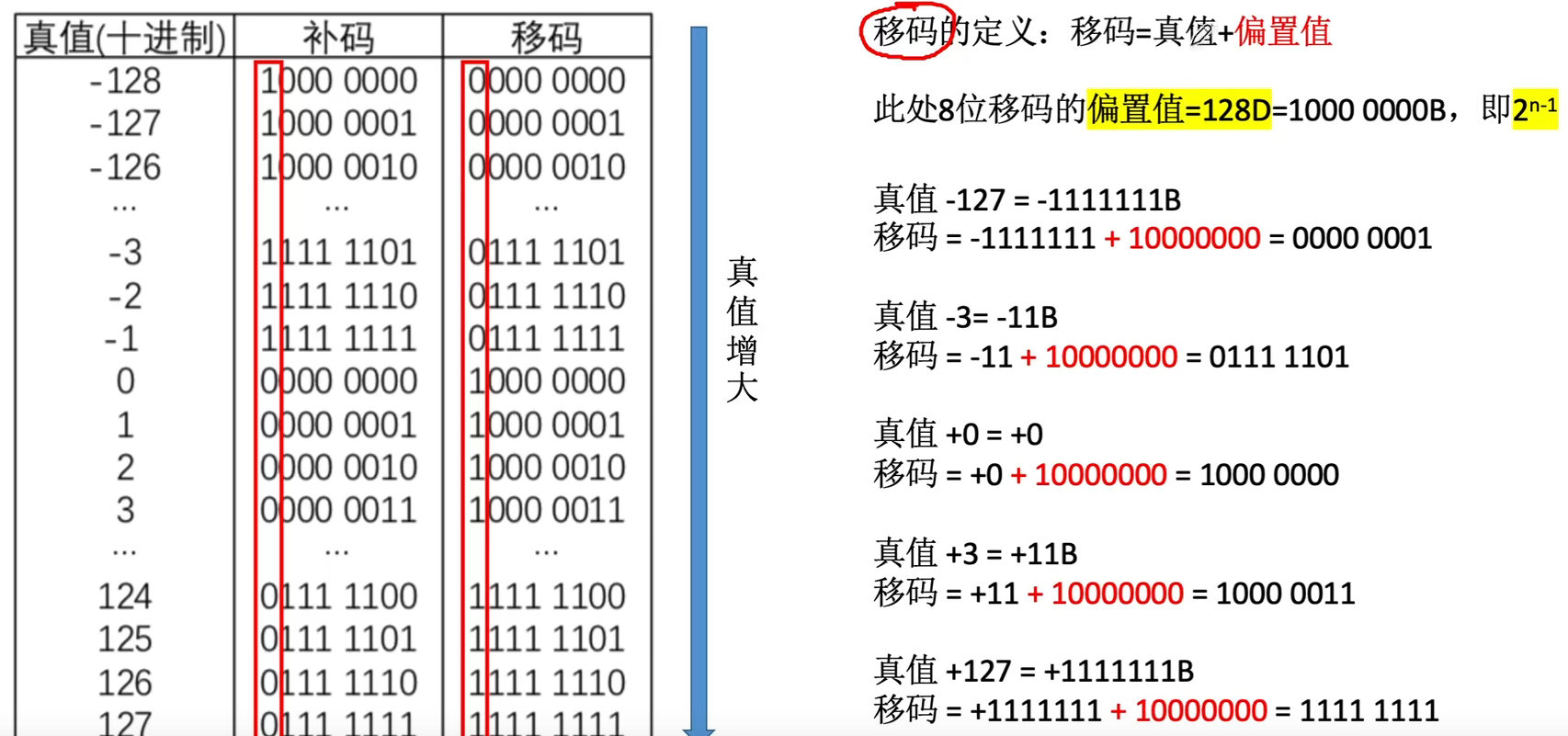
• 754标准，偏置值为$2^n-1$
• 
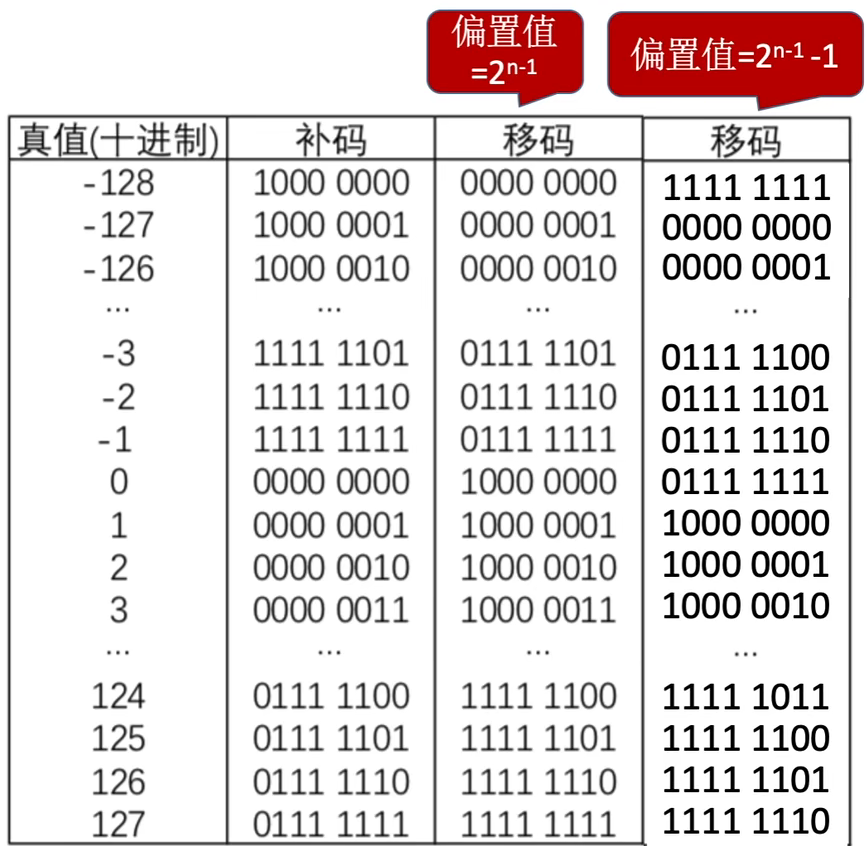
• 754
  • 
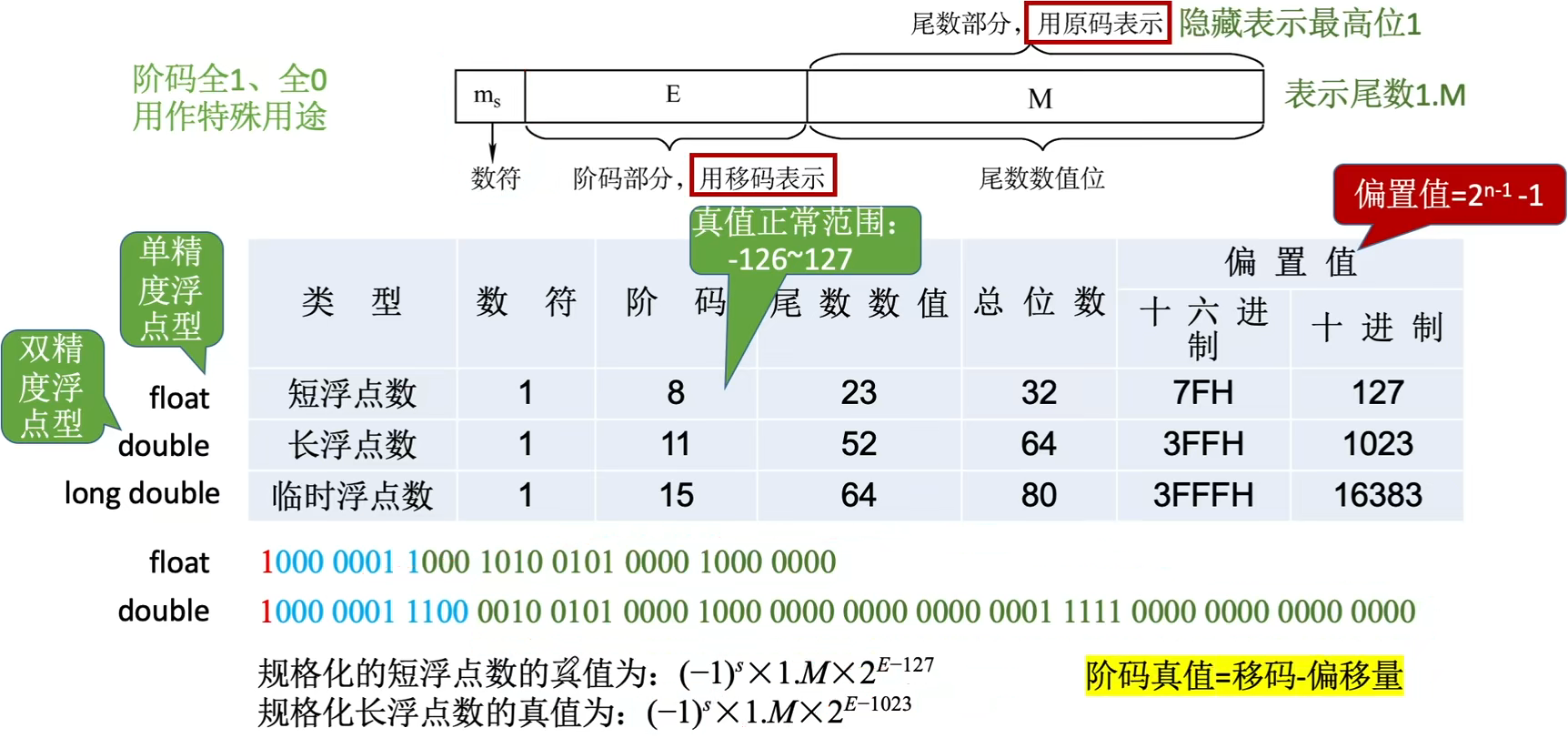
  • 此处因为默认规格化之后，尾数的第一位为1，所以M就设置为23位，尾数为1.M
  • 
  • 在规格化的情况下，最小的真值就是$(1.0{)}_2\ast 2^{-126}$，这是没有问题的；然后肯定还有比这还小的数字，所以此处754用阶码全为0的情况来表示，把精度进一步下探
  • 然后阶码全1时，还可以表示很多内容，从而丰富浮点数的表示