权重更新优化器总结
在上吴恩达的深度学习课程时,学习了很多权重更新的方式,但当时学习的时候比较蒙,可能当时理解了,后面又忘了为什么这么用。这两天又看到一些资料,正好整理总结一下。

我们先计算一下反向传播的公式,具体详细过程就不再讲解了/
以上图为例,现在我们更新权重
w
11
(
2
)
w_{11}^{(2)}
w11(2),更新公式如下所示:
w
11
(
2
)
(
n
e
w
)
=
w
11
(
2
)
(
o
l
d
)
−
l
e
a
r
n
i
n
g
_
r
a
t
e
×
g
r
a
d
i
e
n
t
w_{11}^{(2)}(new) = w_{11}^{(2)}(old) - learning\_rate\times gradient
w11(2)(new)=w11(2)(old)−learning_rate×gradient
在实际训练时数据集的量是非常庞大的,我们不能保证数据一次性全部载入内存,因此只能分批次训练。
如果使用整个样本集进行训练,损失梯度会指向全局最优的方向,如下图所示。

因此在进行梯度传播时我们不能总是保证梯度朝着最优的方向前进。如果使用分批次样本进行求解损失梯度则会指向当前批次最优的方向,但是这个方向从全局来说不一定是最优的方向。如下图所示:

为了解决这个问题我们就要使用到优化器(optimizer),常见的优化器主要有一下几个:
- SGD
- SGD + Momentum
- Adagrad
- RMSProp
- Adam
它们的目的就是为了使网络收敛的更快。
1. SGD优化器(Stochastic Gradient Descent)
SGD也就是我们常说的随机梯度下降方法。
W
t
+
1
=
W
t
−
α
⋅
g
(
W
t
)
W_{t+1} = W_t - \alpha· g(W_t)
Wt+1=Wt−α⋅g(Wt)
缺点:
- 易受样本噪声影响,比如说样本集中有样本的标签标注错误,那么这就会影响梯度下降的方向,可能会使下降方向很大程度上偏离最优方向。
- 可能陷入局部最优解。每一批数据都是随机进行分批次训练,因此在可能存在在某一个批次下其方向与最优方向相背,去了另一个较低点,如下图红线部分所示:

为了解决这个问题,我们就要用到另一个优化方法:SGD + Momentum
2. SGD + Momentum
v
t
=
η
⋅
v
t
−
1
+
α
⋅
g
(
w
t
)
v_t = \eta ·v_{t-1}+\alpha ·g(w_t)
vt=η⋅vt−1+α⋅g(wt)
w
t
+
1
=
w
t
−
v
t
w_{t+1} = w_t - v_t
wt+1=wt−vt其中
α
\alpha
α为学习率,
g
(
w
t
)
g(w_t)
g(wt)为时刻t对参数
w
t
w_t
wt的损失梯度,
η
(
0.9
)
\eta(0.9)
η(0.9)为动量系数。
这么做的意义:

这个方法可以有效抑制样本噪声的干扰。
3. Adagrad
计算公式:
s
t
=
s
t
−
1
+
g
(
w
t
)
⋅
g
(
w
t
)
s_t = s_{t-1} + g(w_t)·g(w_t)
st=st−1+g(wt)⋅g(wt)
w
t
+
1
=
w
t
−
α
s
t
+
ε
⋅
g
(
w
t
)
w_{t+1} = w_t - \frac{\alpha}{\sqrt{s_t+\varepsilon}}·g(w_t)
wt+1=wt−st+εα⋅g(wt)其中
α
\alpha
α为学习率,
g
(
w
t
)
为
t
g(w_t)为t
g(wt)为t时刻对参数
w
t
w_t
wt的损失梯度,
ε
(
1
0
−
7
)
\varepsilon(10^{-7})
ε(10−7)为防止分母为0的小数。
从公式我们可以看出
s
t
s_{t}
st实际上是对前面的梯度求和,这就会使得
s
t
s_{t}
st的值不断增大,在第二个式子中
α
s
t
+
ε
\frac{\alpha}{\sqrt{s_t+\varepsilon}}
st+εα的值会不断减小,就会达到一种学习率自己调节的效果。
但是这样也会出现另一个缺点:刚开始的时候学习率下降的太快,可能还没有收敛就停止了训练。
为了解决这个问题我们可以使用RMSProp优化器(自适应学习率)。
4. RMSProp优化器(自适应学习率)
其实这个优化器就是在Adagrad第一个式子的基础上添加了两个控制因子。
s
t
=
η
⋅
s
t
−
1
+
(
1
−
η
)
⋅
g
(
w
t
)
⋅
g
(
w
t
)
s_t = \eta·s_{t-1} + (1-\eta)·g(w_t)·g(w_t)
st=η⋅st−1+(1−η)⋅g(wt)⋅g(wt)
w
t
+
1
=
w
t
−
α
s
t
+
ε
⋅
g
(
w
t
)
w_{t+1} = w_t - \frac{\alpha}{\sqrt{s_t+\varepsilon}}·g(w_t)
wt+1=wt−st+εα⋅g(wt)其中
α
\alpha
α为学习率,
g
(
w
t
)
为
t
g(w_t)为t
g(wt)为t时刻对参数
w
t
w_t
wt的损失梯度,
ε
(
1
0
−
7
)
\varepsilon(10^{-7})
ε(10−7)为防止分母为0的小数,
η
(
0.9
)
\eta(0.9)
η(0.9)控制衰减速度。
5.Adam优化器(自适应学习率)
计算公式:
m
t
=
β
1
⋅
m
t
−
1
+
(
1
−
β
1
)
⋅
g
(
w
t
)
一
阶
动
量
m_t = \beta_1·m_{t-1} + (1-\beta_1)·g(w_t) \space\space\space\space\space\space\space\space\space\space\space\space\space 一阶动量
mt=β1⋅mt−1+(1−β1)⋅g(wt) 一阶动量
v
t
=
β
2
⋅
v
t
−
1
+
(
1
−
β
2
)
⋅
g
(
w
t
)
⋅
g
(
w
t
)
二
阶
动
量
v_t = \beta_2·v_{t-1} + (1-\beta_2)·g(w_t)·g(w_t) \space\space\space\space\space\space\space\space\space\space\space\space\space 二阶动量
vt=β2⋅vt−1+(1−β2)⋅g(wt)⋅g(wt) 二阶动量
m
t
^
=
m
t
1
−
β
1
t
\hat{m_t} = \frac{m_t}{1-\beta_1^t}
mt^=1−β1tmt
v
t
^
=
v
t
1
−
β
2
t
\hat{v_t} = \frac{v_t}{1-\beta_2^t}
vt^=1−β2tvt
w
t
+
1
=
w
t
−
α
v
t
^
+
ε
m
t
^
w_{t+1} = w_t - \frac{\alpha}{\hat{v_t}+\varepsilon}\hat{m_t}
wt+1=wt−vt^+εαmt^其中
α
\alpha
α为学习率,
g
(
w
t
)
为
t
g(w_t)为t
g(wt)为t时刻对参数
w
t
w_t
wt的损失梯度,
ε
(
1
0
−
7
)
\varepsilon(10^{-7})
ε(10−7)为防止分母为0的小数,
β
1
(
0.9
)
,
β
2
(
0.999
)
\beta_1(0.9),\beta_2(0.999)
β1(0.9),β2(0.999)控制衰减速度。
在实际应用中一般会选择SGD、SGD+Momentum、Adam这几个优化器。
最后附上几个优化器的优化效果。:
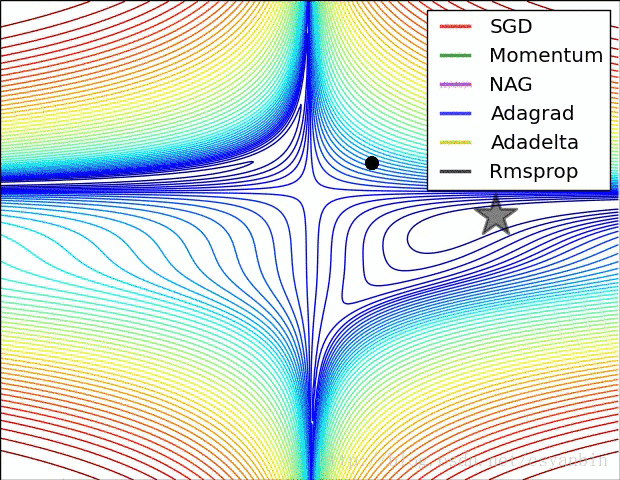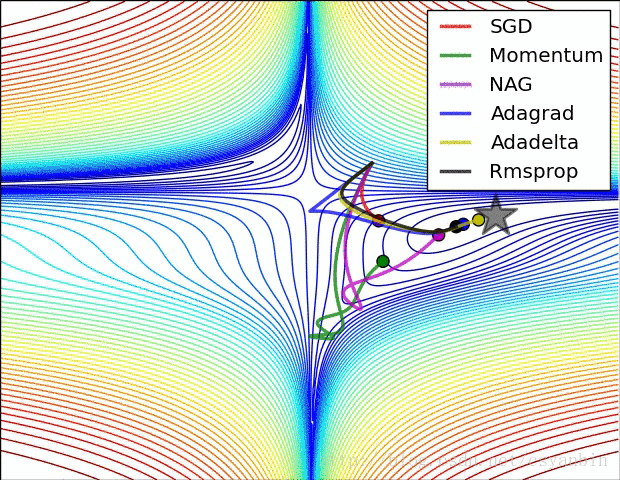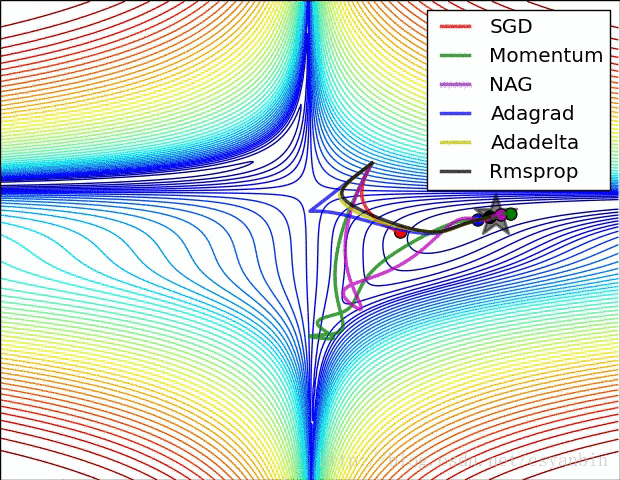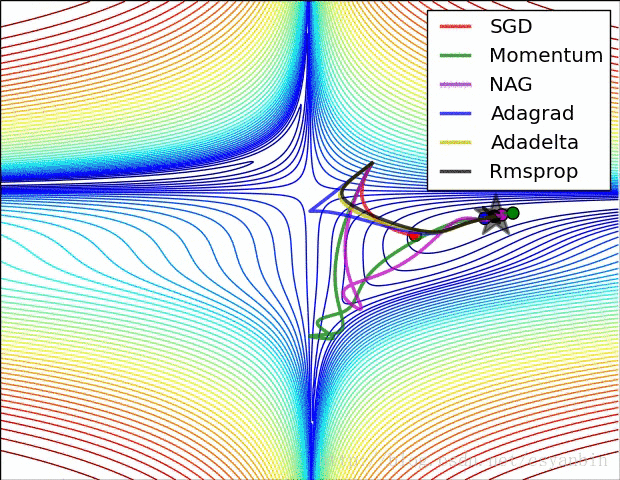
我们可以看出这几个优化器的优化路径和速度,大家可以比较一下。
























 1743
1743

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








