2.1线性表

最新推荐文章于 2025-03-15 10:44:13 发布

草莓酱土司

最新推荐文章于 2025-03-15 10:44:13 发布

阅读量619

点赞数 1

分类专栏：数据结构

本文链接：https://blog.youkuaiyun.com/qq_34554039/article/details/89306540

版权

数据结构专栏收录该内容

4 篇文章

订阅专栏

一、什么是线性表？

1.定义

线性表（Linear List）是由同类型的数据元素构成的有限序列的线性结构。

2.特点

1. 表中元素的个数称为线性表的长度；

2.线性表没有元素时，称为空表；

3.线性表的起始位置称为表头，表结束位置称为表尾；

4.表头没有前驱元素，只有后继元素，表尾只有前驱元素没有后继元素，

除表头、表尾外的中间元素既有前驱元素又有后继元素。

二、线性表的抽象数据类型描述

类型名称：线性表（List）（一般用指针类型）

数据对象集：由n（n≥0)个元素构成的有限序列（ a_1,a_2,a_3,...,a_n )

操作集：线性表L∈List（List为自定义的结构体），整数i表示位置，元素X∈ElementType

线性表的基本操作包括：

1.List MakeEmpty():初始化一个空的线性表L；

2.ElementType FindKth(int K,List L):根据位序K，返回相应的元素；

3.int Find(ElementType X,List L):在线性表L中查找数据X第一次出现的位置；

4.void Insert(ElementType X,int i,List L):在位序i前插入一个新元素X；

5.void Delete(int i,List L):删除指定位序i的元素；

6.int Length(List L):返回线性表L的长度n

（还是之前提到的，对数据的基本操作就是查找、插入、删除，这里多了初始化和求长度）

三、线性表的顺序存储实现（顺序表）

1.特点

利用数组的连续存储空间顺序存放线性表的各元素。

2.顺序表的结构体定义

#define MAXSIZE 20
typedef struct LNode *List;
struct Node
{
    ElementType Data[MAXSIZE];
    int Last;   //Last<=MAXSIZE-1
};
struct LNode L;
List PtrL;

//访问下标为i的元素
L.Data[i];
PtrL->Data[i];

//求线性表的长度
length=L.Last+1;
length=PtrL->Last+1;

这里，需要注意区别数组的程度和线性表的长度

数组的长度：存放线性表的存储空间的长度，即定义中的MAXSIZE，存储分配后，这个量是不变的，之后我们还需要根据这个值来判断线性表是否已满；

线性表的长度：是线性表中数据元素的个数，会随着线性表的插入、删除变化，所以插入、删除操作中，我们要即时更新Last的值，保证线性表的长度可以由Last+1获得。

3.主要操作的实现

（1）初始化，建立空的顺序表

List MakeEmpty()
{
    List PtrL;
    PtrL=(List)malloc(sizeof(struct LNode));
    PtrL->Last=-1;
    return PtrL;
}

(2)查找

int Find(ElementType X,List PtrL)
{
    int i=0;
    while(i<=PtrL->Last &&PtrL->Data[i]!=X)
        i++;
    if(i>PtrL->Last) 
        return -1;  /*没找到，返回-1*/
    else 
        return i;  /*找到了，返回存储位置*/

查找成功的平均比较次数为（n+1)/2，平均时间性能为O(n)

（3）插入

注意两个点：1.第i个位置的数据元素下标为i-1,即在i位置插入应理解为在Data[i-1]插入；

2.倒序向后移动，last->last+1;last-1->last,...,i-1->i，避免数据覆盖。

void Insert(ElementType X,int i,List PtrL)
{
    int j;
    if(PtrL->Last==MAXSIZE-1){ /*表空间已满，不能插入*/
        printf("表满");
        return;
    }
   
    if(i<1||i>PtrL->Last+2){  /*i的取值应该从表头到表尾，即I∈[1,Last+1]*/
        printf("位置不合法");
        return;
    }
    
    for(j=PtrL->Last;j>=i-1;j--)    /*倒序向后移动，将Data[i-1]的位置腾出来*/
        PtrL->Data[j+1]=PtrL->Data[j];    
    PtrL->Data[i-1]=X;        /*插入新元素*/
    PtrL->Last++;        /*Last仍指向最后一个元素*/
    return；
}

平均移动次数为（n+1）/2，平均时间性能为O(n).

4.删除（删除表的第i（ $i\in [1,n]$ ）个位置上的元素）

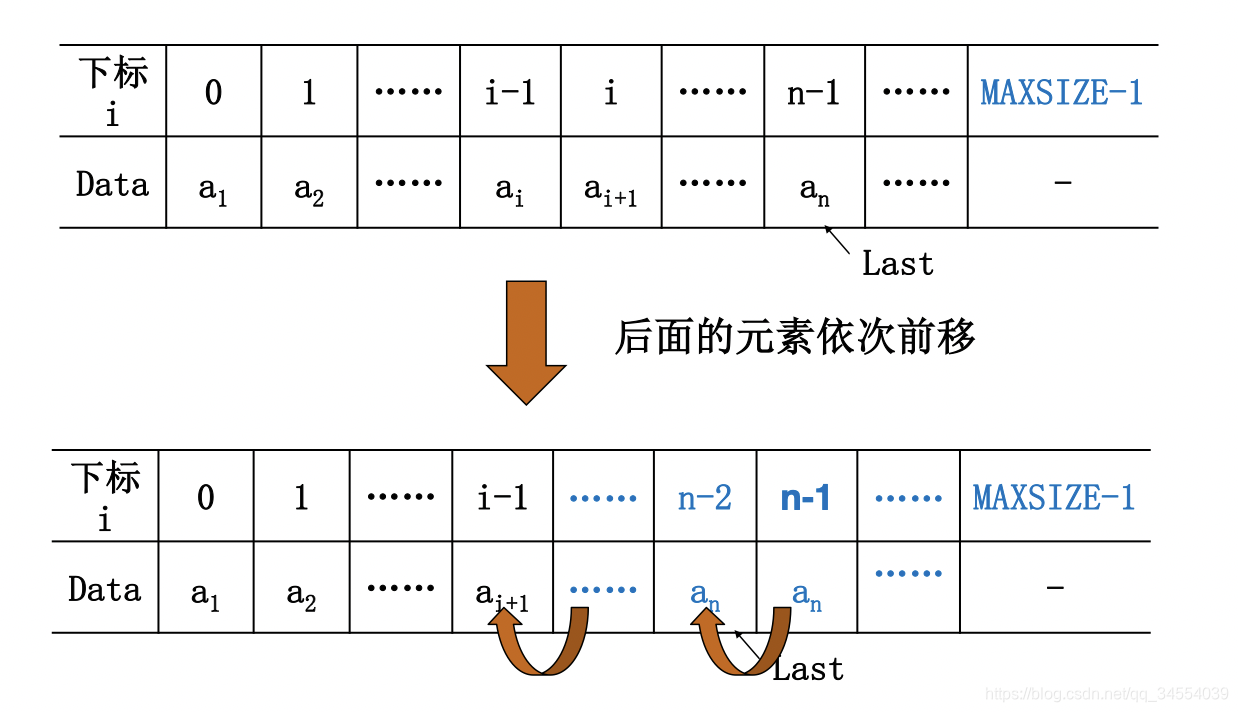
注意：1.还是需要注意位置与下标的区别，位置-1=下标；

2.顺序、向前移动i-1<-i,i<-i+1....,last-1<-last,last=last-1;

void Delete(int I,List PtrL)
{
    int j;
    if(I<1||I>PtrL->last+2){
        printf("不存在第%d个元素",i);
        return;
    }

    for(j=i;j<=PtrL->Last;j++)
        PtrL->Data[j-1]=PtrL->Data[j];
    PtrL->Last--;
    return；
}

平均移动次数为n/2，平均时间性能为O(n).

四、线性表的链式存储实现

1.特点

存储结构分为数据域和指针域两部分，数据域存储该结点的数据元素，指针域存储其后继结点的地址（指针）。

插入、删除操作不需要移动数据元素，只需要修改“链”。（“链”——指针域）
头结点数据域为空，尾结点指针域为空。

定义一个单链表结构体：

typedef struct LNode *List;
struct LNode{
    ElementType Data;
    List Next;
};
struct LNode L;
List PtrL;   /*PtrL为头结点的指针域，即Header，指向表的第一个结点*/

2.主要操作的实现

（1）求表长

时间性能为O(n)。

理解：1.判决条件：指针域为空，说明此时已循环至表尾；

2.p每过一个结点，计数j+1，直到p指向尾结点+1（&（尾结点+1）==NULL）。

int Length(List PtrL)
{
    List p=PtrL;  /*p:第一个结点地址*/
    int j=0;

    while(p){ /*p存放表尾的地址时跳出循环*/       
        p=p->Next;
        j++;
    }
    return j;
}

（2）查找

（2.1）按序号查找 FindKth

平均时间性能为O(n).

//输入：要查找的结点序号K（K=1，2，3，...) 头结点指针PtrL
//输出：第K个结点的指针;没找到则返回NULL。
List FindKth(int K,List PtrL)
{
    List p=PtrL;
    int i=1;
    while(p!=NULL && i<K){
        p=p->Next;
        i++;
    }
    if(i==K) 
        return p;  /*找到第K个结点，返回其指针*/
    else
        return NULL;/*没找到，返回空*/
}

(2.2)按值查找 Find

平均时间性能为O(n).

//输入：要查找的数值X;头结点指针 PtrL
//输出：数值为X的结点的指针
List Find(ElementType X,List PtrL)
{
    List p=PtrL;
    while(p!=NULL && p->Data!=X)
        p=p->Next;
    return p;
}

（3）插入（在第i-1（ $1\leqslant i\leqslant n$ ）个结点后插入一个值为X的新结点）

先构造一个新结点，用s指向；
再找到链表的第i-1个结点，用p指向；
修改指针，插入结点

平均时间性能为O(n).

//输入：要插入的结点的数据X和位置i，表头指针PtrL
//输出：如果插在表头，返回新结点的指针；
//     如果插入位置不合理，返回NULL；
//     否则，返回表头指针PtrL.
List Insert(Elementtype X, int i,List PtrL)
{
    List s,p;
    if(I==1){     /*新结点插入在表头*/
        s=(List)malloc(sizeof(struct LNode));
        s->Data=X;
        s->Next=PtrL;
        return s;
    }
    p=FindKth(i-1,PtrL);  /*查找第i-1个结点*/
    if(p==NULL){  /*第i-1个结点不存在*/
        printf("参数I错误！");
        return NULL;
    }
    else{
        s=(List)malloc(sizeof(struct LNode));
        s->Data=X;
        s->Next=p->Next;
        p->Next=s;
        return PtrL;
    } 
}

（4）删除（删除链表第i（ $1\leqslant i\leqslant n$ ）个位置上的结点）

先找到第i-1个结点，用p指向；
再用指针s指向要被删除的结点（p的下一个结点）；
修改指针，删除s所指向的结点；
最后释放指针，删除s所指结点的空间。

平均查找时间为n/2，平均时间性能为O(n).

List Delete(int i,List PtrL)
{
    List p,s;
    if(i==1){
        s=PtrL;
        if(PtrL!=NULL)
            PtrL=PtrL->Next;
        else
            return NULL;
        free(s);
        return PtrL;
    }
    p=FindKth(i-1,PtrL);
    if(p==NULL)「
        printf("第%d个结点不存在",i-1);
        return NULL;
    }
    else if(p->Next==NULL)
        printf("第%d个结点不存在",i);
    else {
        s=p->Next;
        p->Next=s->Next;
        free(s);
        return PtrL;
    }
}

五、广义表

1.特点

广义表是线性表的推广；
在线性表中，n个元素都是基本的单元素；
而在广义表中，元素不仅可以是单元素，也可以是另一个广义表。

2.广义表的结构体定义

typedef struct GNode *GList;
struct GNode{
    int Tag;   /*标志域：0表示结点为单元素，1表示结点是广义表*/
    union{     /*子表指针域SubList与单元素数据域Data复用，即共用存储空间*/
        ElementType Data;
        GList SubList;
    }URegion;
    GList Next; /*指向后继结点*/
};