计算广告（八）

GBDT

DT－Decision Tree决策树，GB是Gradient Boosting，是一种学习策略，GBDT的含义就是用Gradient Boosting的策略训练出来的DT模型。模型的结果是一组回归分类树组合(CART Tree Ensemble)：T1,T2, ......, Tn 。其中 Tj学习的是之前 j-1棵树预测结果的残差，这种思想就像准备考试前的复习，先做一遍习题册，然后把做错的题目挑出来，在做一次，然后把做错的题目挑出来在做一次，经过反复多轮训练，取得最好的成绩，GBDT学习的是困难样本，更关注哪些分错的样本

而模型最后的输出，是一个样本在各个树中输出的结果的和：

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

GBDT（梯度提升决策树，Gradient Boosting Decision Tree）是一种广泛应用于机器学习的集成算法。其基本原理是通过将多个简单的基学习器（通常是决策树）组合起来，形成一个强大的整体预测模型。GBDT 采用加法模型和前向分布算法，并利用梯度提升方法对基学习器进行优化。

GBDT 的工作过程如下：

初始化：给定训练集 {x_i, y_i}，i=1, 2, ..., n，初始化模型为一个常数值，其值为训练集标签的平均值，即 f_0(x) = avg(y_i)。

迭代：对于每一轮迭代 m（m=1, 2, ..., M），进行以下操作：

1. 计算负梯度：计算每个样本点的负梯度，作为新的目标值。负梯度是损失函数相对于当前模型输出的导数，可以将负梯度视为当前模型预测误差的一种表达。对于平方损失函数（squared loss function），负梯度即为残差（实际值与预测值之差）。

2. 构建新决策树：针对计算出的负梯度，构建新的决策树模型。这个决策树将尝试拟合上一步计算出的负梯度，以最小化损失函数。

3. 计算叶节点权重：为了进一步降低损失函数，需要在新的决策树上计算每个叶节点的权重。

4. 更新模型：将新的决策树乘以学习率（learning rate，一个小于 1 的正数）加入到当前模型中，得到更新后的模型：

f_m(x) = f_{m-1}(x) + learning_rate * new_tree(x)

通过这种方式，每一轮迭代都会逐步减小训练集上的预测误差，并不断优化模型的性能。学习率是一个重要的超参数，用于控制每个基学习器在整体模型中的贡献。较小的学习率可以使模型更稳定，但可能需要更多的迭代次数才能达到理想的性能。

结束条件：迭代过程将在达到预设的最大迭代次数 M 或者训练误差已经足够小时终止。完成迭代后，我们得到了最终的 GBDT 模型：

f(x) = f_0(x) + learning_rate * ∑_{m=1}^M new_tree_m(x)

GBDT 的优点包括：

1自动处理非线性特征和相互依赖关系，具有较强的拟合能力。

2可以处理缺失值和异常值，对数据的分布和比例不敏感。（选择合适的损失函数）

3模型可解释性较强，可以通过特征重要性度量来解释模型的预测行为。

4通过调整超参数（如树的深度、学习率和迭代次数），可以在偏差-方差权衡中找到适当的平衡，提高模型的泛化能力。

然而，GBDT 也存在一些缺点：

1训练过程需要串行迭代，因此训练速度较慢，不易并行化。尽管有一些并行实现方法（如特征并行和数据并行），但它们通常无法完全解决训练速度问题。

对于高维稀疏数据，GBDT 的效果可能不如线性模型。

2在某些情况下，GBDT 容易过拟合，特别是在数据量较小或者噪声较大的情况下。

尽管存在这些局限性，GBDT 仍然是一种在许多机器学习任务中表现优秀的算法。例如，它在回归、分类以及排序等任务中均取得了显著的成功。此外，GBDT 在许多 Kaggle 竞赛中也被证明是非常有效的方法。

为了克服 GBDT 的部分局限性，一些改进和变体方法被提出，如 XGBoost（Extreme Gradient Boosting）、LightGBM 和 CatBoost 等。这些算法在 GBDT 的基础上进行了优化，以提高训练速度、减少内存占用以及提高模型的准确性。

例如，

1. XGBoost 采用了更高效的正则化策略、特征选择和列块压缩技术，以提高训练速度和防止过拟合。

2. LightGBM 则引入了基于梯度的单边采样（GOSS）和互斥特征捆绑（EFB）等方法，进一步提高了训练效率。

3. CatBoost 则专注于处理类别特征，并采用了一种特殊的目标编码策略，以减少类别特征引入的噪声。

总之，GBDT 是一种强大的集成学习方法，在许多实际应用场景中取得了显著的成功。通过结合多个简单的基学习器（通常为决策树），GBDT 利用梯度提升技术逐步优化模型性能。尽管其训练过程可能相对较慢，但 GBDT 的优势在于其强大的拟合能力、对非线性关系和相互依赖特征的处理、以及较好的可解释性。为了克服 GBDT 的部分缺点，许多改进和变体方法也应运而生，如 XGBoost、LightGBM 和 CatBoost 等，进一步提高了训练速度和模型的准确性。这些算法的广泛应用和成功案例充分展示了 GBDT 及其衍生算法在各种机器学习任务中的重要地位。

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

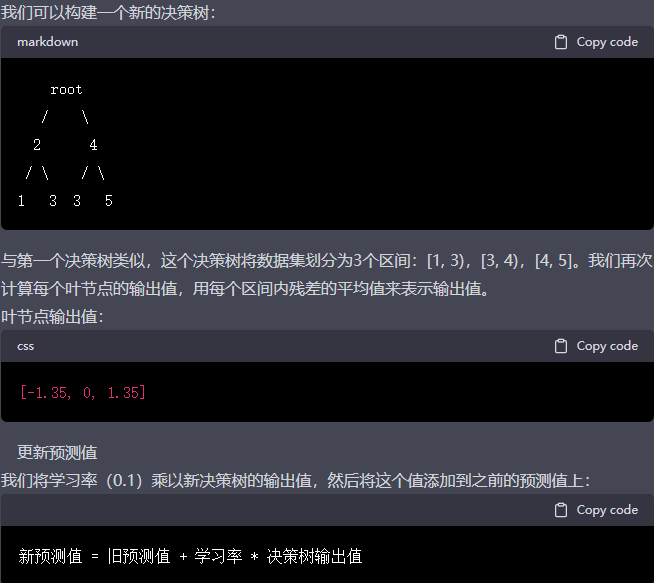
编辑切换为居中

添加图片注释，不超过 140 字（可选）

1: 2.85 + 0.1 * (-1.35) = 2.715

2: 2.85 + 0.1 * (-1.35)= 2.715

3: 3 + 0.1 * (0) = 3

4: 3.15 + 0.1 * (1.35) = 3.285

5: 3.15 + 0.1 * (1.35) = 3.285

预测: 2.715 2.715 3 3.285 3.285

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

算法步骤解释：

初始化，估计使损失函数极小化的常数值，它是只有一个根节点的树，即ganma是一个常数值。

循环构建树

计算损失函数的负梯度在当前模型的值，将它作为残差的估计

估计回归树叶节点区域，以拟合残差的近似值

利用线性搜索估计叶节点区域的值，使损失函数极小化

更新回归树

得到输出的最终模型 f(x)

​

编辑切换为居中

添加图片注释，不超过 140 字（可选）

我们需要通过用第m-1轮残差的均值来得到函数fm（ｘ），进而优化函数Fm（ｘ）。而回归树的原理就是通过最佳划分区域的均值来进行预测。所以fm（ｘ）可以选用回归树作为基础模型，将初始值，m-1颗回归树的预测值相加便可以预测y

GBDT 是一种集成学习方法，它通过组合多个弱学习器（通常是决策树）来构建一个更强大的模型。

GBDT 的基本思想是利用梯度下降算法来优化损失函数。每一步迭代，都会训练一个新的弱学习器来拟合之前模型的残差。

Fm(X) 表示第 m 步的模型，fm(x) 表示在第 m 步训练的弱学习器。以下是 GBDT 的迭代公式：

Fm(X) = Fm-1(X) + fm(x)

MSE 是一种衡量回归模型预测性能的指标。损失函数 Loss 定义如下：

Loss = 1/n * sum_n[(yi-yi_hat)^2] = 1/n * (yi - Fm(x))^2

MSE 的损失函数是预测值（yi_hat，这里用 Fm(x) 表示）与实际值（yi）之间差值的平方和的平均值。这里的 n 表示样本数量。损失函数的目标是找到一个模型 Fm(x)，使得损失函数的值最小化。

泰勒公式是一种在给定点附近对函数进行近似的方法。这里提到的泰勒公式展开：

f(x+x0) = f(x) + f'(x)x0

其中，f(x) 是一个可微函数，x0 是一个小的增量。泰勒公式表示，当 x 增加一个小的值 x0 时，f(x+x0) 可以用 f(x) 加上导数 f'(x) 乘以 x0 来近似。

接下来，我们考虑损失函数 Loss 对 Fm(x) 的一阶导数（Loss'）和二阶导数（Loss''）：

Loss' = 2/n *Loss' = 2/n * sum_n[(Fm(x) - yi)]

损失函数的一阶导数表示损失函数 Loss 关于 Fm(x) 的梯度。

通过计算梯度，我们可以知道在优化损失函数时，需要沿着梯度的负方向进行调整。一阶导数值是实际值和预测值之间的差值的和的 2/n 倍。

Loss'' = 2/n * n * 1 = 2

损失函数的二阶导数表示损失函数 Loss 关于 Fm(x) 的曲率。

二阶导数值告诉我们损失函数是凸的还是凹的。在这个例子中，二阶导数是一个常数，等于 2，说明损失函数是凸函数。对于凸函数，我们可以保证梯度下降法收敛到一个全局最优解。

总之，这段话解释了 GBDT 的基本原理、均方误差损失函数，以及损失函数的一阶导数和二阶导数。通过优这些导数，我们可以应用梯度下降算法来训练 GBDT。在每次迭代过程中，我们都会训练一个新的弱学习器（通常是决策树），以拟合先前模型的残差。我们会根据损失函数的一阶导数（梯度）来调整模型参数，从而使损失函数最小化。这个过程会持续进行，直到达到预设的迭代次数或满足其他停止条件。

在实践中，GBDT 是一种非常高效且广泛应用的机器学习算法，可以处理各种回归和分类问题。它通过不断地优化损失函数，组合多个弱学习器，以达到较高的预测性能。

import numpy as np
from sklearn import metrics
from sklearn.metrics import r2_score  # R square# MAPE和SMAPE需要自己实现

def mape(y_true, y_pred): return np.mean(np.abs((y_pred - y_true) / y_true)) * 100
def smape(y_true, y_pred): return 2.0 * np.mean(np.abs(y_pred - y_true) / (np.abs(y_pred) + np.abs(y_true))) * 100
y_true = np.array([1.0, 5.0, 4.0, 3.0, 2.0, 5.0, -3.0])
y_pred = np.array([1.0, 4.5, 3.5, 5.0, 8.0, 4.5, 1.0])  # MSE
print(metrics.mean_squared_error(y_true, y_pred))  # 8.107142857142858
# RMSE
print(np.sqrt(metrics.mean_squared_error(y_true, y_pred)))  # 2.847304489713536
# MAE
print(metrics.mean_absolute_error(y_true, y_pred))  # 1.9285714285714286
# MAPE
print(mape(y_true, y_pred))  # 76.07142857142858，即76%
# SMAPE
print(smape(y_true, y_pred))  # 57.76942355889724，即58%
print(r2_score(y_true, y_pred)) #-0.1893712574850297

GBDT回归程序

import torch
from torch import nn
from torch.utils.data import DataLoader, Dataset
from sklearn.datasets import make_regression
from sklearn.model_selection import train_test_split

# 生成自己的数据集
X, y = make_regression(n_samples=1000, n_features=10, noise=0.1, random_state=42)

# 将数据集拆分为训练集和测试集（测试集占20%）