平衡二叉树概念
在保持二叉树的基本原则外,任意结点左右子树高度差绝对值不超过1。
平衡二叉树实现原理
平衡二叉树相较于二叉搜索树会增加一个高度标识,用来标识每个结点的高度height,既而更方便的算出是否符合结点左右子树高度差balance绝对值小于等于1。每当插入一个结点,先检查是否因插入而破坏了树的平衡性,若是,则找出最小不平衡子树,在保持二叉搜索树特性前提下,调整最小不平衡子树中各结点之间的链接关系,进行相应的旋转,使之成为新的平衡子树。
当进行添加,删除或插入操作时,如果平衡因子大于一,则代表其左子树的高度大于右子树,,需要进行右旋转,将该结点旋转到其右结点下的右结点,例如一个数组a[10]={3,2,1,4,5,6,7,10,9,8},默认的二叉搜索树结构为:
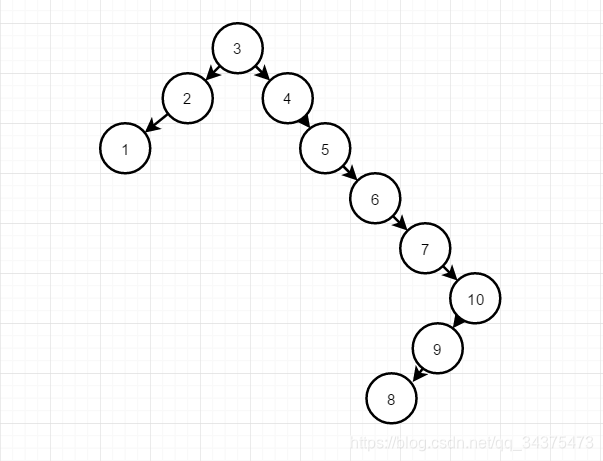
但其不符合平衡二叉树的规则,以根结点为例,其平衡因子绝对值为5,超过了1。
现在按照平衡二叉树的规则进行插入
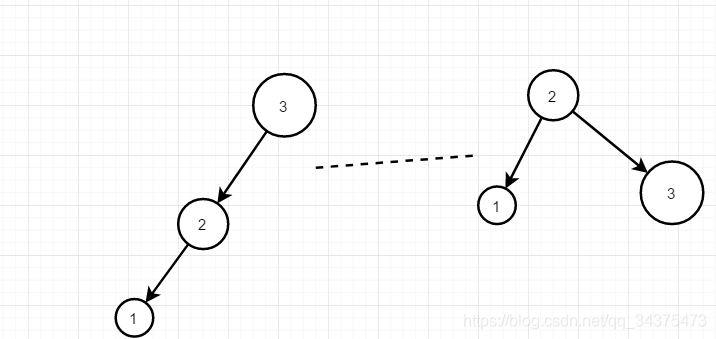
当添加1时,3这个根结点的平衡因子是2,超过了1,所以此时就不平衡了,要进行旋转,因其左结点高度大于右结点,所以进行右旋转。如右图,此时就平衡了。然后继续添加元素,当添加到元素5时,此时二叉树又不平衡了,然后进行旋转调整
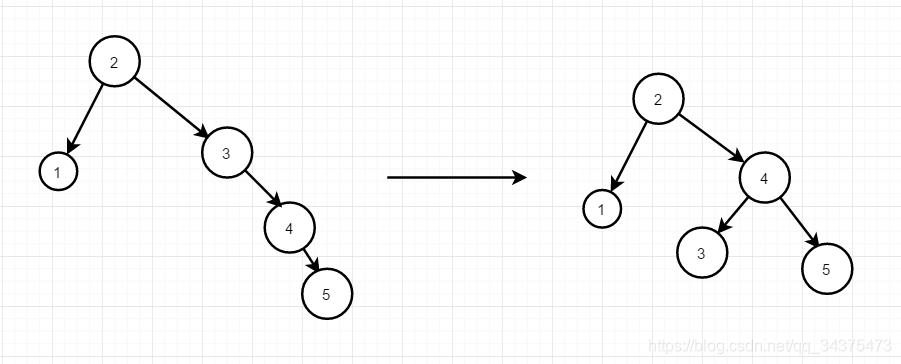
依次类推
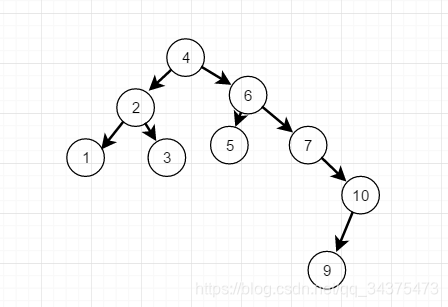
当添加到9时,此时结点7的平衡因子变成了-2,理论上我们只需要旋转最小不平衡子树7,9,10即可,但是如果左旋转后,结点9就成了10的右孩子,这是不符合二叉排序树的特性,此时不能简单的左旋,结点7的平衡因子是-2,结点10平衡因子是1,它们两一正一负,符号不统一,而前面的几次旋转,无论左旋还是右旋,最小不平衡子树的根结点与它的子结点符号都是相同,所以我们首先要做的就是要统一符号,我们先对结点9和结点10进行右旋转,使得结点0成了9的右子树,结点9的平衡因子就成了-1,与7的平衡因子符号相同,这样我们再对结点7进行左旋,如图所示
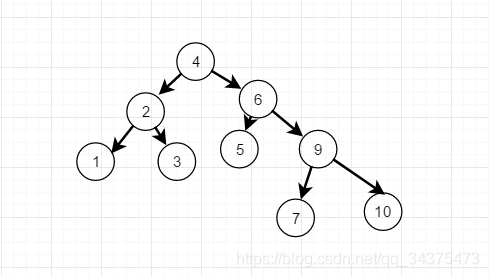
接着插入8,与刚才类似,结点6的平衡因子是-2,而它的右孩子9的平衡因子是1,因此以9为根结点,进行右旋,此时结点6和结点7的符号都是负,再以6为根结点左旋,最终得到最后的平衡二叉树
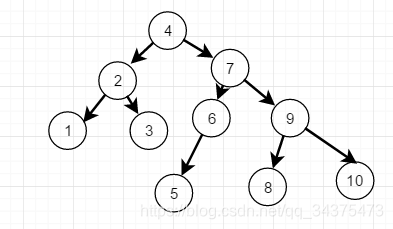
具体代码实现
package AVLTree;
import dataString.NewString;
/**
* Created by lirui on 2018/12/27.
*/
public class AVLTree<K extends Comparable<K>, V> {
private class Node {
private Node left;//左结点
private Node right;//右结点
private int height;//结点高度
private K k;
private V v;
public Node(K k, V v) {
this.k = k;
this.v = v;
left = null;
right = null;
height = 1;
}
}
private int size;
private Node root;
public AVLTree() {
root = null;
size = 0;
}
//长度
public int getSize() {
return size;
}
//判断是否为空
public boolean isEmpty() {
return size == 0;
}
public void add(K k, V v) {
}
private Node add(Node node, K k, V v) {
if (node == null) {
size++;
node = new Node(k, v);
}
if (k.compareTo(node.k) < 0) {
return node.left = add(node.left, k, v);
} else if (k.compareTo(node.k) > 0) {
return node.right = add(node.right, k, v);
} else {
node.v = v;
}
//获取高度
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
//计算平衡因子
int balancer = getBalance(node);
//绝对值大于1不平衡
if (Math.abs(balancer) > 1) {
//平衡因子大于1,右旋转 ,RR
if (balancer > 1 && getBalance(node.left) >= 0) {
return rightRotate(node);
} else//右旋转 RR
if (balancer < -1 && getBalance(node.right) <= 0) {
return leftRotate(node);
} else if (balancer > 1 && getBalance(node.left) < 0) {//平衡因子大于一,其左结点平衡因子小于0,先左旋转,再右旋转
node.left=leftRotate(node.left);
return rightRotate(node);
}else if (balancer<-1&&getBalance(node.right)>0){//平衡因子小于-1,其右结点平衡因子大于0,先右旋转,再左旋转
node.right=rightRotate(node.right);
return leftRotate(node);
}
}
return node;
}
//右旋转
private Node rightRotate(Node node) {
Node x = node.left;
Node tedNode = x.right;
x.right = node;
node.left = tedNode;
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return node;
}
//左旋转
private Node leftRotate(Node node) {
Node x = node.right;
Node tedNode = x.left;
x.left = node;
node.right = tedNode;
node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
x.height = 1 + Math.max(getHeight(x.left), getHeight(x.right));
return node;
}
//获取结点高度
private int getHeight(Node node) {
if (node == null) {
return 0;
}
return node.height;
}
//计算平衡因子
private int getBalance(Node node) {
return getHeight(node.left) - getHeight(node.right);
}
//返回以node为根结点的K所在的结点
private Node getNode(Node node,K k){
if (node==null){
return null;
}
if (k.compareTo(node.k)==0){
return node;
}else if (k.compareTo(node.k)<0){
return getNode(node.left,k);
}else{
return getNode(node.right,k);
}
}
//判断是否包含该结点
public boolean getContains(K k){
return getNode(root,k)!=null;
}
//获取该k的v值
public V getValue(K k){
Node s= getNode(root,k);
return s==null?null:s.v;
}
//修改当前k的v值
public void setValue(K k,V newValue){
Node s=getNode(root,k);
if (s==null){
throw new IllegalArgumentException("is not exist");
}
s.v=newValue;
}
//返回以node为根最小值所在的结点
private Node min(Node node){
if (node.left==null){
return node;
}
return min(node.left);
}
//返回以node为根最大值所在节点
private Node max(Node node){
if (node.right==null){
return node;
}
return max(node.right);
}
//删除某个节点
private Node remove(Node node,K k){
if (node==null){
return null;
}
Node redNode=null;
if (k.compareTo(node.k)<0){
node.left=remove(node.left,k);
redNode=node;
}else if (k.compareTo(node.k)>0){
node.right=remove(node.right,k);
redNode=node;
}else{
if (node.left==null){
Node rightnode=node.right;
node.right=null;
size--;
redNode=rightnode;
}else
if (node.right==null){
Node leftnode=node.left;
node.left=null;
size--;
redNode=leftnode;
}else{
// 待删除节点左右子树均不为空的情况
// 找到比待删除节点大的最小节点, 即待删除节点右子树的最小节点
// 用这个节点顶替待删除节点的位置
Node successor = min(node.right);
successor.right = remove(node.right, successor.k);
successor.left = node.left;
node.left = node.right = null;
redNode = successor;
}
}
if(redNode == null)
return null;
// 更新height
redNode.height = 1 + Math.max(getHeight(redNode.left), getHeight(redNode.right));
// 计算平衡因子
int balanceFactor = getBalance(redNode);
if(Math.abs(balanceFactor) > 1) {
System.out.println("unbalanced : " + balanceFactor);
//如果平衡因子大于一向右旋转
if (balanceFactor>1&&getBalance(redNode.left)>=0){
return rightRotate(redNode);
}
//如果平衡因子小于-1向左旋转
if (balanceFactor<-1&&getBalance(redNode.right)<=0){
return leftRotate(redNode);
}
//LR
if (balanceFactor>1&&getBalance(redNode.left)<0){
redNode.left=leftRotate(redNode.left);
return rightRotate(redNode);
}
//RL
if (balanceFactor<-1&&getBalance(redNode.right)>0){
redNode.right=rightRotate(redNode.right);
return leftRotate(redNode);
}
}
return redNode;
}
public boolean isBalance(){
return isBalance(root);
}
//判断是否是平衡二叉树
private boolean isBalance(Node node){
if (node==null){
return true;
}
int balancer=getBalance(node);
if (Math.abs(balancer)>1){
return false;
}
return isBalance(node.left)&&isBalance(node.right);
}
}

























 353
353

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










