2021-08-20 图排序算法复习_图排序-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_34276797/article/details/119817356

本文详细介绍了两种经典的排序算法——冒泡排序和快速排序，包括它们的时间复杂度、空间复杂度和稳定性。接着，深入探讨了图的基本概念、存储结构和遍历方法，如深度优先遍历和广度优先遍历。此外，还讨论了图的应用，如最小生成树的Prim算法和Kruskal算法，以及求最短路径的Dijkstra算法和Floyd算法。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

图

排序算法复习

冒泡排序


void bubbleSort1(vector<int> &v)
{
                    // 因为n-1个元素排好序了，第n个元素自然就排好序了
    for (int i = 0; i < v.size() - 1; i++)
    {                   // 每次都确定一个最大的元素
        for (int j = 0; j < v.size() - i - 1; j++)
        {       // 如果前一个比后一个大，就交换，循环到已经有序的位置         
            if (v[j] > v[j + 1])
            {
                int temp = v[j];
                v[j] = v[j + 1];
                v[j + 1] = temp;
            }
        }
    }

void bubleSort2(vector<int> &v) 
{
	for(int i = 0; i < v.size() - 1; i++) {
		flag = false;										// 表示本趟冒泡是否发生交换的标志
    for(int j = v.size() - 1; j > i; j--) { // 一趟冒泡过程
			if(v[j-1] > v[j]) {					// 若为逆序
				swap(v[j-1], v[j]);				// 交换
				flag = true;
			}
    }
		if(flag == false) {
				return ;								// 本趟遍历后没有发生交换，说明已经有序
			}
	}
}

时间复杂度：

最好情况：O(n)
平均情况：O(n^2)
最坏情况：O(n^2)

空间复杂度：

O(1)

是否稳定：是

快速排序


int partition(vector<int> &v, int low, int high)
{
    int pivot = v[low];
    while (low < high)
    {
        while (low < high && pivot <= v[high])
            high--;
        v[low] = v[high];
        while (low < high && pivot >= v[low])
            low++;
        v[high] = v[low];
    }
    v[low] = pivot;
    return low;
}
 
void quicksort(vector<int> &v, int low, int high)
{
    if (low < high)
    {
        int pivotpos = partition(v, low, high);
        quicksort(v, low, pivotpos - 1);
        quicksort(v, pivotpos + 1, high);
    }
}

时间复杂度：

最好情况：O(nlogn)
平均情况：O(nlogn)
最坏情况：O(n^2)

空间复杂度：

O(logn)

是否稳定：否

快速排序是所有内部排序算法中平均性能最优的排序算法

分析：

空间效率：由于快速排序是递归的，需要借助一个递归工作栈来保存每一层递归调用的必要信息，其容量应与递归调用的最大深度一致。最好情况下为log(n+1); 最坏情况下，因为要进行n-1次递归调用，所以栈的深度为O(logn)。因而空间复杂度在最坏的情况下为O(n), 平均情况下为O(logn)
时间效率：快速排序的运行时间与划分是否对称有关，而后者又与具体的划分算法有关。快速排序的最坏情况发生在两个区域分别包含n-1个元素和0个元素时，这种最大程度的不对称性发生在每一层递归上，即对应于初始排序表基本有序或基本逆序时，就得到最坏情况下的时间复杂度。
稳定性：在划分算法中，若右端区间存在两个关键字相同，且均小于基准值的记录，则在交换到左端区间后，它们的相对位置会发生变换，即快速排序算法是一个不稳定的排序算法。

图

基本概念：

有向图、无向图
连通图：在无向图中，若从顶点v到顶点w有路径存在，则称v到w是连通的。若图G中任一两个顶点都是连通的，则称图G为连通图，否则称为非连通图。
生成树：连通图的生成树是包含图中全部顶点的一个极小连通子图。（极小连通子图是既要保持图连通，又要使得边数最少的子图。
回路：第一个顶点和最后一个顶点相同的路径称为回路或环

图的存储结构

邻接矩阵法

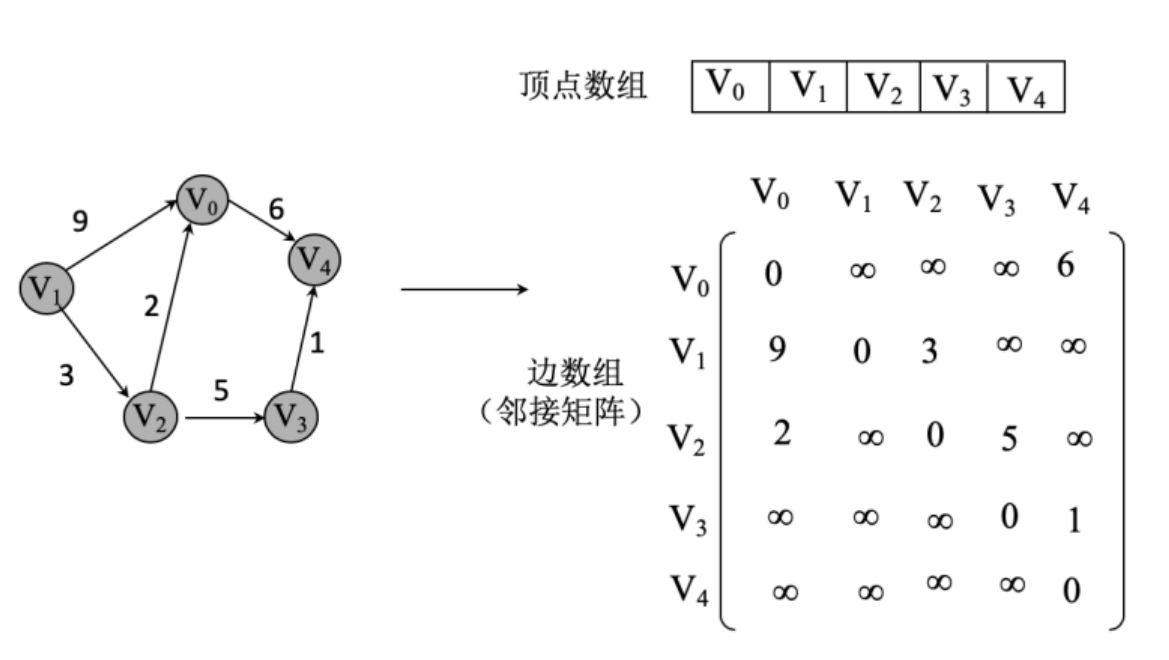
点击查看源网页

设图G的邻接矩阵为A，A^n的元素An[i][j] j 等于由顶点i到顶点j的长度为n的路径的数目。

邻接表法

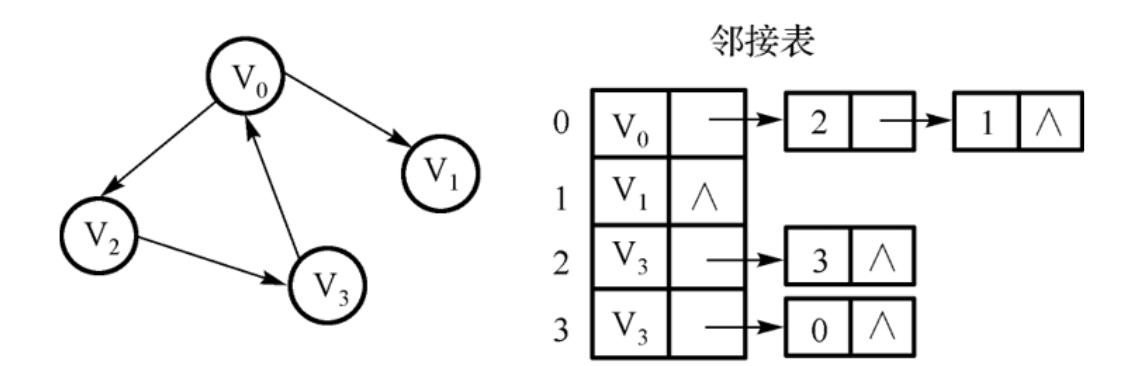
点击查看源网页

图的遍历

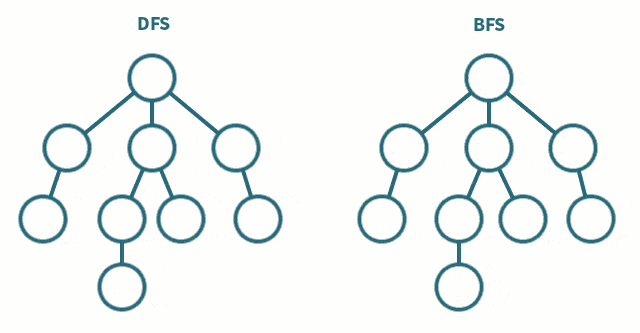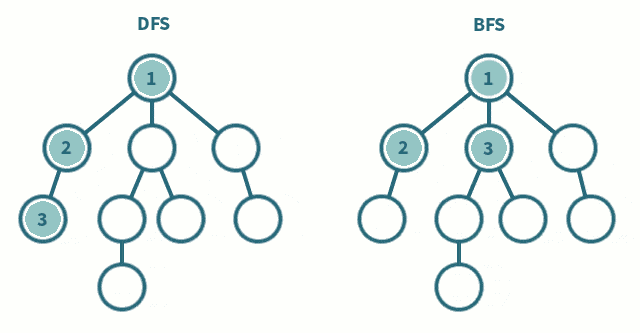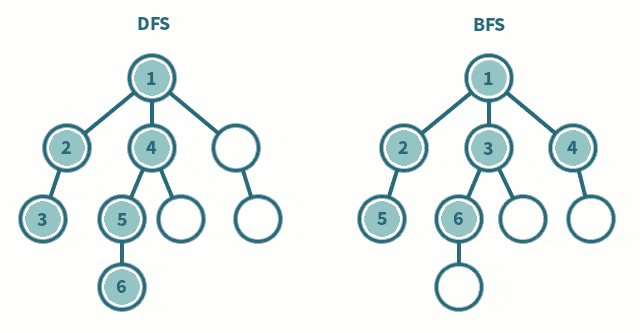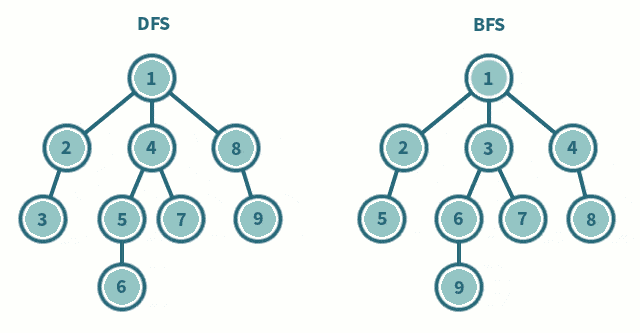
点击查看源网页

深度优先遍历（图的深度优先遍历是二叉树的递归遍历算法的扩展）

void DFSTraverse(Graph G) {
	// 对图G进行深度优先遍历，访问函数为visit()
  for(v=0;v<G.vexnum;++v) {
    visited[v]=false;	// 初始化已访问标记数据
  }
  for(v=0;v<G.vexnum;++v) {
    if(!visited[v]) {
			DFS(G,v);
    }
  }
}

void DFS(Graph G, int v) {
  // 从顶点v出发，采用递归思想，深度优先遍历图G
  visit(v);	//  访问顶点v
  visited[v]=true;	// 设置已访问标记
  for(w = FirstNeighbor(G, v); w>=0; w=NextNeighbor(G,v,w)) 
    if(!visited[w]) {
      DFS(G, w);
    }
}

性能分析：

DFS是一个递归算法，需要借助一个递归工作栈，故它的空间复杂度为O(|V|)。遍历图的过程实质上是对每个顶点查找其邻接点的过程，其耗费的时间取决于所采用的存储结构。当以邻接矩阵表示时，查找每个顶点的邻接点所需时间为O(|V|)，故总的时间复杂度O(|V|^2)，当以邻接表表示时，查找所有顶点的邻接点所需时间为O(|E|)，访问顶点所需时间为O(|V|)，此时的时间复杂度为O(|V| + |E|)。

广度优先遍历（图的广度优先遍历是二叉树的层次遍历算法的扩展）

bool visited[MAX_VERTEX_NUM];	// 访问标记数组

void BFSTraverse(Graph G) {
	// 对图G进行广度优先遍历，设访问函数为visit()
	for(i = 0; i < G.vexnum, ++i) 
		visited[i] = false;				// 访问标记数组初始化
  InitQueue(Q);								// 初始化辅助队列Q
  for(i = 0; i < G.vexnum; ++i) // 从0号顶点开始遍历
    if(!visited[i]) 	// 对每个连通分量调用一次BFS
      BFS(G, i);			// Vi没有访问过，从Vi开始BFS
}

void BFS(Graph G, int v) {
	// 从顶点v出发，广度优先遍历图G，算法借助一个辅助队列Q
  visit(v);				// 访问初始顶点v
  visited[v] = true;	// 对v做已访问标记
  Q.push(v);					// 顶点v入队
  while(!Q.empty()) {
		v = Q.fornt();
    Q.pop();
    for(w = FirstNeighbor(G, v); w>=0; w=NextNeighbor(G,v,w)) // 检查v的所有邻接点
      if(!visited[w]) {	//  w为v的尚未访问的邻接顶点
				visit(w);		// 访问顶点w
        visited[w] = true; 	// 对w做已访问标记
        Q.push(w);			//   顶点w入队
      } // if
  } // while
}

BFS求单源最短路径问题

void BFS_MIN_Distance(Graph G, int u) {
   // d[i] 表示从u到i节点的最短路径
 for(i=0; i<G.vexnum;++i) 
   d[i] = ∞;
 visited[u] = true; d[u] = 0;
 while(!Q.isEmpty()) {
   v = Q.fornt();
   Q.pop();
   for(w = FirstNeighbor(G, v); w>=0; w=NextNeighbor(G,v,w)) 
     if(!visited[w]) {	// w为u的尚未访问的邻接顶点
   			visited[w] = true;
       d[w] = d[u] + 1;
       Q.push(w);
     } // if
 } // while
}

性能分析：

空间复杂度：无论是邻接表还是邻接矩阵的存储方式，BFS算法都会借助一个辅助队列Q，n个顶点均需入队一次，在最坏的情况下，，空间复杂度为O(|V|)。
时间复杂度：但采用邻接表存储方式时，每个顶点均需要搜索一次，故时间复杂度为O(|V|)，在搜索任一顶点的邻接点时，每条边至少访问一次，故时间复杂度为O(|E|)，算法中的时间复杂度为O(|V|+|E|)。当采用邻接矩阵存储方式时，查找每个顶点的邻接点所需时间为O(|V|)，故算法总的时间复杂度为O(|V|^2)。

图的应用

最小生成树：

GENERIC_MST(G) {
	T=NULL;
	while T 未形成一颗生成树;
		do 找到一条最小代价边(u,v) 并加入T后不会产生回路；
			T = T ⋃ (u,v);
}

Prim算法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-jaaZTVJg-1629425649772)(https://tse1-mm.cn.bing.net/th/id/R-C.cabb61105b39a621691355e6ae58fe6e?rik=o5SBCWFSvWZWmw&riu=http%3a%2f%2fwww.lwlwq.com%2fxiaowei%2fhome%2fuploads%2f2015%2f04%2fprim-procedure.png&ehk=aeZzv7VDypK6zgtOB%2faox5cZTFRc08WIQ8DqMSDunVo%3d&risl=&pid=ImgRaw&r=0)]

void Prim(G, T) {
	T=空集； // 初始化空树
	U = {w};	//  添加任一顶点w
	while((V-U) != 空集) {	// 若树中不含全部顶点
		设(u, v)是使u∊U与v∊(V-U),且权值最小的边;
		T=T ⋃ {(u,v)}; // 边归入树
		U=U ⋃ {v};				// 顶点归入树
	}
}

Kruskal算法

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RNGbLNFu-1629425538327)(https://img1.daumcdn.net/thumb/R800x0/?scode=mtistory2&fname=https:%2F%2Ft1.daumcdn.net%2Fcfile%2Ftistory%2F232ACE3F570B903F30)]

void Kruskal(V, T) {
	T = V;	// 初始化树T，仅含顶点
	numS=n;	// 不连通分量数
	while(numS > 1) {		// 如果不连通分量数大于1
		从E中取出权值最小的边(v, u);
		if(v和u属于T中不同的连通分量) {
			T = T ⋃ { (v, u) };	// 将此边加入生成树
			numS--; 	// 不连通分量数减1
		}
	}
}

最短路径：

Dijkstra算法-求单源最短路径问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KR8AbcGq-1629425538329)(/Users/lijian/Downloads/80D1E2658E037B7BFDE6B19063C3D5F5.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V618snSx-1629425538330)(/Users/lijian/Downloads/FEE5BCC11B2C062BE2FAB35FC15B03B4.png)]

从源点到某一个特定顶点的最短路径，时间复杂度为O(|V|^2) ，如果需要找出所有节点对之间的最短距离，则需要对对每个节点运行一次Dijkstra算法，时间复杂度为为O(|V|^3)。

Floyd算法-求各顶点之间最短路径问题

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-UWw9vTk1-1629425538331)(/Users/lijian/Downloads/21AAB7CC55069522A6C68AF8C431A0AE.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-kHoNoKxv-1629425538333)(/Users/lijian/Downloads/824E5372A66FF23E9D630D7D0E6224A1.png)]

时间复杂度为O(|V|^3)

拓扑排序

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XJ4yXk9I-1629425538334)(/Users/lijian/Downloads/FA1BA4B239D9DA530720D801D9897B8C.png)]

bool TopologicalSort(Graph G) {
	// 如果G存在拓扑序列，返回true；否则返回false，这时G中存在环
	InitStack(S);		// 初始化栈
	for(int i=0; i<G.vexnum; i++) {
		if(indegree[i] == 0) {
			Push(S, i);	// 将所有入度为0的顶点进栈
		}
	}
	int count=0;	// 计数，记录当前已经输出的顶点数
	while(!S.empty()) {
		i=S.pop();					// 栈顶元素入栈
		print[count++] = i;	// 输出顶点i
		for(p=G.vertices[i].firstarc; p; p=p->nextarc) {
			// 将所有i指向的顶点的入度减1，并且将入度为0的顶点压入栈S
			v=p->adgvex;
			if(!(--indegree[v])) s.push(v);	// 入度为0, 压入栈
		}
	}
	if(count<G.vexnum) 
		return false;					// 有向图中有回路
	else 
		return true;
}

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GDhuGGlj-1629425657688)(https://tse1-mm.cn.bing.net/th/id/R-C.cabb61105b39a621691355e6ae58fe6e?rik=o5SBCWFSvWZWmw&riu=http%3a%2f%2fwww.lwlwq.com%2fxiaowei%2fhome%2fuploads%2f2015%2f04%2fprim-procedure.png&ehk=aeZzv7VDypK6zgtOB%2faox5cZTFRc08WIQ8DqMSDunVo%3d&risl=&pid=ImgRaw&r=0)]