MATLAB 两椭圆重合面积的填充与计算

最新推荐文章于 2022-12-10 15:14:54 发布
置顶 最新推荐文章于 2022-12-10 15:14:54 发布
阅读量4.5k 收藏 40
点赞数 12
分类专栏： 个人笔记 Matlab 工作杂活 文章标签： matlab 几何学
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_34122861/article/details/121429870
版权
本文介绍如何使用MATLAB实现两椭圆重叠部分的近似填充与面积计算，包括利用交点近似填充及蒙特卡罗方法计算面积。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

0. 前言

使用MATLAB实现两椭圆重合面积的填充与计算。

1. 准备工作

需要提前掌握的知识如下：

  1. MATLAB绘制圆、椭圆、矩形等基本平面图形
    https://blog.youkuaiyun.com/qq_45384561/article/details/104223407
  2. 根据椭圆中心坐标、长半轴、偏心率和方向角画椭圆
    https://blog.youkuaiyun.com/biubiu_buaa/article/details/71081048?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaidudefault-1.essearch_pc_relevant&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaidudefault-1.essearch_pc_relevant
  3. 坐标点的旋转与坐标系的旋转的区别与联系
    https://blog.youkuaiyun.com/qq_39800978/article/details/102698993
  4. 椭圆变换方程（平移+旋转等任意变换）
    https://blog.youkuaiyun.com/qq_41685265/article/details/104267256

2. 两同心椭圆重合面积的近似填充

利用椭圆方程求解得到4个交点，逆时针顺序排序后进行填充。
该填充方式为近似填充，即用四边形近似实际重叠面积。

2.1 代码

% Author: Shaw
% Description: 绘制椭圆交叉面积的函数
% Date: 2021/11/18

function testFill_1118(m,n,A1,B1,phi1,A2,B2,phi2)

    % m:椭圆原点X
    % n:椭圆原点Y

    % A1:椭圆1长轴
    % B1:椭圆1短轴轴
    % phi1:椭圆1绕X轴逆时针旋转角度/°

    % A2:椭圆2长轴
    % B2:椭圆2短轴
    % phi2:椭圆2绕X轴逆时针旋转角度/°

    theta = 0:0.001:2*pi;
    
    % 椭圆参数方程
    xBhat1 =  m + A1 * cos(theta)*cosd(phi1) - B1 * sin(theta) * sind(phi1);
    yBhat1 =  n + A1 * cos(theta)*sind(phi1) + B1 * sin(theta) * cosd(phi1);
    
    xBhat2 =  m + A2 * cos(theta)*cosd(phi2) - B2 * sin(theta) * sind(phi2);
    yBhat2 =  n + A2 * cos(theta)*sind(phi2) + B2 * sin(theta) * cosd(phi2);
    
    % 绘图
    figure
    plot(xBhat1, yBhat1,'r')
    hold on
    plot(xBhat2, yBhat2,'b')
    hold on


    % 求解交点
    syms x y
    
    eq1 = ((x-m)*cosd(phi1) +(y-n)*sind(phi1))^2/A1^2 + (-(x-m)*sind(phi1) +(y-n)*cosd(phi1))^2/B1^2 - 1;
    eq2 = ((x-m)*cosd(phi2) +(y-n)*sind(phi2))^2/A2^2 + (-(x-m)*sind(phi2) +(y-n)*cosd(phi2))^2/B2^2 - 1;


    [xSolve,ySolve]= solve(eq1,eq2);
    
    % 转符号变量为double数
    x0 = double(xSolve);                         
    y0 = double(ySolve);
    
    % 计算交点与椭圆圆心的角度
    thetaCom = atan2d(y0-n,x0-m);

    array = [x0,y0,thetaCom];
    % 依据角度从小到大排列
    % fill指令需要坐标逆时针排序
    arrayProcess = sortrows(array,3);

    % 绘制直线
    line(arrayProcess(:,1),arrayProcess(:,2))
    hold on
    axis equal

    % 填充
    fill(arrayProcess(:,1),arrayProcess(:,2),'g')
end


close all
clear
clc

% m:椭圆原点X
m = 20;
% N:椭圆原点Y
n = 5;

% A1:椭圆1长轴
A1 = 3;
% B1:椭圆1短轴轴
B1 = 1;
% phi1:椭圆1绕X轴逆时针旋转角度/°
phi1 = 45;

% A2:椭圆2长轴
A2 = 5;
% B2:椭圆2短轴
B2 = 2;
% phi2:椭圆2绕X轴逆时针旋转角度/°
phi2 = 120;

testFill_1118(m,n,A1,B1,phi1,A2,B2,phi2)

2.2 近似填充示意图

椭圆的参数见上述代码，绘制的近似填充示意图如下：
在这里插入图片描述

注：
fill函数填充点的坐标顺序必须为逆时针，通过sortrows函数实现各交点与椭圆原点角度的逆时针排序

3. 蒙特卡罗两同心椭圆重合面积的计算及填充

由于近期工作不需要计算重叠面积，所以采用近似的填充方式也可以接受。
如果需要精确计算重叠面积，尤其是不规则图形的重叠面积，则采用蒙特卡罗方法是更好的选择，也能够展现更精确的填充效果！

蒙特卡罗求面积的方法可以理解为：
在比重叠区域面积大的面积为A的区域中随机撒豆子M个，利用重叠面积约束求取所有豆子落在重叠区域上的个数为F，则重叠区域的面积S为

S=A/M*F

“撒豆子”的相关解释可见：
蒙特卡洛算法举例，计算阴影部分面积MATLAB和C语言实现
https://blog.youkuaiyun.com/qq_43530128/article/details/102534301

3.1 代码

% Author: Shaw
% Description: 蒙特卡罗计算椭圆交叉面积，并填充
% Date: 2021/11/20

function area = testMCFill_1120(m,n,A1,B1,phi1,A2,B2,phi2)

    % m:椭圆原点X
    % n:椭圆原点Y

    % A1:椭圆1长轴
    % B1:椭圆1短轴轴
    % phi1:椭圆1绕X轴逆时针旋转角度/°

    % A2:椭圆2长轴
    % B2:椭圆2短轴
    % phi2:椭圆2绕X轴逆时针旋转角度/°
    
    
    theta = 0:0.001:2*pi;

    % 椭圆参数方程
    xBhat1 =  m + A1 * cos(theta)*cosd(phi1) - B1 * sin(theta) * sind(phi1);
    yBhat1 =  n + A1 * cos(theta)*sind(phi1) + B1 * sin(theta) * cosd(phi1);

    xBhat2 =  m + A2 * cos(theta)*cosd(phi2) - B2 * sin(theta) * sind(phi2);
    yBhat2 =  n + A2 * cos(theta)*sind(phi2) + B2 * sin(theta) * cosd(phi2);

    % 绘图
    figure
    plot(xBhat1, yBhat1,'r')
    hold on
    plot(xBhat2, yBhat2,'b')
    hold on
    
    % 计算两椭圆长短轴最大值
    maxLen = max([A1,B1,A2,B2]);
    xmin = m - maxLen;
    ymin = n - maxLen;
    xmax = m + maxLen;
    ymax = n + maxLen;
    
    % 撒豆子个数
    N = 10E7;
    
    % 随机豆子
    xIn = (xmax - xmin) * rand(1,N) + xmin;
    yIn = (ymax - ymin) * rand(1,N) + ymin;
    
    % 椭圆约束
    eqIn1 = ((xIn-m).*cosd(phi1) +(yIn-n).*sind(phi1)).^2/A1^2 + (-(xIn-m).*sind(phi1) +(yIn-n).*cosd(phi1)).^2/B1^2 - 1;
    eqIn2 = ((xIn-m).*cosd(phi2) +(yIn-n).*sind(phi2)).^2/A2^2 + (-(xIn-m).*sind(phi2) +(yIn-n).*cosd(phi2)).^2/B2^2 - 1;
    
    % 在重叠面积内豆子的下标
    index = find(eqIn1<=0 & eqIn2<=0);
    % 重叠面积内豆子的个数
    count = length(index);
    
    % 重叠面积计算
    area = (xmax - xmin) * (ymax - ymin) * count / N;
    
    % 绘制重叠面积
    plot(xIn(index), yIn(index), 'g')
    hold on
    
end

close all
clear
clc

% m:椭圆原点X
m = 20;
% N:椭圆原点Y
n = 5;

% A1:椭圆1长轴
A1 = 3;
% B1:椭圆1短轴轴
B1 = 1;
% phi1:椭圆1绕X轴逆时针旋转角度/°
phi1 = 45;

% A2:椭圆2长轴
A2 = 5;
% B2:椭圆2短轴
B2 = 2;
% phi2:椭圆2绕X轴逆时针旋转角度/°
phi2 = 120;


AREA = testMCFill_1120(m,n,A1,B1,phi1,A2,B2,phi2)

3.2 填充示意图

为方便对比，椭圆的参数同上。绘制的填充示意图如下：
在这里插入图片描述

3.3 其他博客

  1. MATLAB求画出的两个椭圆的相交部分的面积
    https://sa93g4.smartapps.baidu.com/pages/squestion/squestion?qid=1516340021111183740&rid=2892952722&eid=10889&_swebfr=1&_swebFromHost=vivobrowser

该文给我提供了宝贵的改进思路！

该文利用蒙特卡罗方法计算两椭圆重合面积实现的图如下：
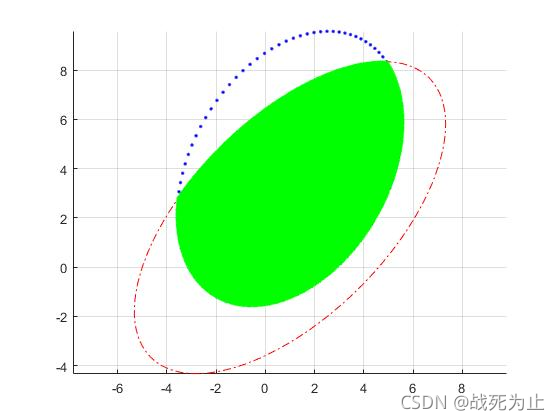
在这里插入图片描述

  1. MATLAB蒙特卡洛（Monte Carlo）方法求椭圆面积
    https://blog.youkuaiyun.com/namishizi321/article/details/105945904

该文利用蒙特卡罗方法计算直线和椭圆的交叉面积计算，实现的图如下：
在这里插入图片描述

4. 蒙特卡罗两椭圆重合面积的计算及填充

本文虽然只实现了同心椭圆的重合面积的代码，但不同心的情况只需给函数增加俩参数，修改撒豆子的面积和重叠面积约束即可。

此处只给出一张效果图如下：
在这里插入图片描述

结语

第50篇，这也是近期我最满意的一篇了

从第1篇到现在，已经过了2年8个月。
专业不对口的日子不好过，路漫漫。
祝妈妈生日快乐~

个人水平有限，有问题欢迎各位大神批评指正！

基于matlab实现的水果识别系统设计
热情、奔放、快乐编程！
01-13 4502
本项目针对多种常见水果混合的图像，利用 Matlab 软件，对水果的识别进行研究。根据水果和背景的差别选取阈值，对去噪增强对比度后的图像进行二值化处理。再对图像进行边缘检测，选定连通区域，标记后再对不同种水果的颜色，形状，大小等特征进行快速识别水果，从而实现对水果的正确分拣。：水果识别、MATLAB、数字图像处理。
MATLAB算法实战应用案例精讲-【图像处理】缺陷检测（补充篇）（附matlab实现代码）
qq_36130719的博客
12-15 5825
差异模型（Variation Model）使用标准图像与待检测图像灰度值相比较，来判断产品是否OK，适用于印刷品检测及产品表面检测。
求两个椭圆相交的面积问题
09-16
描述 最近天文学家发现了一对奇特的卫星，分别命名为A和B。我们知道，卫星通常以椭圆轨道移动，A和B也一样。但是他们的轨迹非常特殊： （1）他们的轨迹在同一平面，具有相同的圆心。 （2）连接两个焦点组成的部分互相垂直。 如果我们将中心标为O，A的焦点为F1和F2，我们就可以建立笛卡尔坐标，O点为圆心，通过F1和F2的为X轴。 下面是一个例子： 天文学家想了解卫星更多东西，他们决定计算其相交面积。不幸的是，计算相交的面积有点难，且他们不会计算，他们求助于天才程序员的你帮忙。现在你的任务是：给定两个满足上述要求的椭圆，计算相交面积。 输入 输入包括多个测试用例。第一行为测试用例个数n（n<=100）。 在每一个测试用例包含两行，第一行A的描述轨迹，另一行描述B的轨迹，每一个描述包含两个整数a，b（a，b<=100）表示椭圆方程X2/a2+Y2/b2=1，并保证A的焦点在X轴上，B的焦点在Y轴上。 输出 对每个测试用例，用一行输出相交面积，用实型数表示，要求精确到小数点后三位。 样例输入 12 11 2 样例输出 3.709
MATLAB 求两张大小完全相同二值图像图像的白色区域重叠面积
rainUstop的博客
05-24 7110
如下图，两副大小完全相同的二值图像，现求取白色区域的重叠面积左侧图像为test01.jpg，右侧为test02.jpg。思路为1.使用imsubtract将两副图像进行相减操作，假设为test01-test02,则imsubtract（test01，test02）,相减之后如下图2.areaTest01-上图白色区域的面积，即为二者重叠区域的面积。1°：读取两副图像，并将其转换为二值图像funct...
matlab之俩矩形框的重叠面积及重叠率
Shmilysi的博客
11-24 8868
function ratio = DecideOberlap(Reframe,GTframe) %Reframe(x,y,w,h) x,y为左上角坐标     x1 = Reframe(1);     y1 = Reframe(2);     width1 = Reframe(3);     height1 = Reframe(4);     x2 = GTframe(1);
matlab计算圆重叠面积,matlab求n个相交圆的面积
weixin_42488542的博客
03-17 4104
目标：在限定区域求n=20个圆的覆盖面积圆心随机抛洒，存在两方面的问题：1)圆心所在的覆盖圆盘处于边界区域，覆盖范围越界2)圆与圆之间相交，存在覆盖面积的重复必须减去这2部分的越界和重复面积。问题：相交圆面积求解时，分别以第一个圆心与其他点判断欧氏距离d，d<2R时候相交 可以几何知识求解。当考虑3圆4圆n个圆相交，如何求其覆盖面积程序如下：clearR=10;A=rand(20,2)*10...
MATLAB 计算相交面积
03-25
计算深度学习中的参数，召回率、准确率和F1-measure这三个参数，通过matlab计算出相交面积计算出结果
两个圆重合部分面积matlab
07-28
- *1* *2* *3* [MATLAB 两椭圆重合面积的填充与计算](https://blog.youkuaiyun.com/qq_34122861/article/details/121429870)[target="_blank" data-report-click={"spm":"1018.2226.3001.9630","extra":{"utm_source":"vip...
基于形态学滤波去噪matlab代码
04-29
- **腐蚀**：通过一个结构元素（通常是矩形、圆或椭圆）在图像上滑动，将与结构元素不完全重合的像素删除，可消除小的噪声点。 - **膨胀**：与腐蚀相反，膨胀是将结构元素覆盖的所有像素添加到图像中，可填充图像...
Matlab专题四
weixin_41949409的博客
09-13 1717
一、二维曲线 1、plot函数 （1）plot函数绘制二维折线（ plot(x,y)包含两个向量 x，y ） >> x = [2.5,3.5,4,5]; >> y = [1.5,2.0,1,1.5]; >> plot(x,y) %运行结果如下 （2）最简单的plot函数调用格式（ plot(x) 只包含一个向量x，此时二维图形横坐标为向量x的下标，纵坐标为向量内的值。 ） >> x = [2,1,3,0]; >&...
计算重合图像的面积
10-16
计算两张图像的重合率，如果有一个标准数据集，一个程序计算的数据集，计算两个数据集的准确率、召回率及F1-measure；将两个图像进行点乘，重叠区域面积S，标准数据集面积S1，程序计算得到的数据集面积S2，则召回率=重合面积S/标准数据集面积S1；精确率=重合面积S/程序计算数据集面积S2；F1=2*S/(S1+S2)。
circtriolap.m:计算通常放置的三角形和圆形的重叠面积。-matlab开发
05-30
计算通常放置的三角形和圆形的平面重叠区域。 圆以 0,0 为中心，半径为 R。三角形由 (3) 个二维顶点向量（或由 3 x 2 矩阵）指定。 第一个参数是 R，第二到第四个参数是顶点。 Th 输出是公共区域 (A)，以及圆外的顶点数 (vout)。
蒙特卡洛法求椭圆面积的MATLAB
04-24
蒙特卡洛法求椭圆面积的MATLAB 部分源码 clear n=500000; % 随机生成n个点 x=rand(1,n); y=rand(1,n);
matlab实现计亩，多边形面积计算，相交面积计算
最新发布
09-20
之前一个农业计亩系统开发的时候，测试的一个计亩算法案例 主要是计算每一行的总面积，以及重叠面积
matlab计算两个图像重叠面积,如何用matlab画出两组实验测定数据概率密度曲线，求两条曲线重叠部分面积 - 数学 - 小木虫 - 学术 科研 互动社区...
weixin_42311375的博客
03-16 1227
matlab>> syms x;>> y1=normpdf(x,2.42,0.16);>> y2=normpdf(x,5.44,0.8);>> x0=solve(y1-y2,'x')x0 =2753/1200 - (2*(75*log(18062160261735236) - 75*log(3612432052347047) + 570025/102...
matlab求两幅图像指定多边形的相交面积
zhrh0096的专栏
04-10 4758
BWa = roipoly(imgs,Xa,Ya); BWb = roipoly(imgs,Xb,Yb); overlap = and(BWa,BWb); 而且为什么要做差值呢？我没看错的话你应该是要求图片中相交的区域吧。 f=imread('luntan1.jpg'); f=rgb2gray(f); f=im2bw(f,0.005); g=imread('lun
matlab计算椭圆的面积,椭圆围绕MATLAB中的数据
weixin_33362096的博客
03-16 1090
考虑代码：%# generate datanum = 50;X = [ mvnrnd([0.5 1.5], [0.025 0.03 ; 0.03 0.16], num) ; ...mvnrnd([1 1], [0.09 -0.01 ; -0.01 0.08], num) ];G = [1*ones(num,1) ; 2*ones(num,1)];gscatter(X(:,1), X(:,2),...
指定区域内实现多尺度、多维度2D图形随机填充(如圆、椭圆、多边形)之MATLAB实现
configBlog
12-10 2644
功能展望：在完美实现二维(2D)空间的所有相关功能后，randFill还将进军三维(3D)空间，实现诸如球体、椭球体、锥体、柱体与多面体等3D图形的随机填充，最终实现2D与3D建模与有限元计算模型联合起来，实现真正的应用。拿到源代码的伙伴应该会发现randCircle函数其实或多或少是有些问题的，比如，在处理穿过边界的圆时并不真实对越界部分进行切除而且通过坐标轴限制来移到相应的视区效果。很显然这与实际的颗粒堆叠或者说分布是不太相符的，更为致命的是仅支持圆的随机填充，对其他更加复杂的几何图形却无能为力。
matlab计算多重复杂多边形重叠面积
configBlog
07-11 2961
最近在学习中遇到了求多边形图像重叠面积问题，经查阅资料发现polyshape函数可以解决此问题，下面总结一下本次学习的心得：Polyshape函数的调用形式为：pgon =polyshape(x,y) 从由 x 坐标向量和对应的 y 坐标向量定义的二维顶点创建 polyshape。x 和 y 的长度必须相同，且至少要有三个元素。这里我们以四个不规则五边形来举例，首先导入多边形：poly1 = po...
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值