leetcode习题集——22. 括号生成（括号表达式）

题目

给出 n 代表生成括号的对数，请你写出一个函数，使其能够生成所有可能的并且有效的括号组合。

例如，给出 n = 3，生成结果为：

[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]

算法1

public class P22_GenerateParentheses2 {
    public List<String> generateParenthesis(int n) {
        List<String> fl = new ArrayList<String>();
        Map<String,String> smap = new HashMap<>();

        if(n==1) {
            fl.add("()");
        }else if(n>1){
            for(int i=1;i<n;i++){
                List<String> l = generateParenthesis(i);
                List<String> r = generateParenthesis(n-i);
                for(String sl : l){
                    for (String sr : r){
                        if(sl.equals("()")){
                            smap.put("("+sr+")","1");
                        }
                        smap.put(sl+sr,"1");
                    }
                }

            }
        }
        if(!smap.isEmpty()){
            for(String key :smap.keySet()){
                fl.add(key);
            }
        }
        return fl;
    }
}

思路：使用递归的方式暴力求解，用Hashmap来去重。

算法2

public class P22_GenerateParentheses3 {
    public List<String> generateParenthesis(int n) {
        List<String> res = new ArrayList<String>();
        generate(res, "", 0, 0, n);

        return res;
    }
    //count1统计“(”的个数，count2统计“)”的个数
    public void generate(List<String> res , String ans, int count1, int count2, int n){

        if(count1 > n || count2 > n) return;

        if(count1 == n && count2 == n)  res.add(ans);


        if(count1 >= count2){
            String ans1 = new String(ans);
            generate(res, ans+"(", count1+1, count2, n);
            generate(res, ans1+")", count1, count2+1, n);

        }
    }

}

思路：深度优先遍历，下图展示了遍历过程（n=2）

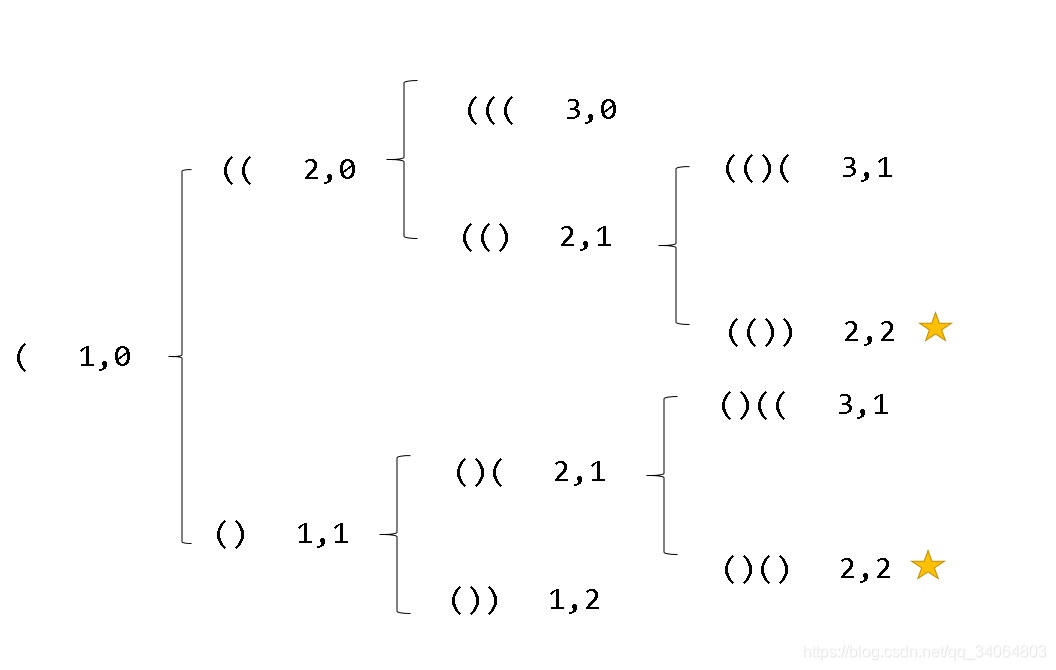
退出遍历条件：count1或count2大于n，count1 >= count2保证了括号表达式的正确性