移动服务(dp）

移动服务

状态设置：f[i][x][y]表示已经处理完前i个请求，且三个服务员分别在p[i], x, y的所有方案的集合；
f[i][x][y]的值是集合中所有方案的花费的最小值；

状态转移：
有两种状态转移方式


一种是一个状态由上一层的三种情况得到，一种是一个状态向下一种状态转移时只有三种情况，显然后者对于此题较为好算，也就是用i计算i+1的值。

因为向下一个状态枚举时，一定有一个状态位于p[i]处，另外两个位于x和y处，就此可以有三种状态向下一个状态枚举，而对于最开始时,也就是p[0]处，状态可以任意设置如：

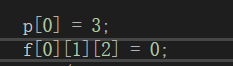
可理解为在0时，p[0]所处的位置为3，其他两个位置分别为1和2，同理

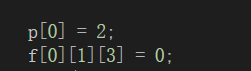
也是一样的。

状态转移代码：

p[0] = 2;
	f[0][1][3] = 0;
	for (int i = 0; i <n; i++)
	{
		for(int x=1;x<=l;x++)
			for (int  y= 1; y <= l; y++)
			{
				int z = p[i];
				if (z == x || z == y || x == y)continue;

				f[i + 1][x][y] = min(f[i+1][x][y],f[i][x][y] + w[p[i]][p[i + 1]]);
				f[i + 1][p[i]][y] = min(f[i + 1][p[i]][y], f[i][x][y] + w[x][p[i + 1]]);
				f[i + 1][x][p[i]] = min(f[i + 1][x][p[i]], f[i][x][y] + w[y][p[i + 1]]);
			}
	}

最终答案从f[m][1…n][1…n]取最小值即可。