博弈论之Nim游戏

•Nim游戏的形式：n堆石子（第i堆有a_i个石子），两人轮流取。每人每次选其中一堆取走任意多个石子（最少一个），无可取者失败。

•结果：当且仅当

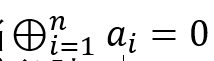
时，先手必败（⊕为异或和，下同）。其它情况下先手必胜。

•策略：游戏的结束状态（石子全部取完）时总体异或和为零，先手失败。未结束时，若总异或和不为零，先手每次选取石子最多的一堆，取剩至数量等于其余石堆的异或和，将总异或和置为零即可；若总异或和为零，无论先手方如何选取，所取的堆石子数必然会从等量于其余石堆的异或和减少，使总异或和不为零。

Nim游戏其实就是取石头，然后今天做了一道这样的题目，是nim游戏的变种。

题目来源 hdu1730 North cott Game

Tom和Jerry正在玩一种Northcott游戏，可是Tom老是输，因此他怀疑这个游戏是不是有某种必胜策略，郁闷的Tom现在向你求救了，你能帮帮他么？
游戏规则是这样的：
　　如图所示，游戏在一个n行m列（1 ≤ n ≤ 1000且2 ≤ m ≤ 100）的棋盘上进行，每行有一个黑子（黑方）和一个白子（白方）。执黑的一方先行，每次玩家可以移动己方的任何一枚棋子到同一行的任何一个空格上，当然这过程中不许越过该行的敌方棋子。双方轮流移动，直到某一方无法行动为止，移动最后一步的玩家获胜。Tom总是先下（黑方）。

图1是某个初始局面，图二是Tom移动一个棋子后的局面（第一行的黑子左移两步）。