算法与数据结构之二叉搜索树

搜索树与二叉搜索树

搜索树是一种可以进行插入、搜索、删除等操作的数据结构。它可以用作字典或者优先级队列。

二叉搜索树是最基本的搜索树。它的各个结点都有键值，并且满足以下的条件：

设x是二叉搜索树中的结点，y是它的左子树中的结点，那么，y的键值≤x的键值。

根据这一特点，我们就能实现一棵二叉搜索树。

二叉搜索树的插入

根据上述的二叉搜索树的特征，我们就能很方便的实现将元素插入到二叉搜索树中。

如果待插入结点的键值小于当前结点的键值，那么就在左子树中递归地执行上述操作，直至待插入结点被插入到二叉树的一个叶结点后面，成为新的叶结点。

这个插入算法的时间复杂度为O(h)，其中h是二叉树的高。

二叉搜索树的搜索

二叉搜索树的搜索过程和插入过程相似，就是不断比较关键字和当前结点的键值之间的关系，然后在相应的子树中查找。如果当前结点的键值等于关键字，那么就是找到了。如果直到搜索到叶结点也无法匹配到关键字，那么就说明这个关键字不存在于这棵二叉搜索树之中。

二叉搜索树的删除

这是一个有难度的问题。

二叉搜索树的删除需要在删除结点后，仍然满足二叉搜索树的结构。那怎么办呢？我们要删除某个结点，那么我们只需要把这个结点的左子树中键值最大的结点的值复制到当前结点，然后删除被复制的那个结点。或者删除右子树中键值最小的结点，并把键值复制到当前结点。

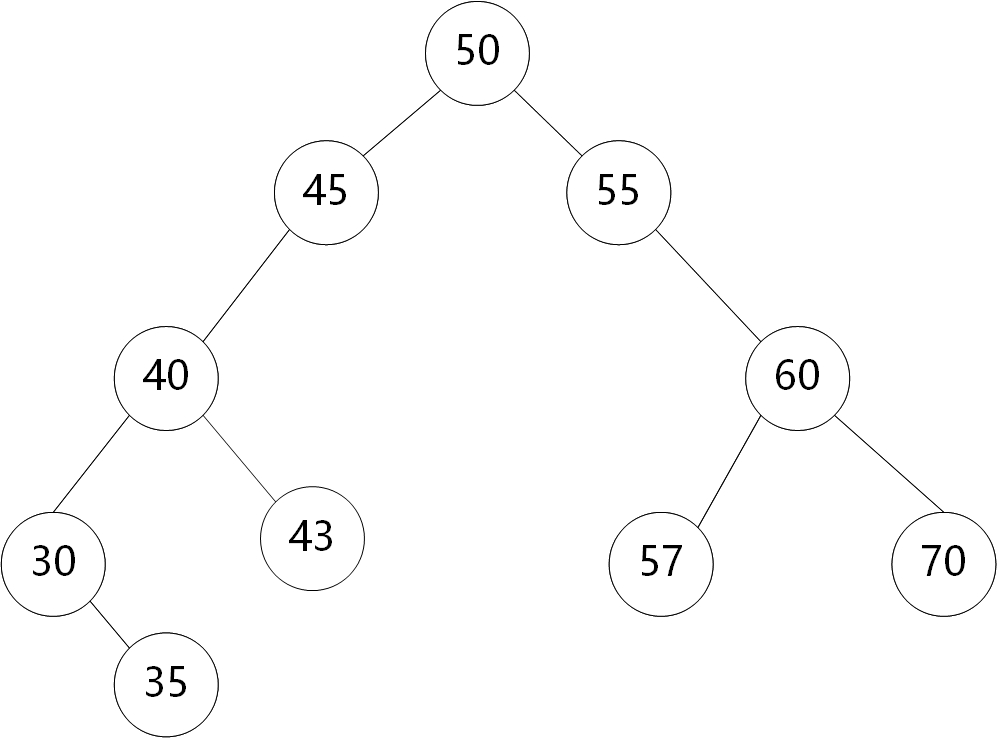
感觉有点绕，那么就把上面这棵二叉搜索树当个例子来讲。

情况1：

我们要删除键值为35的结点，那么只需要把30号结点的右子结点指向空结点，然后把键值为35的结点free掉就可以了。

情况2：

我们要删除键值为55的结点，那么我们在55的右子树中寻找键值最大的结点，也就是70结点。接着把55结点的键值赋值为70，最后把最下端的70结点free掉就可以了。然后会发现，删除后仍然满足二叉搜索树的结构。

情况3：

对于下面这棵二叉搜索树：

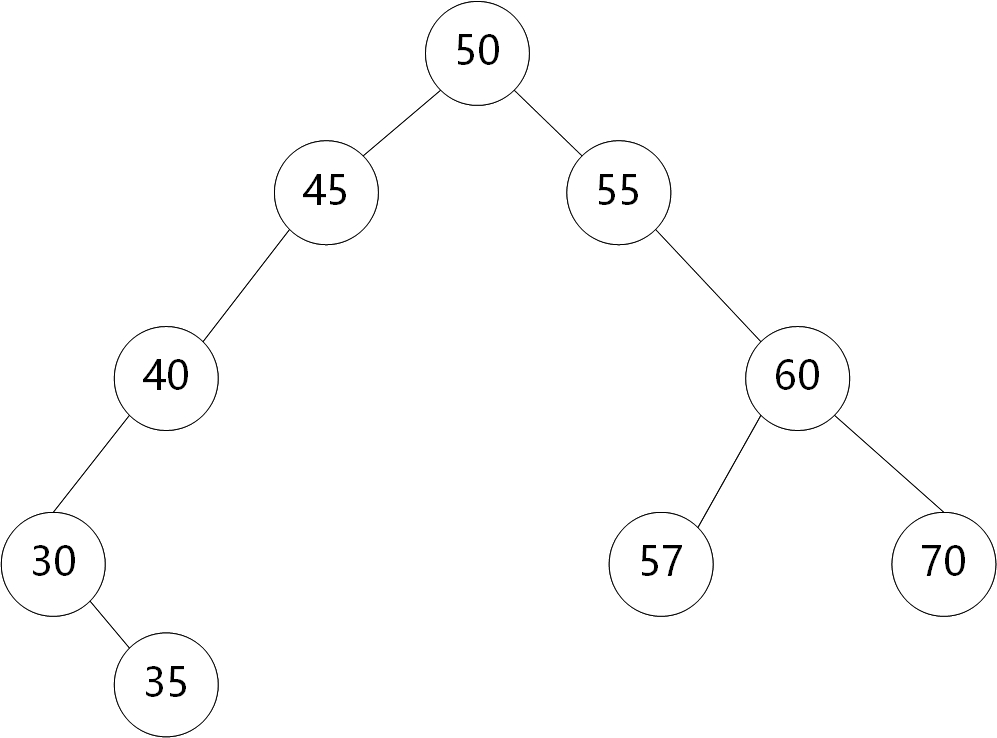
我们要删除40号结点，这个结点没有右子树。那怎么办呢？分析可以知道，我们只需要把45结点和30结点连接起来。然后把40结点free掉。我在这里就要实名点名一下《挑战程序设计竞赛2》中的方法。书上讲的是向上查找第一个非空的且当前结点不是父节点的右子结点的结点。那个方法真是把人都给绕晕了。其实分析就可以发现，在当前结点的右子树不存在的时候，只需要把当前结点的左子树接到当前结点的父节点的左边，然后把当前节点free掉就好了。这就很简单地解决了，并且代码量比书上的少了不少。

有图有真相，下面是书上的程序的评测结果

然后我的方法：

代码量减少了，运行时间差不多。而且真的好理解很多！

代码实现

题目位于

http://judge.u-aizu.ac.jp/onlinejudge/description.jsp?id=ALDS1_8_C

#include<iostream>
#include<cstdlib>
#include<string>
#include<cstdio>
using namespace std;

struct Node
{
    int key;
    Node *parent,*left,*right;
};

Node *root;
Node *NIL;

//插入元素到二叉树里面
void ins(int k)
{
    Node *this_node = root;
    Node *last_node = NIL;
    Node *insert_node;
    //设置待插入的节点的属性
    insert_node = (Node*)malloc(sizeof(Node));
    insert_node->key = k;
    insert_node->left = NIL;
    insert_node->right = NIL;

    while(this_node!=NIL)
    {
        last_node = this_node;
        if(insert_node->key<this_node->key)
        {
            this_node = this_node->left;
        }
        else this_node = this_node->right;
    }
    insert_node->parent = last_node;//把节点接在正确的位置
    if(last_node==NIL)
        root = insert_node;
    else
    {
        if(insert_node->key<last_node->key)
        {
            last_node->left = insert_node;
        }
        else last_node->right = insert_node;
    }



}


Node* search_tree(int k)
{
    Node *this_node = root;
    while(this_node!=NIL && k!=this_node->key)
    {
        if(k<this_node->key)
            this_node = this_node->left;
        else
            this_node = this_node->right;
    }

    return this_node;
}


void inorder(Node *this_node)
{
    if(this_node==NIL) return;
    inorder(this_node->left);
    printf(" %d", this_node->key);
    inorder(this_node->right);
}


void preorder(Node *this_node)
{
    if(this_node==NIL) return;

    printf(" %d", this_node->key);
    preorder(this_node->left);
    preorder(this_node->right);

}

Node * get_minimum(Node * this_node)
{
    while(this_node->left!=NIL)
        this_node = this_node->left;
    return this_node;
}

void delete_node(int k)
{
    Node * this_node = search_tree(k);
    Node *to_delete;
    Node *to_delete_son;
    if(this_node->left==NIL||this_node->right==NIL)
    {
        to_delete = this_node;
    }
    else
    {
            to_delete = get_minimum(this_node->right);
            this_node->key = to_delete->key;
    }

    if(to_delete->left!=NIL)
        to_delete_son = to_delete->left;
    else to_delete_son = to_delete->right;


    if(to_delete_son!=NIL)
    {
        to_delete_son->parent = to_delete->parent;
    }


    if(to_delete->parent==NIL)
        root = to_delete_son;
    else
    {
        if(to_delete->parent->left==to_delete)
        {
            to_delete->parent->left = to_delete_son;
        }
        else
        {
            to_delete->parent->right = to_delete_son;
        }

    }

    free(to_delete);



}




int main()
{
    int m;
    cin>>m;
    string cmd=" ";
    int num;
    for(int i=0;i<m;i++)
    {
        cin>>cmd;
        if(cmd=="insert")
        {
            cin>>num;
            ins(num);
        }
        else if(cmd=="find")
        {
            cin>>num;
            Node *res = search_tree(num);
            if(res==NIL)
                cout<<"no"<<endl;
            else cout<<"yes"<<endl;
        }
        else if(cmd=="delete")
        {
            cin>>num;
            delete_node(num);
        }
        else
        {

            inorder(root);
            cout<<endl;
            preorder(root);
            cout<<endl;
        }
    }

}

欢迎关注我的公众号哦！