[论文解读] DeepCT:Tomographic Combinatorial Testing for Deep Learning Systems

DeepCT: Tomographic Combinatorial Testing for Deep Learning Systems

简介

论文标题

• DeepCT: Tomographic Combinatorial Testing for Deep Learning Systems
• DeepCT：深度学习系统的层析组合测试
• 2019

贡献

• 提出了一套专门针对DL系统的组合测试准则
• 我们还提出了一种通用的CT覆盖引导的DL系统测试生成技术。·
• 我们对DeepCT进行了研究，以证明CT在DL测试中的潜在用处。

论文提出了几个层覆盖标准,并给出了一基于该标准的测试生成算法,并证明该算法比随机选择用例生成更能找到对抗用例

摘要

深度学习(DL)在过去的十年中取得了显著的进步，并在许多工业领域得到了广泛的应用。然而，DL系统的鲁棒性近年来受到极大的关注，输入的微小扰动可能会导致DL故障。当DL系统部署到安全关键型应用程序时，这些健壮性问题可能会潜在地导致严重后果，并阻碍DL系统的实际部署。测试技术能够在早期阶段对DL系统进行健壮性评估和易受攻击问题的检测。测试DL系统的主要挑战在于其输入的高维性和巨大的内部潜在特征空间，这使得测试每个状态几乎是不可能的。对于传统软件来说，组合测试(CT)是一种平衡测试探索和缺陷检测能力的有效测试技术。在本文中，我们对下行系统中的CT进行了探索性的研究。我们提出了一套专门针对DL系统的组合测试准则，以及一种CT覆盖制导的测试生成技术。我们的评估表明，CT为测试DL系统提供了一条很有前途的途径。

层析组合的背景和动机

传统CT

CT : Combinatorial testing 组合测试

了在获得期望的CT覆盖率的同时最小化测试集大小，CT通常将测试生成问题转化为约束求解问题。因此，对CT[10]的研究经历了一次向约束CT的转变，它被分解为元启发式方法[11]、基于SAT的方法[12]和贪婪方法[13]。

DL CT

为了更好地推动这项工作，我们从以下两个角度讨论了本文的意图：

PER1：为什么是“层析 ‘tomographic’,”，即CT侧重于每层内更密集的测试？

PER2：为什么是“组合 ‘combinatorial’,”，即CT系统地检查每层内神经元之间的相互作用？

PER1:

对于CNN，一个主要的假设是数据(图像、视频、音频)是由模式组成的：本地的、固定的，最重要的是，多尺度(分层)。因此，为了测试DNN模型的稳健性，由于DNN函数在不同的尺度上具有不同的层次，因此对它进行逐层测试并像计算机层析扫描一样系统地探索其潜在特征空间是一种很好的做法。因此，我们称之为“tomographic”。

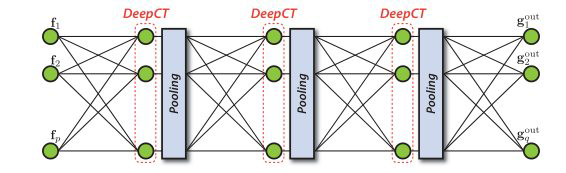
图1：对于CNN，特征由多个卷积和汇聚层组成。DeepCT检查每一层内神经元之间的相互作用，就像计算机断层扫描一样。

PER2：

至于PER2，有几个有趣的方面需要讨论。首先，如果我们放大到DNN中的两个相邻层，所有神经元只与下一层的神经元交互(在前向通道中)，而在反向传播期间，所有神经元只与上一层的神经元交互(在后向通道中)。我们可以将这种局部两层结构视为无向二分图形模型，其中该层内不会发生任何交互。这类似于在受限玻尔兹曼机器中所指的‘受限’,图2显示了使用标准卷积、两个变体(本地连接的卷积和平铺卷积)以及本质上是DNN情况的完全连接的版本的两个相邻层之间的相互作用。很明显，每一层内都没有神经相互作用。

逻辑单元之间可能存在逻辑(无形)的相互作用，其中当前层的神经元共同决定其下一层神经元的逻辑。我们想用CT捕捉和检查每一层神经元之间的这些无形的相互作用。因此，我们称之为“combinatorial.”。

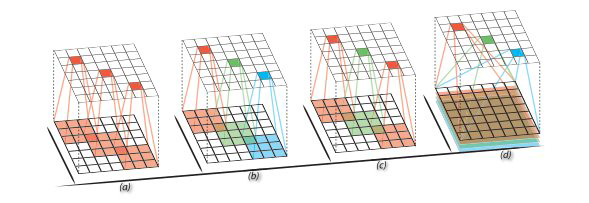
图2：相邻两层之间的相互作用，用于(A)标准卷积，(B)局部连接卷积，©平铺卷积，以及最后(D)全连通情况(DNN)。

组合测试标准

Neuron-activation configuration

我们用$A(ni，x)\in 0，1$来表示神经元$n_i$在给定x的激活状态，其中1对应于激活，而0对应于未激活

对于一组神经元 M = { n 1 , n 2 , … , n k } ⊆ L i M=\left\{n_{1}, n_{2}, \ldots, n_{k}\right\} \subseteq L_{i} M={ n1​,n2​,…,nk​}⊆Li​在第$i$层$l_i$中，M的神经元激活配置是元组 c = ( b 1 , b 2 , … , b k ) c=\left(b_{1}, b_{2}, \dots, b_{k}\right) c=(b1​,b