极大似然估计(Maximum Likelihood Estimation,简称 MLE),也被翻译成最大似然估计,是一种通过样本量获得模型最优参数的方法。
例如极大似然估计可以估计概率密度函数的参数,比如一批样本/数据集/统计量(可能)符合正态分布,那么我们只要找到这个数据集的均值和方差或者标准差,就可以得到符合该数据集的概率密度公式。
f(x)=12πσ2e−(x−μ)22σ2
f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x - \mu)^2}{2\sigma^2}}
f(x)=2πσ21e−2σ2(x−μ)2
其中:
- μ\muμ 表示均值
- σ2\sigma^2σ2 表示方差
- xxx 是随机变量的取值
极大似然估计的流程
极大似然估计的流程为:
- 确定概率模型:例如是符合正态分布模型。
- 构建似然函数:也就是把所有概率密度函数相乘。
或者我们可以将其变成对数函数,这样连乘就变成连加了,在一些情况下这样更方便。而且对于计算机来说,加的成本要比乘要低。
这里额外说一句,虽然函数是连续的,但是由于样本是离散的,这个概率密度函数是“离散”的,所以可以连乘。这部分你看代码就知道了。
- 求解对数似然函数的最大值
每一点就是我们把当前这点的 xxx 带入(比如标准正态分布函数),而似然函数的自变量是参数。然后我们对其求导就可以找到这个极大似然估计参数的最优解。
对于程序实现来说,求导我们可以知道需要变化的方向。
通过极大似然估计演示机器如何学习参数
虽然你可能是因为考试搜到这篇文章,但是极大似然估计基本上你在知道原理后就是背公式了。所以我们还是继续通过代码来演示是如何得到估计参数的。
我们现在随便找一组正态分布密度函数的参数,例如 μ=7.2\mu = 7.2μ=7.2,σ=2.8\sigma = 2.8σ=2.8,也就是 σ2=7.83999\sigma^2 = 7.83999σ2=7.83999。
我们现在想从标准正态分布开始(你也可以从其他的开始),不断调整参数,最后符合我们要的这个参数(下面将其称为目标参数)。
这里我们通过目标参数先生成 10000 个数据当做样本,然后通过这个样本去拟合参数。
这里和解题方法不同的地方在于:第一,我们这次要找到两个参数值,而不是一般考试中的求一个估计参数,第二,我们不是通过求导找到这个值。
下面是一些关键代码(解释看注释),完整的看后面:
def __init__(self):
# 目标分布参数
self.target_mu = 7.2 # 理论均值
self.target_sigma = 2.8 # 理论标准差
self.target_var = self.target_sigma **2 # 理论方差
# MLE估计参数
self.mle_mu = 0.0 # 均值估计
self.mle_sigma = 1.0 # 标准差估计
self.mle_var = self.mle_sigma** 2 # 方差估计
然后生成数据:
def generate_data(self, n_samples=100000):
"""生成观测数据"""
self.data = np.random.normal(
loc=self.target_mu,
scale=self.target_sigma,
size=n_samples
)
print(f"Generated {n_samples} data points from N(μ={self.target_mu}, σ²={self.target_var:.2f})")
# 理论MLE值(样本统计量)
# 需要注意样本统计量还是和理论值略有不通,后面你可以看到
self.true_mle_mu = np.mean(self.data)
self.true_mle_var = np.var(self.data, ddof=0)
self.true_mle_sigma = np.sqrt(self.true_mle_var)
return self.data
然后就可以进行极大似然估计了:
def mle_gradient_descent(self, epochs=10000, lr=0.05, tol=1e-8):
# 由于这里没有单独测试集,所以手动划分一下训练集和测试集
# 这个技巧属于最常见的方法了
train_data, val_data = train_test_split(self.data, test_size=0.2, random_state=42)
# 这里设置当前参数为初始值
self.mle_mu = self.initial_mu
self.mle_var = self.initial_var
self.mle_sigma = np.sqrt(self.mle_var)
# 这下面的都是为了输出训练情况和生成图
self.train_log_likelihoods = []
self.val_log_likelihoods = []
self.epochs_record = []
best_val_ll = -np.inf
best_mu, best_var = self.mle_mu, self.mle_var
# 这个是给防止过拟合的早停机制用的
counter = 0
# 开始训练
for epoch in range(epochs):
# 转换成对数好计算
# loc=self.mle_mu 位置参数(均值)
# scale=np.sqrt(self.mle_var)(标准差)
# 转换成对数后,那么就是对数化概率密度的总和,加法成本更低。
# 需要注意这个值越接近 0,说明模型对训练数据的拟合效果越好。
train_ll = np.sum(stats.norm.logpdf(train_data, loc=self.mle_mu, scale=np.sqrt(self.mle_var)))
val_ll = np.sum(stats.norm.logpdf(val_data, loc=self.mle_mu, scale=np.sqrt(self.mle_var)))
# 这部分代码是生成图的
self.train_log_likelihoods.append(train_ll)
self.val_log_likelihoods.append(val_ll)
self.epochs_record.append(epoch + 1)
# 训练集与学到的均值的差异
error = train_data - self.mle_mu
# 计算均值的梯度
grad_mu = np.mean(error / self.mle_var)
# 训练集与学到的方差的差异
mean_squared_error = np.mean(error **2)
# 计算方差的梯度
grad_var = (-1/(2*self.mle_var)) + (mean_squared_error)/(2*self.mle_var** 2)
# 开始学习,每一次加(学习率*梯度)
self.mle_mu += lr * grad_mu
self.mle_var += lr * grad_var
# 因为方差是非负的,所以负值就当 0 了
self.mle_var = max(self.mle_var, 0)
# 计算标准差,这里是给早停机制用的
# 因为我们最开始设计的就是标准差,而不是方差
self.mle_sigma = np.sqrt(self.mle_var)
# 早停机制(如果误差下降后又上升了超过50次,就停止)
if val_ll > best_val_ll:
best_val_ll = val_ll
best_mu, best_var = self.mle_mu, self.mle_var
counter = 0
else:
counter += 1
if counter >= 50 or (abs(val_ll - best_val_ll) < tol):
print(f"\nConverged at epoch {epoch+1}")
self.mle_mu, self.mle_var = best_mu, best_var
self.mle_sigma = np.sqrt(self.mle_var)
break
# 每100个epoch输出一次训练信息
if (epoch + 1) % 100 == 0:
print(f"Epoch {epoch+1}/{epochs} - "
f"Train LL: {train_ll:.2f}, Val LL: {val_ll:.2f}, "
f"MLE Mean: {self.mle_mu:.4f}, MLE Variance: {self.mle_var:.4f}")
return self.train_log_likelihoods
这里解释上面代码中的这部分:
# 计算均值的梯度
grad_mu = np.mean(error / self.mle_var)
# 训练集与学到的方差的差异
mean_squared_error = np.mean(error **2)
# 计算方差的梯度
grad_var = (-1/(2*self.mle_var)) + (mean_squared_error)/(2*self.mle_var** 2)
所谓的梯度和导数,在计算机中往往就是使用最古朴的定义实现的:变化率。而且由于现实当中并不存在“极限”的情况,所以并不像数学中的很复杂(你看代码也可以看出来)。但是方差的梯度还是要自己算一下导数。
首先,对数化似然函数为:
logL(μ,σ2)=−n2log(2π)−n2log(σ2)−12σ2∑i=1n(xi−μ)2
\log L(\mu, \sigma^2) = -\frac{n}{2}\log(2\pi) - \frac{n}{2}\log(\sigma^2) - \frac{1}{2\sigma^2}\sum_{i=1}^n (x_i - \mu)^2
logL(μ,σ2)=−2nlog(2π)−2nlog(σ2)−2σ21i=1∑n(xi−μ)2
对 σ² 求偏导(注意是 σ²,不是 σ):
∂logL∂σ2=−n2σ2+12σ4∑i=1n(xi−μ)2
\frac{\partial \log L}{\partial \sigma^2} = -\frac{n}{2\sigma^2} + \frac{1}{2\sigma^4}\sum_{i=1}^n (x_i - \mu)^2
∂σ2∂logL=−2σ2n+2σ41i=1∑n(xi−μ)2
提取公因子 n2σ2\frac{n}{2\sigma^2}2σ2n 后可写成:
∂logL∂σ2=n2σ2(∑(xi−μ)2nσ2−1)
\frac{\partial \log L}{\partial \sigma^2} = \frac{n}{2\sigma^2} \left( \frac{\sum (x_i - \mu)^2}{n\sigma^2} - 1 \right)
∂σ2∂logL=2σ2n(nσ2∑(xi−μ)2−1)
这里的 nnn 其实并不会影响我们计算(因为它其实就是个固定系数,所以我们可以直接忽略它,这样还减少一次计算),那么可以进一步简化为代码中使用的形式:
∂logL∂σ2=12σ2(∑(xi−μ)2nσ2−1)
\frac{\partial \log L}{\partial \sigma^2} = \frac{1}{2\sigma^2} \left( \frac{\sum (x_i - \mu)^2}{n\sigma^2} - 1 \right)
∂σ2∂logL=2σ21(nσ2∑(xi−μ)2−1)
这里的 μ\muμ 虽然是数学期望(均值),但是在这里,由于我们是从样本中计算,所以我们使用前面算出来的均值。
这是非常重要的一个概念,就是为什么学习率必须要一致。因为你在后面的训练中可以看到,均值收敛的要比方差快得多(因为这里还有个平方,计算复杂)所以我们并不能分别给两个参数使用不同的学习率。
你可以试试看,会发现最后得到的参数误差巨大。
难道就没有办法了吗?有,现在很多模型的训练都是使用变学习率,也就是通过一些机制(例如当损失率下降变慢后,减小学习率,从而提高精度)或一些函数来使用可变学习率。但这不是本博客应该讨论的,所以就不展开了。
然后就可以开始训练了。
下面是完整代码,你可以复制下来自己试试看:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from scipy import stats
from sklearn.model_selection import train_test_split
import os
import time
np.random.seed(42)
class MLENormalEstimator:
def __init__(self):
self.target_mu = 7.2
self.target_sigma = 2.8
self.target_var = self.target_sigma **2
self.initial_mu = 0.0
self.initial_sigma = 1.0
self.initial_var = self.initial_sigma** 2
self.mle_mu = self.initial_mu
self.mle_sigma = self.initial_sigma
self.mle_var = self.initial_var
def generate_data(self, n_samples=100000):
self.data = np.random.normal(
loc=self.target_mu,
scale=self.target_sigma,
size=n_samples
)
print(f"Generated {n_samples} data points from N(μ={self.target_mu}, σ²={self.target_var:.2f})")
self.true_mle_mu = np.mean(self.data)
self.true_mle_var = np.var(self.data, ddof=0)
self.true_mle_sigma = np.sqrt(self.true_mle_var)
return self.data
def mle_gradient_descent(self, epochs=10000, lr=0.05, tol=1e-8):
train_data, val_data = train_test_split(self.data, test_size=0.2, random_state=42)
self.mle_mu = self.initial_mu
self.mle_var = self.initial_var
self.mle_sigma = np.sqrt(self.mle_var)
self.train_log_likelihoods = []
self.val_log_likelihoods = []
self.epochs_record = []
best_val_ll = -np.inf
best_mu, best_var = self.mle_mu, self.mle_var
counter = 0
start_time = time.time()
for epoch in range(epochs):
train_ll = np.sum(stats.norm.logpdf(train_data, loc=self.mle_mu, scale=np.sqrt(self.mle_var)))
val_ll = np.sum(stats.norm.logpdf(val_data, loc=self.mle_mu, scale=np.sqrt(self.mle_var)))
self.train_log_likelihoods.append(train_ll)
self.val_log_likelihoods.append(val_ll)
self.epochs_record.append(epoch + 1)
error = train_data - self.mle_mu
grad_mu = np.mean(error / self.mle_var)
mean_squared_error = np.mean(error **2)
grad_var = (-1/(2*self.mle_var)) + (mean_squared_error)/(2*self.mle_var** 2)
self.mle_mu += lr * grad_mu
self.mle_var += lr * grad_var
self.mle_var = max(self.mle_var, 0)
self.mle_sigma = np.sqrt(self.mle_var)
if val_ll > best_val_ll:
best_val_ll = val_ll
best_mu, best_var = self.mle_mu, self.mle_var
counter = 0
else:
counter += 1
if counter >= 50 or (abs(val_ll - best_val_ll) < tol):
print(f"\nConverged at epoch {epoch+1}")
self.mle_mu, self.mle_var = best_mu, best_var
self.mle_sigma = np.sqrt(self.mle_var)
break
if (epoch + 1) % 100 == 0:
print(f"Epoch {epoch+1}/{epochs} - "
f"Train LL: {train_ll:.2f}, Val LL: {val_ll:.2f}, "
f"MLE Mean: {self.mle_mu:.4f}, MLE Variance: {self.mle_var:.4f}")
end_time = time.time()
self.train_duration = end_time - start_time
return self.train_log_likelihoods
def evaluate(self):
print("\n" + "="*80)
print(" MAXIMUM LIKELIHOOD ESTIMATION RESULTS")
print("="*80)
print(f"1. 训练耗时 (Training Duration): {self.train_duration:.4f} 秒")
print(f"\n2. Target Distribution:")
print(f" - Mean: {self.target_mu:.6f}")
print(f" - Variance: {self.target_var:.6f}")
print(f"\n3. Theoretical MLE (Sample Statistics):")
print(f" - Mean MLE: {self.true_mle_mu:.6f}")
print(f" - Variance MLE: {self.true_mle_var:.6f}")
print(f"\n4. Estimated MLE:")
print(f" - Estimated Mean: {self.mle_mu:.6f}")
print(f" - Estimated Variance: {self.mle_var:.6f}")
print(f"\n5. Initial Parameters:")
print(f" - Initial Mean: {self.initial_mu:.6f}")
print(f" - Initial Variance: {self.initial_var:.6f}")
print(f"\n6. Estimation Errors:")
print(f" - Mean Error: {abs(self.true_mle_mu - self.mle_mu):.8f}")
print(f" - Variance Error: {abs(self.true_mle_var - self.mle_var):.8f}")
print("="*80 + "\n")
# 对数似然图表
plt.figure(figsize=(6, 4))
plt.plot(self.epochs_record, self.train_log_likelihoods, label='Training Log-Likelihood',
color='blue', linewidth=1.2)
plt.plot(self.epochs_record, self.val_log_likelihoods, label='Validation Log-Likelihood',
color='orange', linewidth=1.2)
plt.title('Log-Likelihood During MLE Optimization', fontsize=10)
plt.xlabel('Epoch', fontsize=8)
plt.ylabel('Log-Likelihood (Higher = Better)', fontsize=8)
plt.grid(True, linestyle='--', alpha=0.5)
plt.legend(fontsize=7)
plt.tight_layout()
plt.savefig('corrected_mle_log_likelihood.png', dpi=150)
plt.close()
# 对比图
plt.figure(figsize=(6, 4))
x_min = min(self.data.min(), self.target_mu - 4*self.target_sigma, self.initial_mu - 4*self.initial_sigma)
x_max = max(self.data.max(), self.target_mu + 4*self.target_sigma, self.initial_mu + 4*self.initial_sigma)
x = np.linspace(x_min, x_max, 1000)
plt.hist(self.data, bins=100, density=True, alpha=0.6, color='blue',
label=f'Observed Data (μ={self.true_mle_mu:.2f})')
plt.plot(x, stats.norm.pdf(x, self.target_mu, self.target_sigma), 'g-', lw=2,
label=f'Target Distribution')
plt.plot(x, stats.norm.pdf(x, self.mle_mu, self.mle_sigma), 'r--', lw=2,
label=f'Estimated MLE Distribution')
plt.plot(x, stats.norm.pdf(x, self.initial_mu, self.initial_sigma), 'purple', ls=':', lw=1.5,
label=f'Initial Distribution')
plt.title('Distribution Comparison', fontsize=10)
plt.xlabel('Value', fontsize=8)
plt.ylabel('Probability Density', fontsize=8)
plt.legend(fontsize=7)
plt.grid(alpha=0.3)
plt.savefig('mle_distribution_comparison.png', dpi=150)
plt.close()
print("Generated plots:")
print("1. corrected_mle_log_likelihood.png - Log-likelihood curve")
print("2. mle_distribution_comparison.png - Distribution comparison (with initial curve)")
if __name__ == "__main__":
estimator = MLENormalEstimator()
estimator.generate_data(n_samples=100000)
print("\nStarting maximum likelihood estimation...")
estimator.mle_gradient_descent(
epochs=10000,
lr=0.1,
tol=1e-8
)
estimator.evaluate()
可以看到输出如下(截取最后部分):
Epoch 9600/10000 - Train LL: -195870.32, Val LL: -49077.16, MLE Mean: 7.2181, MLE Variance: 7.8367
Epoch 9700/10000 - Train LL: -195870.32, Val LL: -49077.16, MLE Mean: 7.2181, MLE Variance: 7.8368
Epoch 9800/10000 - Train LL: -195870.32, Val LL: -49077.16, MLE Mean: 7.2181, MLE Variance: 7.8368
Epoch 9900/10000 - Train LL: -195870.32, Val LL: -49077.16, MLE Mean: 7.2181, MLE Variance: 7.8368
Epoch 10000/10000 - Train LL: -195870.32, Val LL: -49077.16, MLE Mean: 7.2181, MLE Variance: 7.8369
================================================================================
MAXIMUM LIKELIHOOD ESTIMATION RESULTS
================================================================================
1. 训练耗时 (Training Duration): 27.8044 秒
2. Target Distribution:
- Mean: 7.200000
- Variance: 7.840000
3. Theoretical MLE (Sample Statistics):
- Mean MLE: 7.202707
- Variance MLE: 7.854133
4. Estimated MLE:
- Estimated Mean: 7.218075
- Estimated Variance: 7.836873
5. Initial Parameters:
- Initial Mean: 0.000000
- Initial Variance: 1.000000
6. Estimation Errors:
- Mean Error: 0.01536817
- Variance Error: 0.01726031
================================================================================
Generated plots:
1. corrected_mle_log_likelihood.png - Log-likelihood curve
2. mle_distribution_comparison.png - Distribution comparison (with initial curve)
你可以看到4. Estimated MLE:与3. Theoretical MLE (Sample Statistics):和2. Target Distribution:非常接近了,而这就花了 27 秒。
当然呢你改变随机数种子也会影响训练情况。
如果你愿意牺牲一些精度来换取更快的速度,那么可以把epoch换的更低,因为均值(MLE Mean)在 1000 epoch 的时候就稳定了,后面都是在训练方差(MLE Variance)了:
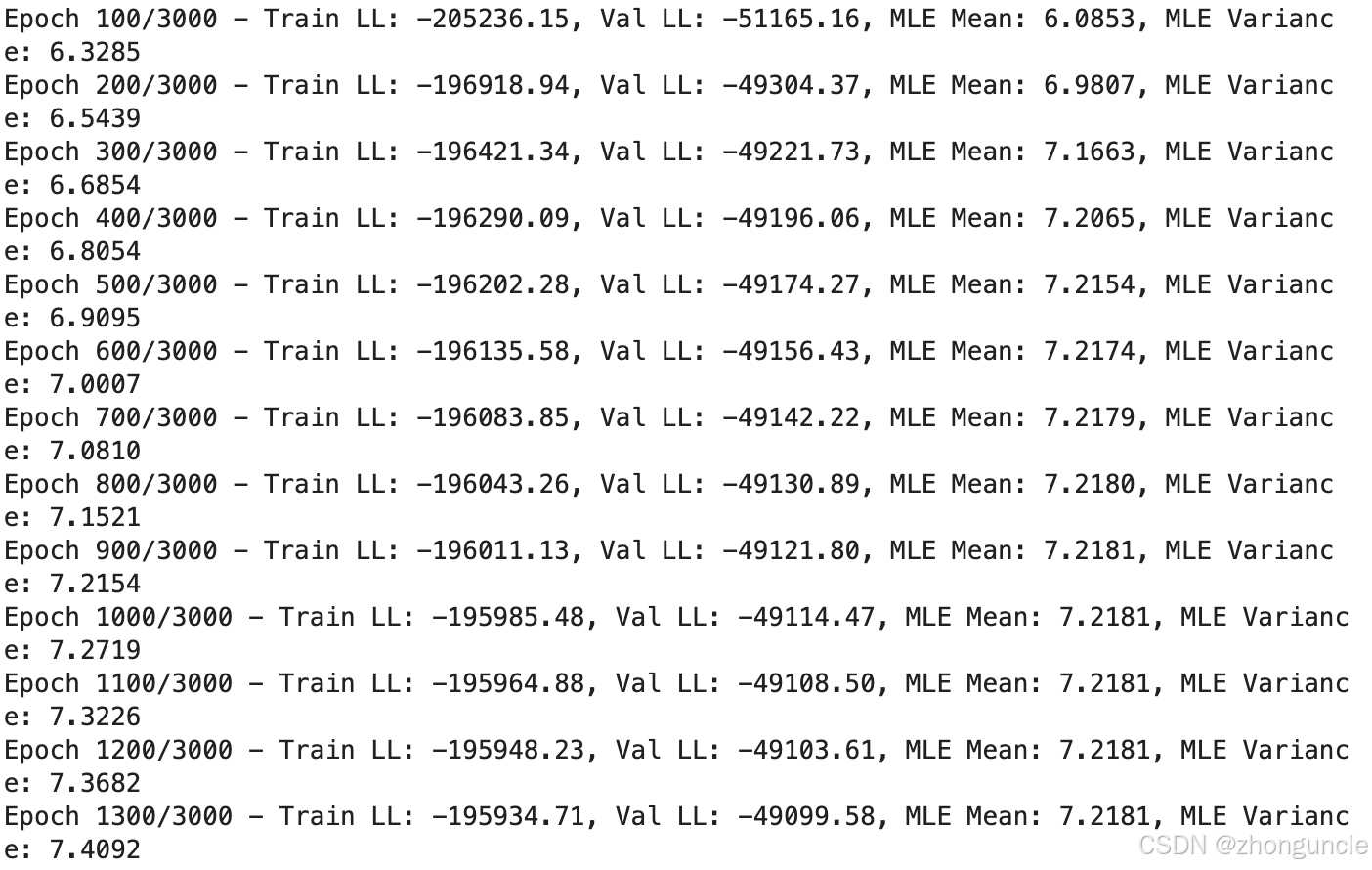
代码中有生成图的部分,这里可以更直观的对比学到的效果:
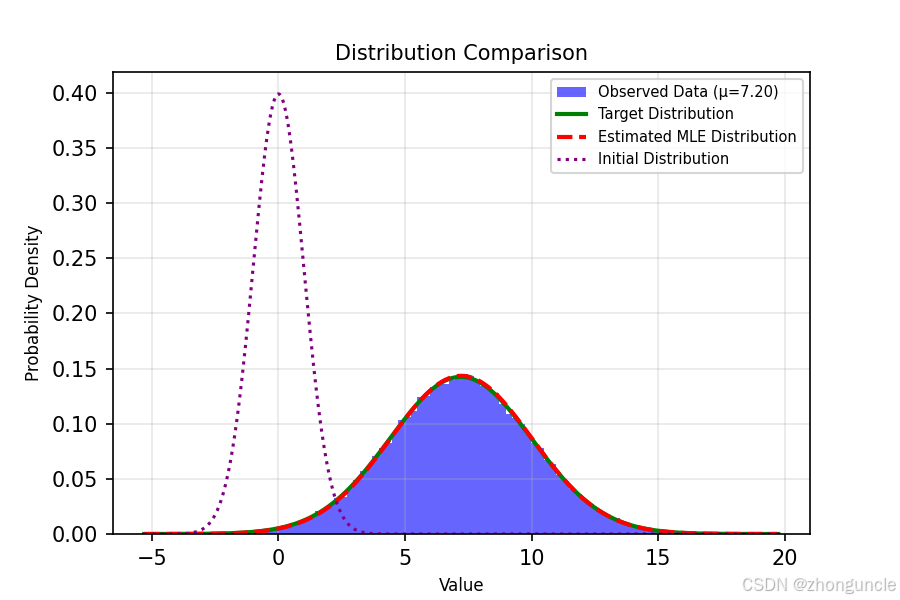
最左边的虚线是标准正态分布的图像(也就是初始情况),蓝紫色是采样的那个数据集(也就是样本/统计量),绿线是目标分布的曲线,红色虚线(这里可能看上去有点像红橙色)是我们拟合参数的曲线,可以看到二者差不多了。
希望能帮到有需要的人~






















 1422
1422

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










