高斯消元的学习

最新推荐文章于 2024-01-07 02:10:14 发布

Eminem1147

最新推荐文章于 2024-01-07 02:10:14 发布

阅读量489

点赞数 1

分类专栏：高斯消元

高斯消元专栏收录该内容

2 篇文章

订阅专栏

以下内容来自转载：

高斯消元

算法目的：
高斯消元，一般用于求解线性方程组AX = B（或模线性方程组AX mod P = B），以四个未知数，四个方程为例，AX=B表示成4x4的矩阵和4x1的矩阵相乘的形式：

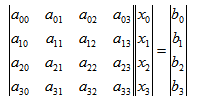
其中A和B(b0 b1 b2 b3)已知，要求列向量X(x0 x1 x2 x3)的值。

算法核心思想：
对于n个方程，m个未知数的方程组，消元的具体步骤如下：

1、枚举第i (0 <= i < n) 行，初始化列为col = 0，每次从[i, n)行中找到第col列中元素绝对值最大的行和第i行进行交换(找到最大的行是为了在消元的时候把浮点数的误差降到最小)；

a) 如果第col列的元素全为0，放弃这一列的处理，col+1，i不变，转1)；

b) 否则，对于所有的行j (i < j < n)，如果a[j][col]不为0，则需要进行消元，以期第i行以下的第col列的所有元素都消为0（这一步就是线性代数中所说的初等行变换，具体的步骤就是将第j行的所有元素减去第i行的所有元素乘上一个系数，这个系数即a[j][col] / a[i][col]）。

2、重复步骤1) 直到n个方程枚举完毕或者列col == m。

3、判断解的情况：

a) 如果出现某一行，系数矩阵全为0，增广矩阵不全为0，则无解（即出现[0 0 0 0 0 b]，其中b不等于0的情况）；

b) 如果是严格上三角，则表明有唯一解；

c) 如果增广矩阵有k (k > 0)行全为0，那么表明有k个变量可以任意取值，这几个变量即自由变量；对于这种情况，一般解的范围是给定的，令解的取值有T个，自由变量有V个，那么解的个数就是 TV。

算法复杂度：
O(n³)

ACM中的高斯消元题型一般涉及到的有：

1、浮点数消元

系数矩阵为整数或浮点数，消元的时候乘上的系数为浮点数，一般用于求解浮点数解，例如HDU 3359；

2、整数消元

系数矩阵全为整数，消元的时候乘上的系数均为整数，整个消元过程不出现浮点数。由于乘法很容易溢出，一般很少用。

3、模线性方程组

系数矩阵全为整数，消元的时候乘上的系数均为整数，每次运算都模上一个数P，整个消元过程不出现除法，最后求解的时候用线性同余迭代求解，一般题型较多，有的是给定解的范围，求解的数量，例如：PKU 1830、HDU 3364；有的是求一个解，例如PKU 2065、HDU 3571；有的是求解的存在性，例如PKU1288、PKU 3185。

[cpp]view plain copy 
   
 #include<stdio.h>  
 #include<algorithm>  
 #include<iostream>  
 #include<string.h>  
 #include<math.h>  
 using namespace std;  
 const int MOD = 7;  
 const int MAXN = 50;  
 int a[MAXN][MAXN];//增广矩阵  
 int x[MAXN];//解集  
 bool free_x[MAXN];//标记是否是不确定的变元  
 //void Debug()  
 //{  
 //    int i,j;  
 //    for(i = 0;i < equ;i++)  
 //    {  
 //        for(j = 0;j < var+1;j++)  
 //        {  
 //            cout<<a[i][j]<<" ";  
 //        }  
 //        cout<<endl;  
 //    }  
 //    cout<<endl;  
 //}  
 inline int gcd(int a,int b)  
 {  
     int t;  
     while(b!=0)  
     {  
         t = b;  
         b = a%b;  
         a = t;  
     }  
     return a;  
 }  
 inline int lcm(int a,int b)  
 {  
     return a/gcd(a,b)*b;//先除后乘防止溢出  
 }  
 //高斯消元法接方程组。(-2表示有浮点数解,但无整数解,-1表示无解,  
 //0表示唯一解,大于0表示无穷解,并返回自由变元的个数)  
 //有equ个方程,var个变元。增广矩阵行数为equ,分别为0到equ-1,列数为var+1,分别为0到var  
 int Gauss(int equ,int var)  
 {  
     int i,j,k;  
     int max_r;//当前这列绝对值最大的行  
     int col;//当前处理的列  
     int ta,tb;  
     int LCM;  
     int temp;  
     int free_x_num;  
     int free_index;  
   
     for(int i = 0;i <= var;i++)  
     {  
         x[i] = 0;  
         free_x[i] = true;  
     }  
     //转换为阶梯阵  
     col = 0;//处理当前的列  
     for(k = 0;k<equ && col<var;k++,col++)  
     {//枚举当前处理的行,找到该col列元素绝对值最大的那行与第k行交换.(为了在除法时减小误差)  
         max_r = k;  
         for(i = k+1;i < equ;i++)  
         {  
             if(abs(a[i][col]) > abs(a[max_r][col])) max_r = i;  
         }  
         if(max_r!=k)  
         {//与第k行交换  
             for(j = k;j < var+1;j++) swap(a[k][j],a[max_r][j]);  
         }  
         if(a[k][col]==0)  
         {//说明该col列第k行一下全是0了,则处理当前行的下一列  
             k--;  
             continue;  
         }  
         for(i = k+1;i < equ;i++)  
         {//枚举要删去的行  
             if(a[i][col]!=0)  
             {  
                 LCM = lcm(abs(a[i][col]),abs(a[k][col]));  
                 ta = LCM/abs(a[i][col]);  
                 tb = LCM/abs(a[k][col]);  
                 if(a[i][col]*a[k][col] < 0) tb = -tb;//异号的情况是相加  
                 for(j = col;j < var+1;j++)  
                 {  
                     a[i][j] = ((a[i][j]*ta-a[k][j]*tb)%MOD+MOD)%MOD;  
                 }  
             }  
         }  
     }  
     //Debug();  
     //1.无解的情况：化简的增广阵中存在(0,0,...,a)这样的行(a!=0)  
     for(i = k;i < equ;i++)  
     {//对于无穷解来说,如果要判断哪些是自由变元,那么初等行变换中的交换就会影响,则要记录交换  
         if(a[i][col]!=0) return -1;  
     }  
     //2.无穷解的情况：在var*(var+1)的增广阵中出现(0,0,...,0)这样的行,说明没有形成严格的上三角阵  
     //且出现的行数即为自由变元的个数  
     if(k < var)  
     {  
         //首先自由变元有(var-k)个,即不确定的变元至少有(var-k)个  
         for(i = k-1;i>=0;i--)  
         {  
             //第i行一定不会是(0,0,...,0)的情况,因为这样的行是在第k行到第equ行  
             //同样,第i行一定不会是(0,0,...,a),a!=0的情况,这样的无解的  
             free_x_num = 0;//用于判断该行中不确定的变元的合数,如果超过1个,则无法求解,他们仍然为不确定的变元  
             for(j = 0;j < var;j++)  
             {  
                 if(a[i][j]!=0 && free_x[j]) free_x_num++,free_index = j;  
             }  
             if(free_x_num > 1) continue;//无法求解出确定的变元  
             //说明就只有一个不确定的变元free_index,那么可以求解出该变元,且该变元是确定的  
             temp = a[i][var];  
             for(j = 0;j < var;j++)  
             {  
                 if(a[i][j]!=0 && j!= free_index) temp -= a[i][j]*x[j]%MOD;  
                 //temp -= (temp%MOD+MOD)%MOD;  
             }  
             //while(temp%a[i][free_index]!=0) temp+=MOD;  
             x[free_index] = (temp/a[i][free_index])%MOD;//求出该变元  
             free_x[free_index] = 0;//该变元是确定的  
         }  
         return (var-k);//自由变元有(var-k)个  
     }  
     //3.唯一解的情况：在var*(var+1)的增广阵中形成严格的上三角阵  
     //计算出Xn-1,Xn-2,...,X0  
     for(i = var-1;i>=0;i--)  
     {  
         temp = a[i][var];  
         for(j = i+1;j<var;j++)  
         {  
             if(a[i][j]!=0) temp -= a[i][j]*x[j];  
             //temp = (temp%MOD+MOD)%MOD;  
         }  
         //while(temp%a[i][j]!=0) temp+=MOD;  
         //if(temp%a[i][i]!=0) return -2;  
         x[i] = temp/a[i][i];  
     }  
     return 0;  
 }  
 int main()  
 {  
     int i,j;  
     int equ,var;  
     while(scanf("%d %d",&equ,&var)==2)  
     {  
         memset(a,0,sizeof(a));  
         for(i = 0;i < equ;i++)  
         {  
             for(j = 0;j < var+1;j++)  
             {  
                 scanf("%d",&a[i][j]);  
             }  
         }  
         //Debug();  
         int free_num = Gauss(equ,var);  
         if(free_num == -1) printf("No solution\n");  
         else if(free_num == -2) printf("Float but no int solution\n");  
         else if(free_num > 0)  
         {  
             printf("Infinite solution,自由变元个数为%d\n",free_num);  
             for(i = 0;i < var;i++)  
             {  
                 if(free_x[i]) printf("x%d 是不确定的\n",i+1);  
                 else printf("x%d: %d\n",i+1,x[i]);  
             }  
         }  
         else  
         {  
             for(i = 0;i < var;i++)  
             {  
                 printf("x%d: %d\n",i+1,x[i]);  
             }  
         }  
         printf("\n");  
     }  
     return 0;  
 }  