较难推导题(数学+矩阵快速幂)(13长沙邀请赛)(4565)

So Easy!

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 3499    Accepted Submission(s): 1129

Problem Description

　　A sequence S _n is defined as:

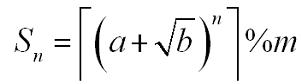
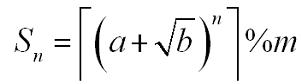
Where a, b, n, m are positive integers.┌x┐is the ceil of x. For example, ┌3.14┐=4. You are to calculate S _n.
　　You, a top coder, say: So easy!

 

Input

　　There are several test cases, each test case in one line contains four positive integers: a, b, n, m. Where 0< a, m < 2 ¹⁵, (a-1) ²< b < a ², 0 < b, n < 2 ³¹.The input will finish with the end of file.

 

Output

　　For each the case, output an integer S _n.

 

Sample Input

  

   2 3 1 2013
2 3 2 2013
2 2 1 2013
  

 

Sample Output

  

   4
14
4
  

 

Source

2013 ACM-ICPC长沙赛区全国邀请赛——题目重现 

Sn=⌈(a+b√)n⌉%m,(a−1)2<b<a2

这个题目也是2008年Google Codejam Round 1A的C题。

做法其实非常简单，记 (a+b√)n 为 An ，配项

Cn=An+Bn=(a+b√)n+(a−b√)n

两项恰好共轭，所以 Cn 是整数。又根据限制条件

(a−1)2<b<a2⇒0<a−b√<1⇒0<(a−b√)n<1⇒Bn<1

也就是说 Cn=⌈An⌉

Sn=(Cn)%m

求 Cn 的方法是递推。 对 Cn 乘以 (a+b√)+(a−b√)

于是

Cn+1=2aCn−(a2−b)Cn−1

把这个递推式写成矩阵形式

[Cn+1Cn]=[2a1−(a2−b)0][CnCn−1]

于是就可以用矩阵快速幂来做了

[Cn+1Cn]=[2a1−(a2−b)0]n[C1C0]

题目的解法的构造一个共轭项，从而可以化简，递推过程难度比较大，很难想到。下面是基本思路：

①得到Cn是整数；②得到Bn的范围；③化简原式用Cn表示Sn；④求Cn得递推式；⑤用矩阵构造递推式然后用矩阵快速幂求Cn。取模过程还需要小心：因为有很大可能是减法操作，所以需要+m然后再%m。

/*------------------Header Files------------------*/
#include <iostream>
#include <cstring>
#include <string>
#include <cstdio>
#include <algorithm>
#include <cstdlib>
#include <ctype.h>
#include <cmath>
#include <stack>
#include <queue>
#include <deque>
#include <map>
#include <vector>
#include <limits.h>
using namespace std;
/*------------------Definitions-------------------*/
#define LL long long
#define uLL unsigned long long
#define PI acos(-1.0)
#define INF 0x3F3F3F3F
#define MOD 9973
#define MAX 500050
#define lson rt<<1,l,m
#define rson rt<<1|1,m+1,r
/*---------------------Work-----------------------*/
LL m;
struct node
{
	LL num[3][3];
};
node ans,res;
node multi(node a,node b)
{
	node c;
	memset(c.num,0,sizeof(c.num)); //不要忘记初始化
	for(int i=1;i<=2;i++)
	{
		for(int k=1;k<=2;k++)
		{
			if(a.num[i][k]==0) continue;
			for(int j=1;j<=2;j++)
				c.num[i][j]=(c.num[i][j]+a.num[i][k]*b.num[k][j]+m)%m;
		}
	}
	return c;
}
void matrix(LL n)
{
	while(n)
	{
		if(n&1) res=multi(res,ans);
		ans=multi(ans,ans);
		n>>=1;
	}
}
void work()
{
	LL a,b,n;
	while(scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&m)==4)
	{
		if(n==1)
		{
			cout<<2*a%m<<endl;
			continue;
		}
		ans.num[1][1]=2*a,ans.num[1][2]=b-a*a;
		ans.num[2][1]=1,ans.num[2][2]=0;
		res.num[1][1]=res.num[2][2]=1; //单位矩阵
		res.num[1][2]=res.num[2][1]=0;
		matrix(n-1);
		printf("%I64d\n",((res.num[1][1]*2*a+res.num[1][2]*2)%m+m)%m);
	}
}
/*------------------Main Function------------------*/
int main()
{
	//freopen("test.txt","r",stdin);
	//freopen("cowtour.out","w",stdout);
	//freopen("cowtour.in","r",stdin);
	work();
	return 0;
}