kaggle小白入门——泰坦尼克号公分0.8+

经过不断的尝试，看了无数的kernels以及各种博客，终于把公分提到了0.8以上，写这篇博客记录一下，也希望能够对各位新手们有所帮助。

一、导包

# 数据处理及可视化
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 算法
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVC
# 训练
from sklearn.model_selection import train_test_split
from sklearn.model_selection import learning_curve
from sklearn.model_selection import ShuffleSplit
from sklearn.model_selection import GridSearchCV

二、获取数据

train = pd.read_csv("all/train.csv")
test = pd.read_csv("all/test.csv")
gender_submission = pd.read_csv("all/gender_submission.csv")

三、数据分析及特征工程

train.describe(include="all")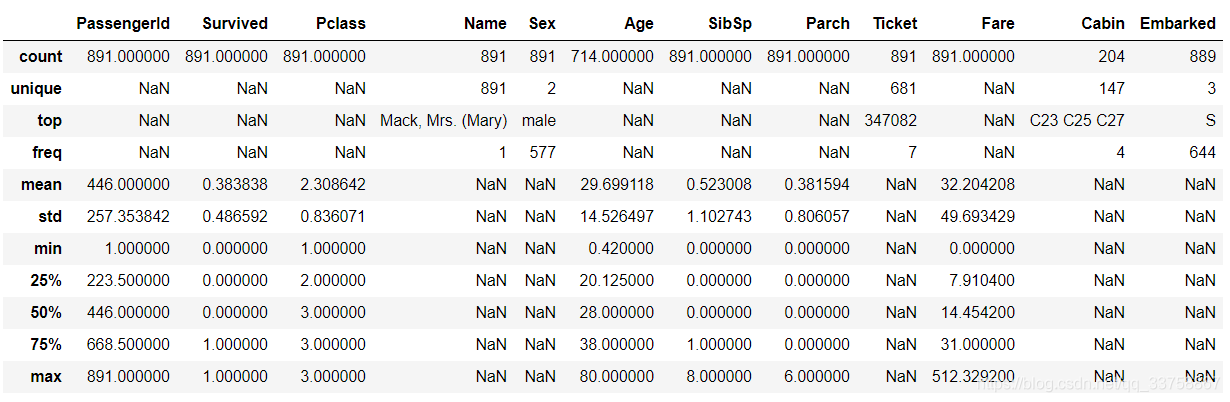

各个特征总结：

PassengerId：当然没用；

Pclass：代表社会地位，社会地位越高，当然越容易存活；

Name：初次尝试时，多数人会把Name直接删掉。但后面越来越深入，会发现Name中隐含着巨大的信息，包括称呼，姓氏。也有见过使用名字长度为特征的，我也尝试了一下，发现并没有太大的帮助；

Sex：女士优先原则，女性的生存率相当的高；

Age：小孩生存率相当高。年龄有大量缺失值，需要填充；

SibSp：船上的兄弟姐妹和配偶数量；

Parch：船上的父母子女数量；

Ticket：初次尝试时，也都会把Ticket去掉。但是，Ticket与Name一起构成了重要的家庭特征，也是本文大力处理的地方；

Fare：票价与票号对应，相同票号价格相同，但相同票价不一定相同票号；

Cabin：多数用有无Cabin特征处理，但其实影响不大；

Embarked：S港登船的人最多，生存率也最高，但经过尝试，其实影响也不大。

对于Cabin,Embarked等已经在我的模型中可有可无的特征，本文将不再讨论。本文重点将在Name,SibSp,Parch,Ticket中讨论，来构建家庭和团体特征。

Sex生存率：

sns.barplot(x="Sex", y="Survived", data=train)
print("女性生存率:", train["Survived"][train["Sex"] == "female"].value_counts(normalize=True)[1])
print("男性生存率:", train["Survived"][train["Sex"] == "male"].value_counts(normalize=True)[1])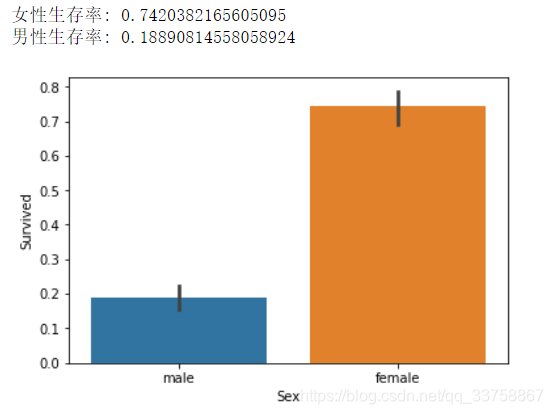

可以看到，女性生存率相当的高，男性生存率相当的低。基本上每5个女性有1个死亡，每5个男性有1个存活，这里就要注意了，假设泰坦尼克上女的全活了，男的全死了，那么我们就需要关注一下那个死亡的女性发生了什么恐怖的事，以及那个活着的男性遇到了什么幸运的事。纵观特征，唯一能够想到的就是各种亲友拖累了那个死亡的女性或者救了那个活着的男性，因此将注意力转到家庭以及同行的人。（其实是看各种大佬kernels得到的启发）

添加Family_size特征

train["Family_size"] = train["SibSp"] + train["Parch"]
test["Family_size"] = test["SibSp"] + test["Parch"]

添加Fname特征，即姓氏

train["Fname"] = train.Name.apply(lambda x: x.split(",")[0])
test["Fname"] = test.Name.apply(lambda x: x.split(",")[0])

然后，经过一系列的爆炸观察，好吧，这里没有可视化，就是一条一条数据直接肉眼观察的。

结论：

1、Fname相同，Ticket相同，Family_size>0可以确定一个家庭，只有一个家庭例外，这个家庭的票号连号，但影响不大。

2、有女性死亡的家庭，除了1岁以下的婴儿外，家庭成员全部死亡。（分数第一次有大的提升，也是添加了该特征之后）

3、家庭中若有大于18岁男性存活，或年龄为nan的男性存活，则该家庭全部存活。（加入该特征后，公分达到了0.8）

4、其余家庭，除极个别