基于Python 利用桑基图（Sankeydiagram）表示转移矩阵（土地利用）

桑基图桑，基能量分流图，也叫桑基能量平衡图。它是一种特定类型的流程图，图中延伸的分支的宽度对应数据流量的大小，通常应用于能源、材料成分、金融等数据的可视化分析。因1898年Matthew Henry Phineas Riall Sankey绘制的“蒸汽机的能源效率图”而闻名，此后便以其名字命名为“桑基图”。

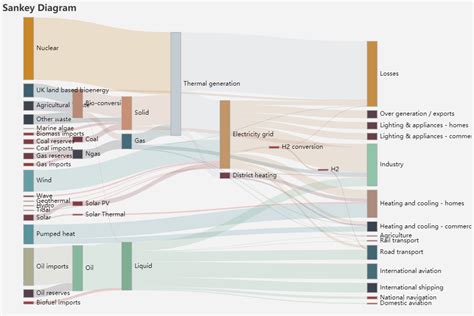
看到这么炫酷的图，是不是心动了呢 

对于土地利用文献中大多使用转移矩阵的方式。本博客实现2000年，2005年，2010年，2015年，2019年土地利用之间的转移情况使用桑基图可视化。

首选，这里土地利用与编号对应如下：

1	2	3	4	5	6	7	8	9
Forest	Grassland	Grassland	Cultivated Land	Artifical Surface	Water Body	Wetland	Snow and Ice	Bare Land

 

使用栅格计算器工具基于2000.tif,2005.tif,2010.tif,2015.tif,2019.tif。四期数据，计算五期数据的转移情况，

公式如下：

10000*2000.tif+1000*2005.tif+100*2010.tif+10*2015.tif+2019.tif.。

得到栅格数据即为转移情况，将栅格数据的属性表导出到本地，如下，其中，11113表示2000，2005，2010，2015是1，2019是3。

笔者在后面添加十个表头，如下。将Value值拆分，分别赋值给a1-a5,name1-name5用于存储五期数据土地利用名字，如Forest(2000),Forest(2005)等

读者可以将数据做成如上格式，首选进行Value值的拆分和赋值

import pandas as pd

path=r'D:\study\tmp'
import os
os.chdir(path)
name='2000_2005_2010_2015_2019.csv'
#name='sankey - 副本.csv'
df=pd.read_csv(name)
df['a1']=df['Value']//10000
df['a2']=(df['Value']-df['a1']*10000)//1000
df['a3']=(df['Value']-df['a1']*10000-df['a2']*1000)//100
df['a4']=(df['Value']-df['a1']*10000-df['a2']*1000-df['a3']*100)//10
df['a5']=df['Value']-df['a1']*10000-df['a2']*1000-df['a3']*100-df['a4']*10

name2000=['Forest(2000)','Grassland(2000)','Shrubland(2000)','Cultivated Land(2000)','Artifical Surface(20000)',
      'Water Body(2000)','Wetland(2000)','Snow and Ice(2000)','Bare Land(2000)']

name2005=['Forest(2005)','Grassland(2005)','Shrubland(2005)','Cultivated Land(2005)','Artifical Surface(2005)',
      'Water Body(2005)','Wetland(2005)','Snow and Ice(2005)','Bare Land(2005)']

name2010=['Forest(2010)','Grassland(2010)','Shrubland(2010)','Cultivated Land(2010)','Artifical Surface(2010)',
      'Water Body(2010)','Wetland(2010)','Snow and Ice(2010)','Bare Land(2010)']

name2015=['Forest(2015)','Grassland(2015)','Shrubland(2015)','Cultivated Land(2015)','Artifical Surface(2015)',
      'Water Body(2015)','Wetland(2015)','Snow and Ice(2015)','Bare Land(2015)']

name2019=['Forest(2019)','Grassland(2019)','Shrubland(2019)','Cultivated Land(2019)','Artifical Surface(2019)',
      'Water Body(2019)','Wetland(2019)','Snow and Ice(2019)','Bare Land(2019)']
import numpy as np
b1=np.array(df['a1'])
b2=np.array(df['a2'])
b3=np.array(df['a3'])
b4=np.array(df['a4'])
b5=np.array(df['a5'])

def f(b,name):
    re=[]
    for i in range(len(b)):
        #print(b[i])
        re.append(name[b[i]])
        
    return re
        
        

n1=f(b1,name2000)
n2=f(b2,name2005)
n3=f(b3,name2010)
n4=f(b4,name2015)
n5=f(b5,name2019)
df['name1']=n1
df['name2']=n2
df['name3']=n3
df['name4']=n4
df['name5']=n5
df.to_csv('re.csv')

处理后的结果如下：

然后我们将Value,a1,a2,a3,a4,a5,列删除，当然也可以在用Pandas读取时，只读取这几行。笔者采取直接删除的方式，

 

下面我们将数据进行预处理，处理成Sankey绘图需要的格式，生成nodes 和linkes

from pyecharts import options as opts
from pyecharts.charts import Sankey
import pandas as pd

import os
path=r'D:\study\tmp'
os.chdir(path)
name='sankey.csv'
name='re1.csv'
#name='sankey - 副本.csv'
df=pd.read_csv(name)
nodes=[]
for i in range(5):
    values=df.iloc[:,i].unique()
    for value in values:
        #print(value)
        dic={}
        dic['name']=value
        nodes.append(dic)
        
print(nodes)

f1=df.groupby(['name1','name2'])['Count'].sum().reset_index()
f2=df.groupby(['name2','name3'])['Count'].sum().reset_index()
f3=df.groupby(['name3','name4'])['Count'].sum().reset_index()
f4=df.groupby(['name4','name5'])['Count'].sum().reset_index()

f1.columns=['source','target','value']
f2.columns=['source','target','value']
f3.columns=['source','target','value']
f4.columns=['source','target','value']
result=pd.concat([f1,f2,f3,f4])




linkes=[]
for i in result.values:
    dic={}
    dic['source']=i[0]
    dic['target']=i[1]
    dic['value']=i[2]
    linkes.append(dic)
print(linkes)

nodes的结果如下：

linkes的结果如下：形式为source-target-value

最后绘制桑吉图

from pyecharts.charts import Sankey
from pyecharts import options as opts
 
 
pic = (
    Sankey()
    .add('',
         nodes,
         linkes,
         linestyle_opt=opts.LineStyleOpts(opacity = 0.3, curve = 0.5, color = 'source'),
         label_opts=opts.LabelOpts(position = 'top'),
         node_gap = 30,
    )
    .set_global_opts(title_opts=opts.TitleOpts(title = ''))
)

 
 
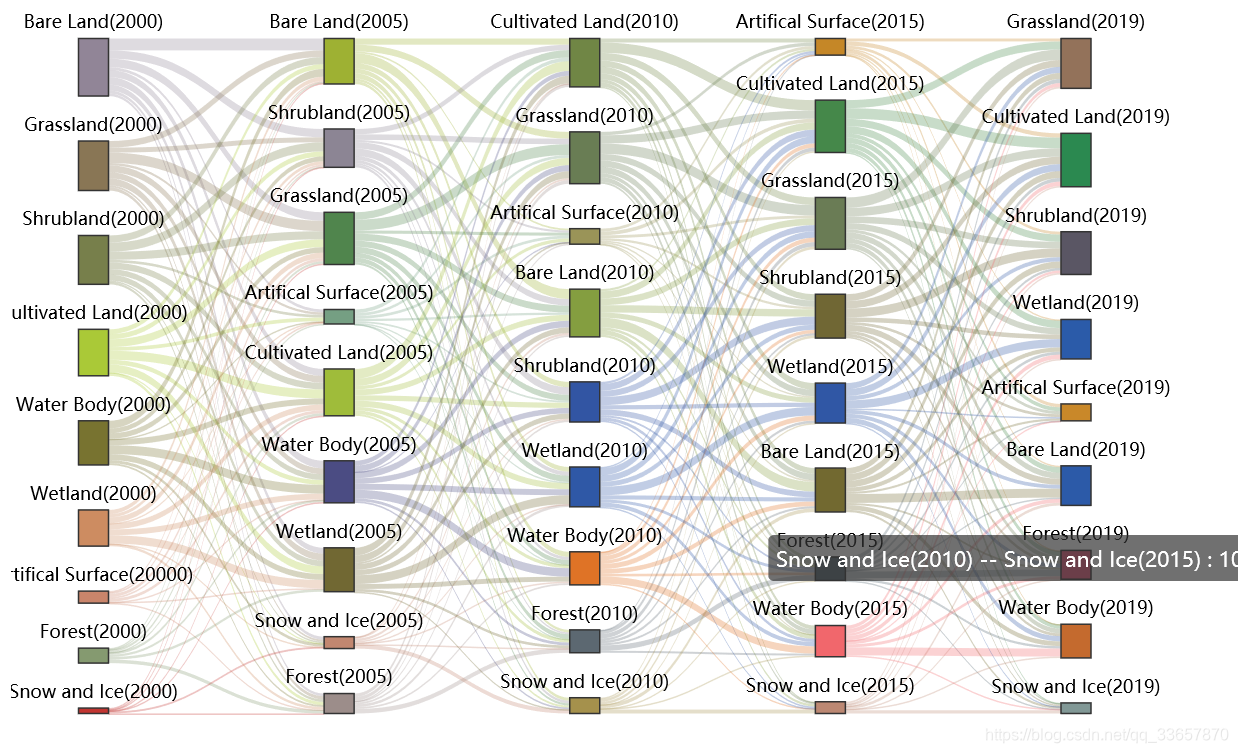
pic.render('2000_2005_2010_2015_2019.html')

打开html文件，结果如下：