机器学习实战之K-邻近算法代码笔记

最新推荐文章于 2024-04-20 19:30:30 发布

原创最新推荐文章于 2024-04-20 19:30:30 发布 · 199 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#机器学习 #监督算法

机器学习专栏收录该内容

1 篇文章

订阅专栏

本文深入探讨K-邻近算法的工作原理，包括计算距离、排序、选择最近邻及分类决策过程。通过约会网站数据实例，展示了算法在数据预处理、特征选择、归一化处理及效果测试的应用。

第2章 K-邻近算法
此算法根据待测点与已知分类点的距离来确定新数据点的分类，通过比较计算的距离，选择距离靠近的前K个分类点。最后选出这K个分类点中频率最高的类别作为待测点的类别。
该算法的伪代码如下：
（1）计算已知类别数据集中的点与当前点之间的距离
（2）按照距离递增次序排序
（3）选取与当前距离最小的K个点
（4）确定前K个点所在类别的出现评率
（5）返回前K个点出现频率最高的类别作为当前点的预测分类

下面根据一个约会网站的例子来了解K-邻近算法
该数据文本共有1000行，主要包括了以下三个特征：

每年获得的飞行常客里程数	玩视频游戏所耗时间百分比	每周消费的冰淇淋公升数	类别标签
40920	8.326976	0.953952	3

下面开始在代码上观测
1、读取数据


'''
此片段代码为读取数据并修改数据格式为可用格式
'''
from numpy import *
import operator
from os import listdir
def file2matrix(filename):
    fr = open(filename)
    numberOfLines = len(fr.readlines())         #计算数据集的行数 （1000）
    returnMat = zeros((numberOfLines,3))        #创建一个全零的[1000x3]数组
    classLabelVector = []                       #准备一个空列表，用来放置类别标签
    fr = open(filename)
    index = 0
    for line in fr.readlines():
        line = line.strip()                    
        listFromLine = line.split('\t')         
        returnMat[index,:] = listFromLine[0:3]  #获取数据的前三列内容（[4.092000e+04 8.326976e+00 9.539520e-01]）
        classLabelVector.append(int(listFromLine[-1])) #获取数据最后一列的类别标签并放在classLabelVector中（[3, 2, 1, 1,...]）
        index += 1
    return returnMat,classLabelVector

以上已经将数据内容放在returnMat中，标签类别放在classLabelVector中
可以使用Matplotlib制作出散点图来观察数据分布
2、观测数据

import matplotlib
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure(1)
ax = fig.add_subplot(111)
ax1 = plt.subplot(2,1,2)
ax2 = plt.subplot(2,2,1)
ax3 = plt.subplot(2,2,2)
plt.sca(ax1)
plt.sca(ax2)
plt.sca(ax3)
ax1.scatter(datingDatasMat[:,0],datingDatasMat[:,1],15.0*array(classLabelVector),15.0*array(classLabelVector)) #第零列与第一列比较
ax2.scatter(datingDatasMat[:,1],datingDatasMat[:,2],15.0*array(classLabelVector),15.0*array(classLabelVector)) #第一列与第二列比较
ax3.scatter(datingDatasMat[:,0],datingDatasMat[:,2],15.0*array(classLabelVector),15.0*array(classLabelVector)) #第零列与第二列比较
plt.show()

结果如下：
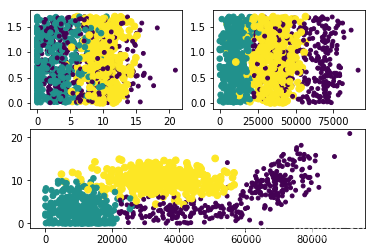
在这里插入图片描述
从上图可以看出第一列和第二列的展示效果最好，也就是飞行常客里程数与玩视频游戏所占百分比更容易区分想要约会的人群
由于K-邻近算法要获取的是数据点之间的距离，不同数量级的数据所造成的结果影响非常之大，所以需要将数据统一在一个数量级中做计算。也就是要对数据做归一化处理。
3、归一化处理

def autoNorm(dataSet):
    minVals = dataSet.min(0)     #获取每列的最小值（[0.       0.       0.001156]）
    maxVals = dataSet.max(0)     #获取每列的最大值（[9.1273000e+04 2.0919349e+01 1.6955170e+00]）
    ranges = maxVals - minVals   #归一化分母
    normDataSet = zeros(shape(dataSet))  #创建全零数组
    m = dataSet.shape[0]                 #得到行数
    normDataSet = dataSet - tile(minVals, (m,1))   #对应的位置相减得到分子
    print(tile(minVals, (m,1)) )
    normDataSet = normDataSet/tile(ranges, (m,1))   #归一化后的数据
    return normDataSet, ranges, minVals

数据已被归一化完成，数据在0~1之间。下面将数据使用K-邻近算法处理。
4、测试K-邻近算法效果

def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0]   #获取行数
    diffMat = tile(inX, (dataSetSize,1)) - dataSet  #输入数据与已知所有数据相减
    sqDiffMat = diffMat**2    #算出了到每个数据的距离的平方
    sqDistances = sqDiffMat.sum(axis=1)  #对数据按行求和
    distances = sqDistances**0.5       #获得K邻近算法的距离值
    sortedDistIndicies = distances.argsort()     #获取值从小到大的下标值
    classCount={}          
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]  #获取对应的标签值
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1      #相应类别计数
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)   #将计数的值排序
    return sortedClassCount[0][0]   #获得排名最高的类别

上面程序最后会得到出现频率最高的标签作为新数据的标签

def datingClassTest():
    hoRatio = 0.1      #测试数据占10%
    datingDataMat,datingLabels = file2matrix("testfile.txt")       #load data setfrom file
    normMat, ranges, minVals = autoNorm(datingDataMat) #归一化的结果
    m = normMat.shape[0]
    numTestVecs = int(m*hoRatio) #测试数据行数
    errorCount = 0.0  #初始化错误率
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        #print ("the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i]))
        if (classifierResult != datingLabels[i]): errorCount += 1.0    #判断结果是否正确
    print ("the total error rate is: %f" % (errorCount/float(numTestVecs)))
    print (errorCount)