私房菜数据结构和算法--图

一、图的定义和分类

定义：图是由一组顶点和一组能够将两个顶点相连的边组成。

特殊的图：自己连自己的（自环）；两个顶点多条线相连（平行边）

图的分类：有向图（边不仅有连接作用，且有方向）、无向图（边仅仅做连接作用）

二、无向图

相关术语

• 相邻顶点：一条边连接的两个顶点，且这条边依附于这个顶点
• 度：某个顶点的度就是依附于这个顶点的边的个数
• 子图：是一幅图的所有边的子集(包含这些边依附的顶点)组成的图
• 路径：由边顺序连接的一系列的顶点组成
• 环：一条至少含有一条边且终点和起点相同的路径
• 连通图：如果图中任意一个顶点都存在一条路径到达另外一个顶点，那么这幅图就称之为连通图
• 联通子图：一个非连通图由若干连通的部分组成，每一个连通的部分都可以称为该图的连通子图

存储结构

邻接矩阵：有n*n的数组组成，把索引的值看作顶点，如果两个节点相连，则(a,b)和(b,a)的值设为1，否则设为0

邻接表：由一个元素是队列的数组组成，元素的索引是节点的值，队列里的值代表和当前节点相连的节点

三、图的搜索

深度优先：在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找子结点，然后找兄弟结点

广度优先：在搜索时，如果遇到一个结点既有子结点，又有兄弟结点，那么先找兄弟结点，然后找子结点

四、有向图

有向图是一幅有方向性的图，是由一组顶点和一组有方向的边组成的，每条方向的边都连着一对有序的顶点。

• 出度：由某个顶点指出的边的个数称为该顶点的出度
• 入度：指向某个顶点的边的个数称为该顶点的入度
• 有向路径：由一系列顶点组成，对于其中的每个顶点都存在一条有向边，从它指向序列中的下一个顶点
• 有向环：一条至少含有一条边，且起点和终点相同的有向路径

有向环检测：

添加了onStack[] 布尔数组，索引为图的顶点，当我们深度搜索时：

• 如果当前顶点正在搜索，则把对应的onStack数组中的值改为true，标识进栈
• 如果当前顶点搜索完毕，则把对应的onStack数组中的值改为false，标识出栈
• 如果果即将要搜索某个顶点，但该顶点已经在栈中，则图中有环

顶点排序：

添加了一个栈reversePost用来存储顶点，当我们深度搜索图时，每搜索完毕一个顶点，把该顶点放入到reversePost中，这样就可以实现顶点排序。

五、最小生成树

定义：图的生成树是它的一棵含有其所有顶点的无环连通子图，一副加权无向图的最小生成树它的一棵权值(树中所有边的权重之和)最小的生成树

约定：只考虑连通图。最小生成树的定义说明它只能存在于连通图中，如果图不是连通的，那么分别计算每个连通图子图的最小生成树，合并到一起称为最小生成森林。

最小生成树原理：①任意两个节点相连都会生成一个环；②任意删一边，都会生成两颗树

切分原理

• 切分：将图的所有顶点按照某些规则分为两个非空且没有交集的集合
• 横切边：连接两个属于不同集合的顶点的边称之为横切边

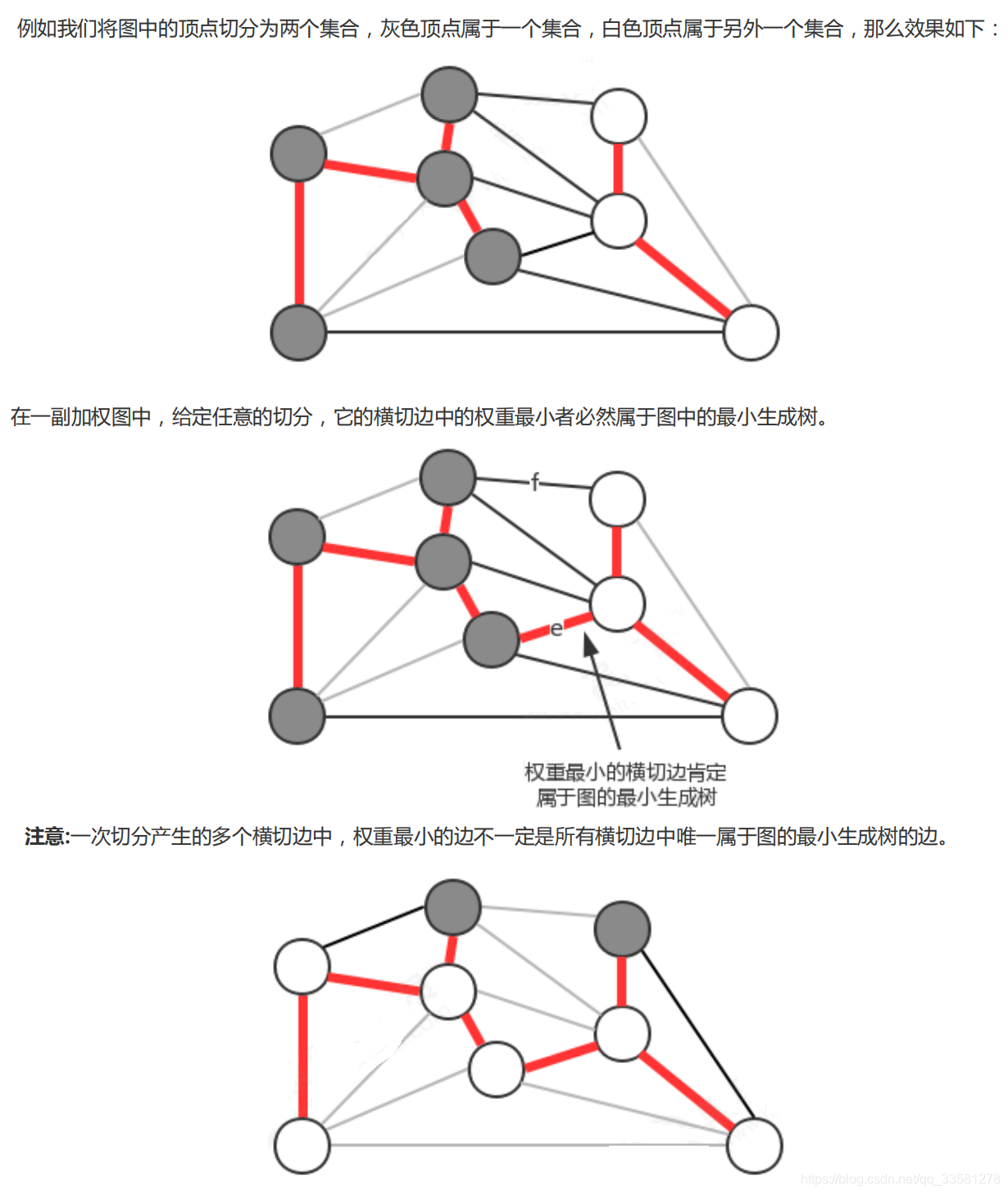
贪心算法：使用切分定理找到最小生成树的一条边，不断的重复直到找到最小生成树的所有边（一直切两份直到最小生成树生成）

prim算法：把最小生成树中的顶点看做是一个集合，把不在最小生成树中的顶点看做是另外一个集合

kruskal算法：借助一个MinPriorityQueue pq存储图中所有的边，取权重最小的边，判断连接该边的两个点，判断两个点是否联通，如果联通则不能加入树中，如果没联通则加入树中