奇怪汉诺塔笔记

奇怪的汉诺塔

普通的汉诺塔问题

问题解释：

借助B将A上面的圆盘串到C上面，大的圆盘不能放小的圆盘上面。每次只能移动一块圆盘。怎么样移动才能完成任务？

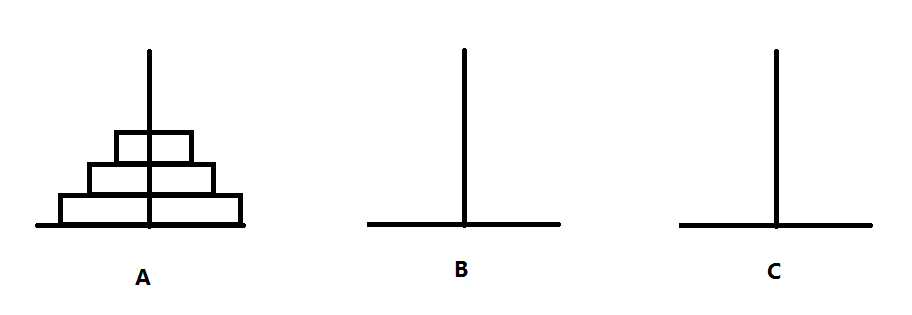
思路分析：

1. 最简单的情况：

   当A上面的圆盘只有一块的时候：直接将A上面的圆盘放到C上面即可

   A——>C

2. 其次：

   当圆盘数量等于2的时候：将第一个圆盘放到B上面，再将A上面最底下的圆盘放到C上，再将B上面的圆盘放到C上

   A——>B

   A——>C

   B——>C

3. 可以推出，当圆盘数为n的时候：

   • 第一步：先将A上面n-1个盘子放到B

   • 第二步：再将A上面剩下的一个盘子放到C

   

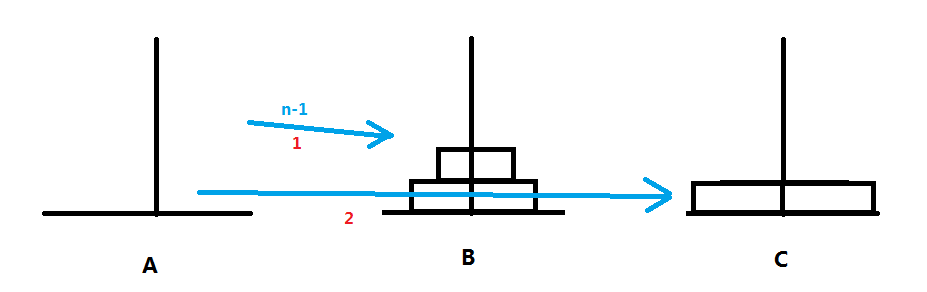
   • 第三步：最后将B上面的n-1的盘子放到C。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BViWngLa-1585226429360)(https://images.21hut.com/typora/20200317222037-720637.png)]

代码解释：

work是递归函数：

参数1： begin指从哪根柱子上移动盘子

参数2： help 指借助哪根柱子

参数3： reach 指将盘子移动到哪根柱子上面

参数4： num 指一次移动多少个盘子

代码：

#include<stdio.h>

void work(char begin,char help,char reach,int num){
    //如果只剩下一个盘子，就直接拿（没什么好说的）
	if(num == 1) {
		printf("%c --> %c\n",begin,reach);
		return;
	}
	
    //分成三步：
    //第一步：将n-1个盘子移动到借助的柱子上面
	work(begin,reach,help,num-1);
    //第二步：将剩下的那一个盘子，移动到最终要到达的柱子上面
	printf("%c --> %c\n",begin,reach);
    //第三步：将最后的n-1个盘子从借助的柱子上移动到最终要到达的柱子上面
	work(help,begin,reach,num-1);
}


int main(){
	
	work('A','B','C',3);
	return 0;
}

奇怪的汉诺塔

题目地址：

https://www.acwing.com/problem/content/98/

题目简介：

汉诺塔问题，条件如下：

1、这里有A、B、C和D四座塔。

2、这里有n个圆盘，n的数量是恒定的。

3、每个圆盘的尺寸都不相同。

4、所有的圆盘在开始时都堆叠在塔A上，且圆盘尺寸从塔顶到塔底逐渐增大。

5、我们需要将所有的圆盘都从塔A转移到塔D上。

6、每次可以移动一个圆盘，当塔为空塔或者塔顶圆盘尺寸大于被移动圆盘时，可将圆盘移至这座塔上。

请你求出将所有圆盘从塔A移动到塔D，所需的最小移动次数是多少。

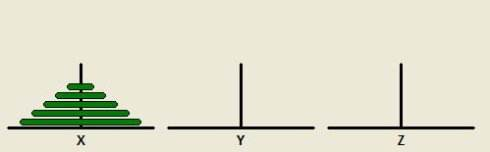
汉诺塔塔参考模型

输入格式

没有输入

输出格式

对于每一个整数n(1≤n≤121≤n≤12),输出一个满足条件的最小移动次数，每个结果占一行。

输入样例：

没有输入

输出样例：

参考输出格式

题目分析：

这个跟普通的汉诺塔的区别;

普通的汉诺塔的可使用的柱子只有3根，这里的柱子有4根。这意味着什么呢，原本我们只能借助3根柱子帮忙移动盘子，现在多出来一根柱子就多出来一个空间，就会使我们操作的次数减少。

这样我们的操作就会变成如下：

• 第一步：将随意的盘子（i）放到第四根柱子上面

放置的盘子数量不同会影响最终的操作次数，所以要对其遍历，取操作次数最小的那种情况

• 第二步：将剩下盘子（n - i）中的（n-i-1）个盘子放到第二根柱子上面

接下来对（n-i）个盘子的操作跟普通的汉诺塔操作一致

• 第三步：将剩余的一个盘子放到第三根（最后要到达的位置）上面

• 第四步：将第二根上面的盘子（n-i-1）个盘子放到第三根柱子上面

• 第五步：将第四根柱子上面的盘子放到第三根柱子上面

代码解释：

使用递推：

数组dp1[15]:用于记录普通汉诺塔转移1-15个盘子分别需要的操作次数;

数组f[15]：记录奇怪的汉诺塔转移1-15个盘子分别需要的操作次数;

看代码注释

代码：

#include<iostream>
#include<cstring>
using namespace std;

int main(){
	
	int dp1[15]={0};
	int f[15];
	memset(f,0x3f,sizeof(f));
    //没有盘子就操作为0
	f[0] = 0;
    //当只有一个盘子的时候操作数为1
	dp1[1] = 1;
    
	for(int i = 2; i < 15;i++){
        //分三步，第一步转移i-1个盘子，第二步转移1个，第三步i-1个盘子
        //每次转移都要进行三步，所以将三步相加便是当前转移的操作数
		dp1[i] = dp1[i-1]+1+dp1[i-1];
	}
	
	for(int i = 1; i <= 12; i++){
        //遍历放到第四个柱子上面的盘子数：不同的盘子数总体需要操作的次数也不同
		for(int j = 0; j < i; j++){
            //min：取遍历中操作次数最少的
            //第一步根第五步：都移动了j个盘子，操作次数*2
            //第二步到第四步：剩下的盘子，由于第四根柱子已经被使用了，所以操作跟普通的汉诺塔一样 
            //注意：第一步跟第五步可以借用的柱子数时四根，所以要使用f数组，而第二步到第四步由于只能借助三根所以使用数组dp1;
			f[i] = min(f[i],f[j]*2+dp1[i-j]);
		}
		cout<<f[i]<<endl;
	}
	return 0;
}

子，由于第四根柱子已经被使用了，所以操作跟普通的汉诺塔一样
//注意：第一步跟第五步可以借用的柱子数时四根，所以要使用f数组，而第二步到第四步由于只能借助三根所以使用数组dp1;
f[i] = min(f[i],f[j]*2+dp1[i-j]);
}
cout<<f[i]<<endl;
}
return 0;
}