（六省）蓝桥真题 垒骰子

垒骰子

赌圣atm晚年迷恋上了垒骰子，就是把骰子一个垒在另一个上边，不能歪歪扭扭，要垒成方柱体。
经过长期观察，atm 发现了稳定骰子的奥秘：有些数字的面贴着会互相排斥！

我们先来规范一下骰子：1 的对面是 4，2 的对面是 5，3 的对面是 6。

假设有 m 组互斥现象，每组中的那两个数字的面紧贴在一起，骰子就不能稳定的垒起来。 
atm想计算一下有多少种不同的可能的垒骰子方式。
两种垒骰子方式相同，当且仅当这两种方式中对应高度的骰子的对应数字的朝向都相同。
由于方案数可能过多，请输出模 10^9 + 7 的结果。

不要小看了 atm 的骰子数量哦～

「输入格式」
第一行两个整数 n m
n表示骰子数目
接下来 m 行，每行两个整数 a b ，表示 a 和 b 数字不能紧贴在一起。

「输出格式」
一行一个数，表示答案模 10^9 + 7 的结果。

「样例输入」
2 1
1 2

「样例输出」
544

「数据范围」
对于 30% 的数据：n <= 5
对于 60% 的数据：n <= 100
对于 100% 的数据：0 < n <= 10^9, m <= 36

资源约定：
峰值内存消耗 < 256M
CPU消耗  < 2000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

分析：

递推方法：

用表示垒了个骰子，且最上面的骰子顶面是。递推式为 ，表示和不冲突的情况。

骰子有明确的对立面（1,4）（2,5）（3,6），可声明一维数组op[7] = {0,4,5,6,1,2,3}来存储，op[x]表示“x”面的对立面。

垒骰子时存在互斥面，需要程序运行时输入。可声明二维数组（矩阵）来存储。当互斥面是1,2时，Matrix[7][7]如下，矩阵外的一行对应的是顶面数字。

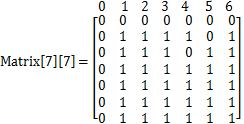
Matrix[i][j]表示n-1层骰子顶面为i数字，第n层顶面是j数字是否互斥，互斥为0，否则为1。

即Matrix[1][ op[2] ] = Matrix[2][ op[1] ] = 0，这样在矩阵相乘时，不会使计数加一。

最终的种类数，即

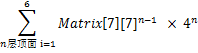
 为方便计算，声明一维数组 d[] = {0,1,1,1,1,1,1,} ，计算总个数。规律如下：

当n = 1时，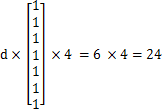     

当n = 2时，    

当n = 3时，    

...

第n层，          

最终结果        

 此种方法叫做：矩阵快速幂。借鉴：https://www.cnblogs.com/565261641-fzh/p/8515633.html

#include <iostream>
#include <cstring>
#include <vector> 
#define MOD 1000000007 
using namespace std; 
/* run this program using the console pauser or add your own getch, system("pause") or input loop */

typedef vector<vector<int> > Mat; //定义基本数据类型 
const int op[7] = {0,4,5,6,1,2,3}; //定义骰子的对立面 
int d[7] = {0,1,1,1,1,1,1};
//两个矩阵相乘  
Mat mul(Mat & a, Mat & b)
{
	Mat t;
	t.resize(7);//临时矩阵 
	int multi = 0;//记录i行j列对应项相乘的和 
	for(int i = 0; i < 7; i++)
	{
		for(int j = 0; j < 7; j++)
		{
			multi = 0;
			for(int k = 0; k < 7; k++)
				multi += (a[i][k] * b[k][j])%MOD;	
			t[i].push_back(multi);
		}
	}
	return t;
}
// 向量和矩阵相乘 
int mul_d(Mat &a)
{
	int temp= 0;
	int multi = 0;
	for(int j = 0;j < 7; j++)
	{
		multi = 0;
		for(int k = 0; k < 7; k++)
			multi += (d[k] * a[k][j])%MOD;	
		temp  = (temp + multi)%MOD;
		cout<<temp<<endl; 
	}
	return temp;
}
//输出矩阵mat
void print_mat(Mat mat)
{
	for(int i = 0; i < 7; i++)
	{
		for(int j = 0; j < 7; j++)
		{
			cout<<mat[i][j]<<" ";
		}
		cout<<endl;
	 } 
	 cout<<endl;
} 
int main(int argc, char** argv) {
	Mat mat;
	mat.resize(7);
	//0行0列初始化为0
	for(int i = 0; i < 7; i++)
	{
		mat[i].push_back(0);
		mat[0].push_back(0);
	} 
	//1~6行/列 初始化为1 
	for(int i = 1; i < 7; i++)
	{
		for(int j = 1; j < 7; j++)
		{
			mat[i].push_back(1); 
		}
	}
	//输入骰子数和互斥对数 
	int n,m;
	cin>>n>>m;
	//逐行输入互斥对，完善互斥矩阵 
	int a,b; 
	for(int i = 0; i < m; i++)
	{
		cin>>a>>b;
		mat[a][op[b]] = 0;
		mat[b][op[a]] = 0; 
	}
	cout<<"mat = "<<endl;
	print_mat(mat);
	//声明并初始化为单位矩阵 
	Mat t;
    t.resize(7);
    for(int i = 0; i < 7; i++)
    {
    	for(int j = 0; j < 7; j++)
    	{
    		if(i == j) t[i].push_back(1);
			else t[i].push_back(0);
		}
	}
	cout<<"t= "<<endl;
	print_mat(t);
	//求变换矩阵的n-1次方 
	int beishu = 4;
    while(n > 1)
    {
    	t = mul(t,mat);
    	beishu *= 4;
    	n--;
	}
	cout<<"n-1次连乘之后 t="<<endl;
	print_mat(t);
	//情况总数ans = d[] * m的n-1次方 * 4的n次方 
	int ans = mul_d(t) * beishu;
	cout<<"ans = "<<ans<<endl;
	return 0;
}

代码优化：

基于vector二维向量的内存空间动态开辟，优化了自定义数据类型 Mat 的初始化操作。

#include <iostream>
#include <cstring>
#include <vector> 
#define MOD 1000000007
#define ZERO_MAT 0
#define IDENTITY_MAT 1
#define UNIT_MAT -1 //本题使用的0行0列为0，其他为1的原始矩阵 
using namespace std; 
/* run this program using the console pauser or add your own getch, system("pause") or input loop */

typedef vector<vector<int> > Mat; //定义基本数据类型 
const int op[7] = {0,4,5,6,1,2,3}; //定义骰子的对立面 
int d[7] = {0,1,1,1,1,1,1};

Mat Init(int rows,int cols,int type = IDENTITY_MAT)
{
	//开辟内存空间 
	Mat m(rows,vector<int>(cols));
	//赋值
	switch(type)
	{
		case -1://原始矩阵 
		
			for(int i = 0; i < rows; i++) m[i][0] = 0;
			for(int j = 0; j < cols; j++) m[0][j] = 0;
			for(int i = 1; i < rows; i++)
				for(int j = 1; j < cols; j++)
					m[i][j] = 1;
			break;
			
		case 0://零矩阵 
		
			for(int i = 0; i < rows; i++)
				for(int j = 0; j < cols; j++)
					m[i][j] = 0;
			break;
			
		case 1://单位矩阵
		
			 for(int i = 0; i < rows; i++)
				for(int j = 0; j < cols; j++)
				{
					if(i == j) 
						m[i][j] = 1;
					else
						m[i][j] = 0;
				}
			break;
			
		defalut://单位矩阵
			for(int i = 0; i < rows; i++)
				for(int j = 0; j < cols; j++)
				{
					if(i == j) 
						m[i][j] = 1;
					else
						m[i][j] = 0;
				} 
			break;
	} 
	return m;
}


//两个矩阵相乘  
Mat mul(Mat & a, Mat & b)
{
	Mat t;
	t = Init(a.size(),b[0].size(),0);//临时矩阵 
	 
	for(int i = 0; i < 7; i++)
		for(int j = 0; j < 7; j++)
			for(int k = 0; k < 7; k++)
				t[i][j] += (a[i][k] * b[k][j])%MOD;//t[i][j]:记录i行j列对应项相乘的和	
	return t;
}
// 向量和矩阵相乘 
int mul_d(Mat &a)
{
	int cols = a[0].size();
	int temp= 0;
	for(int j = 0;j < cols; j++)
	{
		for(int k = 0; k < cols; k++)
			temp += (d[k] * a[k][j])%MOD;	
		//cout<<temp<<endl; 
	}
	return temp;
}
//输出矩阵mat
void print_mat(Mat mat)
{
	int rows,cols;
	rows = mat.size();
	cols = mat[0].size();
	for(int i = 0; i < rows; i++)
	{
		for(int j = 0; j < cols; j++)
		{
			cout<<mat[i][j]<<" ";
		}
		cout<<endl;
	 } 
	 cout<<endl;
} 
int main(int argc, char** argv) {
	
	//初始化0行0列为0，其他为1的原始矩阵
	Mat mat;
	mat = Init(7,7,-1);
	//print_mat(mat);
	//输入骰子数和互斥对数 
	int n,m;
	cin>>n>>m;
	//逐行输入互斥对，完善互斥矩阵 
	int a,b; 
	for(int i = 0; i < m; i++)
	{
		cin>>a>>b;
		mat[a][op[b]] = 0;
		mat[b][op[a]] = 0; 
	}
	cout<<"mat = "<<endl;
	//print_mat(mat);
	//声明并初始化为单位矩阵 
	Mat E;
    E = Init(7,7);
	//print_mat(E);
	
	//求变换矩阵的n-1次方 
	int beishu = 4;
    while(n > 1)
    {
    	E = mul(E,mat);
    	//print_mat(E);
    	beishu *= 4;
    	n--;
	}
	//cout<<"n-1次连乘之后 E="<<endl;
	//print_mat(E);
	//情况总数ans = d[] * m的n-1次方 * 4的n次方 
	int ans = mul_d(E) * beishu;
	cout<<"ans = "<<ans<<endl;
	return 0;
}