HDU-1915-Knight Moves（双向BFS）

Knight Moves
Time Limit: 1000MS Memory Limit: 30000K
Total Submissions: 25071 Accepted: 11863
Description

Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
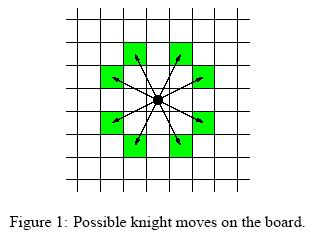
For people not familiar with chess, the possible knight moves are shown in Figure 1.

Input

The input begins with the number n of scenarios on a single line by itself.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first line specifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. The second and third line contain pair of integers {0, …, l-1}*{0, …, l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
Output

For each scenario of the input you have to calculate the minimal amount of knight moves which are necessary to move from the starting point to the ending point. If starting point and ending point are equal,distance is zero. The distance must be written on a single line.
Sample Input

3
8
0 0
7 0
100
0 0
30 50
10
1 1
1 1
Sample Output

5
28
0
Source

题意：首行给出T，代表有T组数据，每组数据先给出N代表有N*N的棋盘，注意下标是0~N-1，接着给出起点和终点坐标，按照马走日的规则，从起点走到终点最少需要多少步。

思路：起始状态和终止状态都知道，可以双向广搜。对于每一步，可以选择让起点走，也可以选择让终点走，那就根据已走步数的奇偶性，一替一步走，走之前判断自己现在的位置是不是被另一个自己走过，如果走过直接输出步数，走之后记录下自己走的位置，防止走回头路并方便另一个自己判断是否相遇。

代码

#include<stdio.h>
#include<iostream>
#include<algorithm>
#include<string.h>
#include<math.h>
#include<queue>
using namespace std;
//双向广搜
const int maxn=805;
const int INF=0x3f3f3f3f;
struct node
{
    int x;
    int y;
};
int N;//地图尺寸
int map_1[maxn][maxn];//标记起点走过的路
int map_2[maxn][maxn];//标记终点走过的路
int dis[8][2]= {{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
node star,endn;
bool Judge(node x)
{
    if(x.x>=0&&x.x<N&&x.y>=0&&x.y<N)
        return true;
    return false;
}
void BFS()
{
    map_1[star.x][star.y]=1;
    map_2[endn.x][endn.y]=1;
    queue<node>que[2];
    que[0].push(star);
    que[1].push(endn);
    int steap=0;//记录步数，同时根据奇偶性决定此步移动起点还是终点
    while(!que[0].empty()||!que[1].empty())//有一个队列不为空，就继续寻找交叉路径
    {
        int num=que[steap%2].size();
        while(num--)
        {
            star=que[steap%2].front();
            que[steap%2].pop();
            if((steap%2==0&&map_2[star.x][star.y]==1)||(steap%2==1&&map_1[star.x][star.y]==1))//两者路径有重合点
            {
                printf("%d\n",steap);
                return;
            }
            for(int i=0; i<8; i++)
            {
                endn=star;
                endn.x+=dis[i][0];
                endn.y+=dis[i][1];
                if(Judge(endn))//首先坐标要合法
                {
                    if(steap%2==0)//偶数步代表起点在走
                    {
                        if(map_1[endn.x][endn.y]==0)
                        {
                            que[steap%2].push(endn);
                            map_1[endn.x][endn.y]=1;
                        }
                    }
                    else//奇数步代表终点在走
                    {
                        if(map_2[endn.x][endn.y]==0)
                        {
                            que[steap%2].push(endn);
                            map_2[endn.x][endn.y]=1;
                        }
                    }
                }

            }
        }
        steap++;
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        scanf("%d",&N);
        for(int i=0; i<N; i++)
        {
            for(int j=0; j<N; j++)
            {
                map_1[i][j]=0;
                map_2[i][j]=0;
            }
        }
        scanf("%d%d%d%d",&star.x,&star.y,&endn.x,&endn.y);
        BFS();
    }
    return 0;
}